简介
戈特弗里德·威廉·莱布尼茨(Gottfried Wilhelm Leibniz,1646年7月1日-1716年11月14日),德国哲学家、数学家,是历史上少见的通才,被誉为十七世纪的亚里士多德。莱布尼茨在数学史和哲学史上都占有重要地位。
莱布尼茨与人为善,不说人家坏话。他相信,即使从最无知的人身上,也能学到东西。
他是帝王的高参,柏林科学院的第一任院长。是一位百科全书式的人物。
狄德罗曾这样评价莱布尼茨:当一个人将自己的才能和莱布尼茨比较时,就恨不得把所有的书都扔了,在世界上找个不起眼的地方躲起来,然后在那里安静地死去;莱布尼茨的思想是无序的死对头,任何最混乱的东西在他的心灵中也会变得井然有序;在他身上,两种几乎是无法相容的伟大品质融合在一起,这就是发现的精神和方法的精神。
莱布尼茨出生于莱比锡,父亲是大学教授,在其6岁的时候去世,为他留下一个私人图书馆,他每天沉溺于书海之中,并自学中、小学课程,12岁时自学拉丁文,并着手学习希腊文。14岁时进入莱比锡大学念书。莱布尼茨就酷爱读书,还自学了几门外语,15岁的时候就进入了莱比锡大学,学习数学,同时还钻研哲学和法学。
1666年.他想在莱比锡大学申请法学博士学位,但校方竟以他年龄太小而取消了他的资格。但临近的阿尔多夫大学接受了他的论文,授予他博士学位。所以仅仅20岁,他就获得了博士学位和教授席位。
1672年,莱布尼茨受派前往巴黎执行国家战略使命,并在巴黎居住了4年。他被邀请参加了数学团体。法国在数学领域当时居领先地位,已经出现了大名鼎鼎的笛卡尔、帕斯卡尔、惠更斯(Huygens)。莱布尼茨有幸结识感更斯,并对笛卡尔哲学有了直接的认识。
莱布尼茨是在大学学习欧几里得《几何原本》时,对数学产生浓厚兴趣的。
看样子很多高人从几何原本获得营养,比如牛顿,而我到了很老才知道这个事情,这是很可悲的教育体现。虽然我们初中学的基本都是欧式几何,但是对其哲学美没有感觉。不过,和前面谈到的那三位法国人一样,莱布尼茨也是在业余时间从事研究工作的。究其原因,17世纪的大学仅是教会的附庸,而哲学仍是神学的奴婢。与此同时,“大多数数学家处在亚里士多德的经院哲学阴影的笼罩之下,数学发展的动力来自于与学院相对抗的文艺复兴时期的人文学者”。
我们可以用笛卡尔来与莱布尼茨作一比较,两人都喜欢旅行,只不过前者以军人的身份,后者则作为政客的幕僚;前者在驻扎异国时萌生了解析几何的思想,后者是在肩负外交使命时完成了微积分学的发明,而他们取得这两项举世瞩目的成就时都不到而立之年。
在海牙,他见到了斯宾诺莎。由于与世界上最有数学天赋的知识分子相识,莱布尼茨蕴藏着的数学才华被激发了出来。1675一1676年间,他提出了”无穷小算法”,在巴黎期间,菜布尼茨还发明了一种能做加减乘除及开方运算的计算机,比帕斯卡尔仅能做加减的计算机有很大进步。
在哲学上,莱布尼茨的乐观主义最为著名;他认为,“我们的宇宙,在某种意义上是上帝所创造的最好的一个”。他和笛卡尔、巴鲁赫·斯宾诺莎被认为是十七世纪三位最伟大的理性主义哲学家。
莱布尼茨是德国历史上第一个拥有巨大影响的哲学家,他的思想对后来的德国哲学有巨大的直接的影响。是当之无愧的“德国哲学之父”。
对数学的贡献
莱布尼茨与艾萨克·牛顿各自独立发明了微积分,但是谁先发明微积分的争论是数学界至今最大的公案。
牛顿的粉丝德迪耶挑起的纷争(说莱布尼兹抄袭牛顿),莱布尼兹予以反驳,然后牛顿的更多粉丝介入,莱布尼兹的粉丝也介入。到后面莱布尼兹犯了一个错误,他向英国皇家学会起诉,试图结束这一争端。
然而牛顿此时是皇家学会的代理会长。
皇家学会受牛顿的操控,莱布尼兹没吃到什么好果子。他们不允许莱布尼兹为自己作证,而牛顿居于幕后煽风点火。牛顿认命了专门审查此事的委员会,事实上这些成员大多是牛顿的“粉丝”,最后委员会起草了关于调查的报告(这个报告大部分应该是牛顿所写)然后由皇家学会出版,他还写了拉丁文精简版发表在杂志上专门给欧洲人看。
1695年英国学者宣称:微积分的发明权属于艾萨克·牛顿;1699年又说:牛顿是微积分的“第一发明人”。1712年英国皇家学会成立了一个委员会调查此案,1713年初发布公告:“确认艾萨克·牛顿是微积分的第一发明人。
莱布尼兹最后潦倒的原因其实是他一直寄以厚望的汉诺威在做上英国国王后也不愿替他翻案,所以最后算是含恨而终。
在他死后,牛顿扬言他为伤透了莱布尼兹的心而洋洋得意。
12年后,牛顿在他的《自然哲学之原理》的新版本里做了一个小改动,以确保不能让莱布尼兹沾上一点他的光。
”莱布尼茨直至去世后的几年都受到了冷遇。由于对牛顿的盲目崇拜,英国学者长期固守于牛顿的流数术,只用牛顿的流数符号,不屑采用莱布尼茨更优越的符号,以致英国的数学脱离了数学发展的时代潮流。
我们来看看牛逼顿,虽然在物理上独树一帜,但是在人品以及思想上和莱布尼茨相差甚远,我们对比一下二人在微积分符号方面的优劣。
牛B顿大神定义的导数:

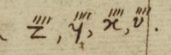
表示$z,y,x,v$的四次积分。且不说写起来如何,单就两个问题就很难回答:
- 这些导数对应的自变量是谁?
- 这些积分的积分变量又是谁?
一阶、二阶、三阶 …….n阶
\dot y %1个点
\ddot y %2个点
\dddot y %3个点
\ddddot y %4个点
\dot {\ddot y} %5个点
\ddot {\ddot y} %6个点
\dot{\ddot {\ddot y}} %7个点
\ddot{\ddot {\ddot y}}%8个点我顿悟了,latex下排版就是重新安排点的结构,这就是牛顿的标识方法,这种方式就是用最牛排版软件latex,都要动点脑筋才能打出来,更不要说满纸都是点了。
\ddddot{\ddddot{\ddddot{\ddddot{\ddddot{\ddddot{\ddddot{\ddddot{\ddddot{\ddddot{\ddddot{\ddddot{\ddddot{\ddddot{\ddddot{\ddddot{\ddddot{\ddddot{\ddddot{\ddddot{y}}}}}}}}}}}}}}}}}}}}%我设计了一个超级牛逼的输入方式,我自己都不知道有几个点!
https://cudl.lib.cam.ac.uk/view/MS-ADD-03962/17 牛顿手稿地址
牛B顿定义的偏导(注意:左边才是牛B顿的定义,中间是另外一位数学家Legendre定义的)
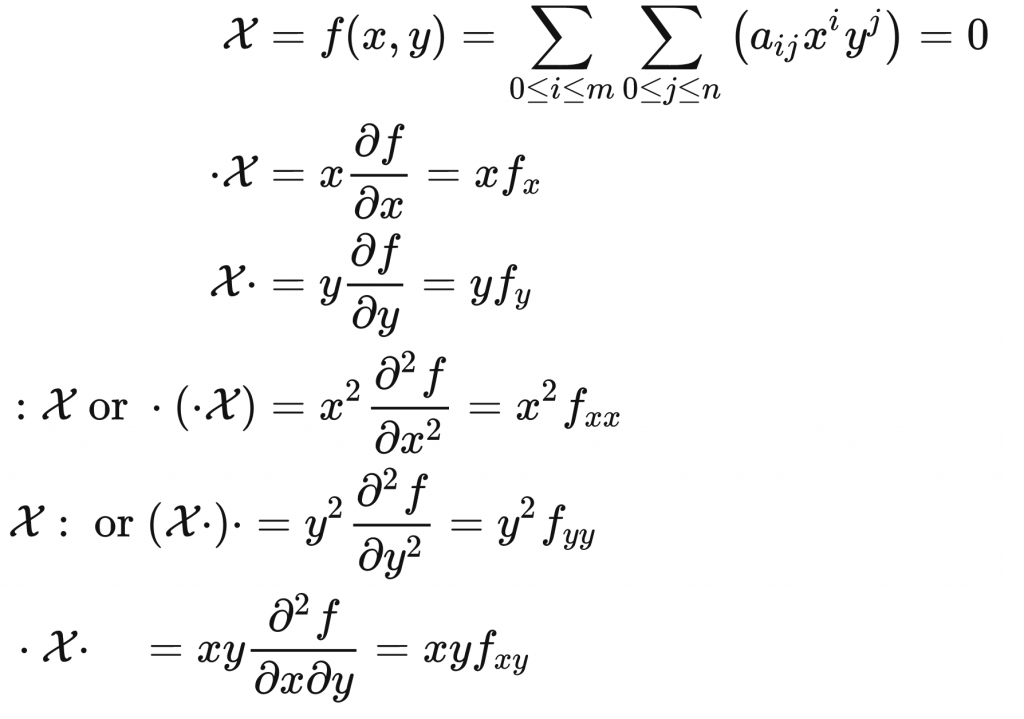
莱布尼茨的方式
一阶:$\dfrac{dx}{dy}$
n阶:$\dfrac{d^n x}{dx^n}$
再说牛顿的符号,处处透露着随意二字:
最魔性的也就在这一张手稿上:https://cudl.lib.cam.ac.uk/view/MS-ADD-03960/257
一筒到七筒
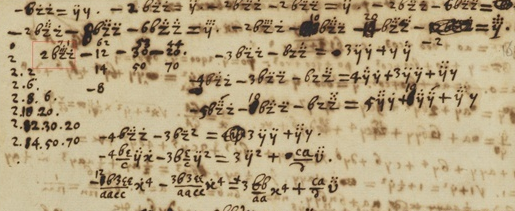

偏导的定义:

两点有时候表示“比”,但四点啥意思?联系了一下上下文,似乎就是除的意思。
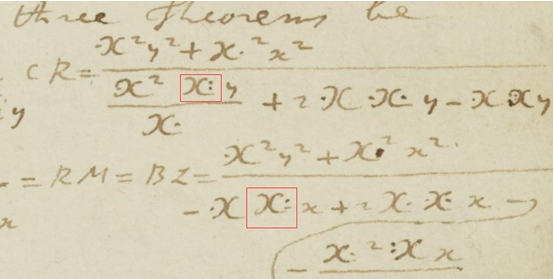
牛逼顿:我两点在$x$的弯弯里面就表示偏导,在弯弯外面就是除号 (“比例”),这只是几个例子有兴趣的可以可以自己去找手稿。
再符号方面牛顿和莱布尼茨真的差了很多,我和所有的学生都说,你需要细心才能做对题,但是提醒细心是没用的,只有改善制度才能让错误降低,显然,牛顿的模式如果流行,绝大多数的孩子将永远算不对,只有改善机制,才能让错误发的机会降低。
显然莱布尼茨要优秀的多。
莱布尼茨对数学问题的最早探索和最初贡献是试图沿着笛卡尔和霍布斯的思路建构所谓”通用语言”。这种语言是一种用来代替自然语言的人工语言,它通过字母和符号进行逻辑分析与综合,把一般逻辑推理的规则改变为演算规则,以便更精确更敏捷地进行推理。
为此,莱布尼茨做了两方面的努力:一是寻找能够代表所有概念并可认作最根本的不可分析的符号;二是给出表述诸如断定、合取、析取、否定、全称、特殊、条件联结等形式概念的设计。
关于第一方面,莱布尼茨首次设想用数目代表原初概念,而逻辑演算则用如同算术中的乘或除来代替。他认为用这种数字的不同方式排列组合,进行各种运算,就可产生无穷多的复合概念。这一思想后来改进为以素数代表基本概念,而复合词项即可借分解相应的数字成为它们的素数因子来加以分析。莱布尼茨又以设想的“人类概念字母表”为语言词汇基础创制了一些逻辑符号,如“∪”(并)、“∩”(交)等,一直沿用下来。
他的微积分领域的符号成为今天数学的通用符号,同时他的思想也广泛的被世界各个国家接受,并且促进了数学符号的统一。
很多英国数学家出于爱国的原因,拒绝接受莱布尼茨符号,因为狭隘的民族主义,英国数学界与欧洲大陆的数学界在近百年时间内缺乏交流,导致英国数学在黄金的十八世纪连一个伟大的数学家都没有。
直到1812年,巴贝吉、皮科克等人创立“剑桥分析学会”,旨在改革剑桥大学微积分的记号与教学状况,使英国数学研究出现转机。
莱布尼茨与中国文化
莱布尼茨是最早接触中华文化的欧洲人之一,曾经从一些曾经前往中国传教的教士那里接触到中国文化,之前应该从马可·波罗引起的东方热留下的影响中也了解过中国文化。
法国汉学大师若阿基姆·布韦(Joachim Bouvet,汉名白晋,1662-1732年)向莱布尼茨介绍了《周易》和八卦的系统。在莱布尼茨眼中,“阴”与“阳”基本上就是他的二进制的中国版。他曾断言:“二进制乃是具有世界普遍性的、最完美的逻辑语言”。今天在德国图林根,著名的郭塔王宫图书馆(Schlossbibliothek zu Gotha)内仍保存一份莱氏的手稿,标题写着“1与0,一切数字的神奇渊源。”
更进一步,二进制具有加减乘除运算,具有与其他进制的换算,而阴阳八卦根本没有加减乘除,与其他进制的换算。因此,它们仅仅具有表面的相似,本质上是不同的。
