先熟悉2个名词
1.真空介电常量
2.任意电介质介电常量
真空介电常量 $\varepsilon_{0}$,和引力常量G一样,也是一个常数。
库仑定律人人都知道,它是有试用条件的。
它只针对真空中静止的点电荷,静止两个字,先不管,请你注意真空两个字。
在真空中静电常量等于$k=9\times10^9$,这个数和引力常量$G=6.67×10^-11$一样,都是一个固定的值。
为了某些问题计算方便,我们把静电常量k,乘以4π,再取倒数,变成了真空介电常量。
$ \varepsilon_{0}=\frac{1}{4\pi k}$
$\varepsilon_{0}$叫做真空的介电常量.$ \varepsilon $ =$ 8.85×10−128.85\times10_{}^{-12}$ 。
所以真空介电常量也是一个常量,它是由静电常量k推导出来的,
所以库仑定律也可以写成$ F=\dfrac{Qq}{4\pi\varepsilon_{0}^{}r_{}^{2}} $这是对于真空,但是如果对于其他介质呢,比如,把两个带电小球放到油里面,通过实验发现,他们的静电力会衰减为真空的一定倍数,也就是说油中的k和真空的k不一样了,而且要小于真空的k。同理,$\varepsilon_{0}^{}$也不一样了,油中的ε要大于真空的$\varepsilon_{0}$。(k只有一个,不会变的,一般需要讨论ε,我们认为不同介质ε不一样)
举例来说,如果真空中的力为1N,放入油中的力变为0.5N,那么油中的ε一定就是真空的2倍,也就是$ε=2×8.85×10^{-12}=1.77×10^{-11}$
$1.77\times10^{-11} $叫做油的介电常量,但是我们不是经常使用,我们常用的是那个系数2,它叫做相对介电常量。比如,甘油的相对介电常量是45.8,它的意思是甘油中的介电常数为真空的45.8倍。
总结一下,现有真空静电常量k,由它导出真空介电常量$\varepsilon_{0}$,再乘以一定倍数变成某些物质的介电常量$\varepsilon$,
介电常数和温度、频率等都有关系,只是非常复杂已经不是高中能解决了。
对于高中 来说这些就足够!
| 材料 | 介电常数 (ε) |
| 真空 | 1.000 |
| 干燥的空气 | 1.0059 |
| 泡沫聚乙烯 | 1.6 |
| 含氟聚合物 | 2.0 |
| 聚丙烯 | 2.1 |
| 丁基橡胶 | 2.3 |
| 丁苯橡胶 | 2.9 |
| 硅橡胶 | 3.2 |
| 有机玻璃 | 3.4 |
| PVC | 4.0 |
| 玻璃 | 3.8-14.5 |
| 蒸馏水 | ~80 |
主要应用:
在生产收音机和其他电气设备中使用的电容器时使用材料。电路设计人员常用来比较不同的印刷电路板 (PCB) 材料。
此外,还可用于开发储能应用的材料,例如,聚合物基介电复合材料非常适合从电子封装、嵌入式电容器到能量存储的应用。这些复合材料在加工温度低的情况下具有高度的柔韧性,并且它们表现出相对高的介电常数、低介电损耗和高介电强度。
研究应用
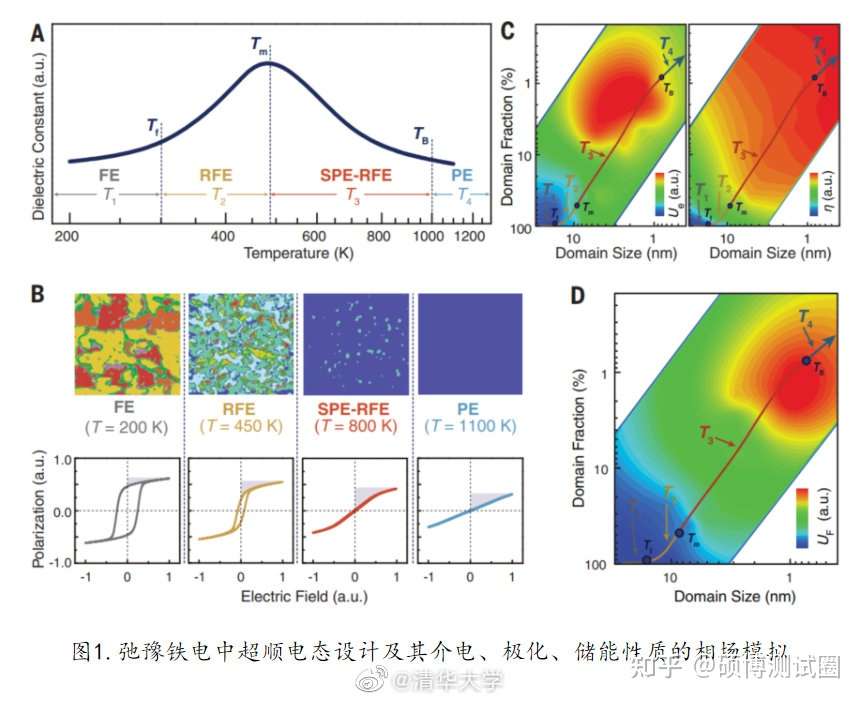
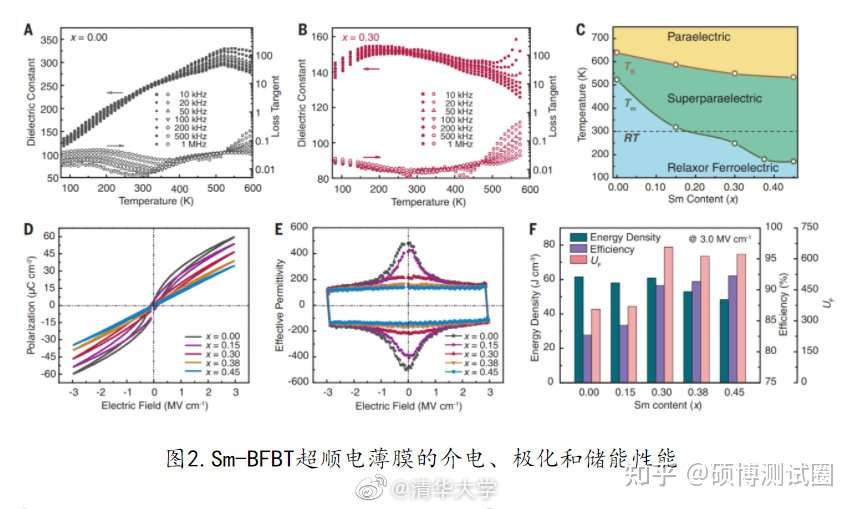
1.材料学院南策文院士、林元华教授研究团队在无铅储能介电材料研究中取得重要进展,通过对弛豫铁电薄膜材料的稳定的超顺电设计,实现了介电储能性能的显著提升。该成果可为下一代高端储能电容器提供关键材料和技术,也为介电新材料开发和其他基于弛豫铁电的功能优化提供了新的途径。
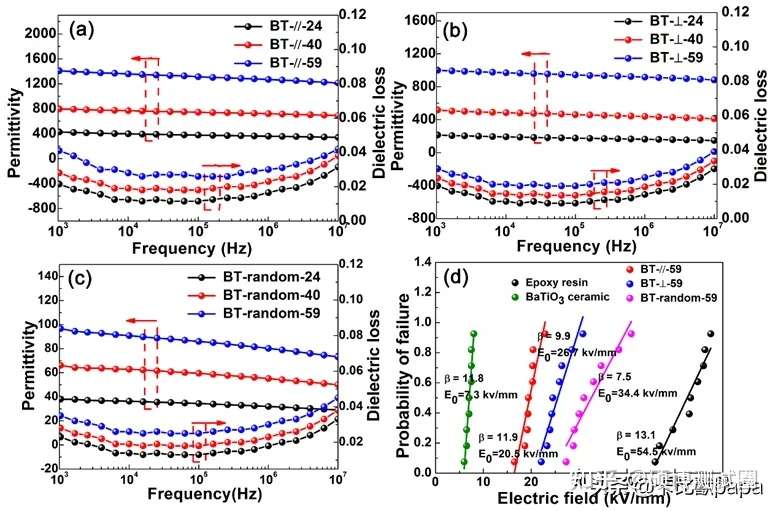
2.中南大学张斗教授课题组郭茹博士利用冷冻干燥成型及浸渍填充工艺制备了陶瓷相高度取向分布的BaTiO3/环氧树脂介电复合材料,该方法可实现材料成分、陶瓷含量、微观结构的有效调控。与传统方法得到的陶瓷填料颗粒无规分布的复合物相比,这种陶瓷颗粒定向排列的复合物由于电场耦合作用使得极化效应增强,进而获得了优异的介电性能(例如,在1kHz时,介电常数及损耗分别为1408和0.042),并在低工作电场下展现出显著提升的储能性能(相比于填料无规分布复合物,在6 kV/mm时,储能密度从3.0×10-2 J/cm3提高到19.6×10-2 J/cm3)。该工作为后续开发具有超高的介电常数和低介电损耗,具有良好的温度稳定性和抗疲劳性的轻质柔性电容器材料技术展现了良好的潜力和前景。