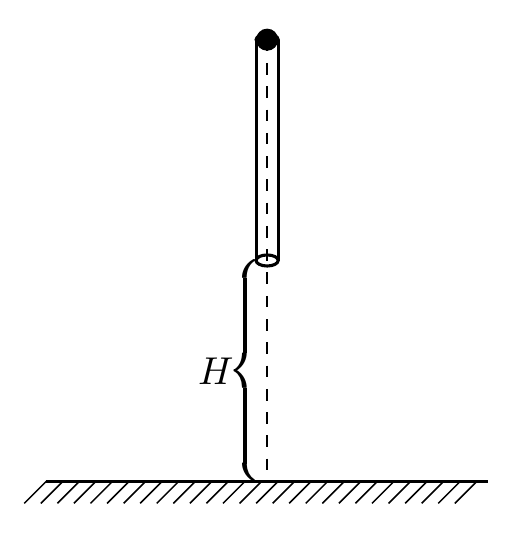
如图所示,一个质量为M长为L的圆管竖直放置,顶端塞有一个质量为m的弹性小球,M=4m,球和管间的滑动摩擦力和最大静摩擦力大小均为4mg.管从下端离地面距离为H处自由落下,运动过程中,管始终保持竖直,每次落地后向上弹起的速度与落地时速度大小相等,不计空气阻力,重力加速度为g.求:
(1)管第一次落地弹起时管和球的加速度;
(2)管第一次落地弹起后,若球没有从管中滑出,则球与管达到相同速度时,管上升的最大高度。
(3)管第二次弹起后球不致滑落,L应满足什么条件.
(1)管第一次落地弹起时,管瞬间向上运动,受到自身重力以及摩擦力,所以管的加速度$a_1=\frac{4mg+4mg}{4m}=2g$方向向下。球受到向上的摩擦力和向下的重力,球加速度$a_2=\frac{f-mg}{m}=\frac{4mg-mg}{m}=3g$方向向上。
(2)取竖直向下为正方向.球与管第一次碰地时速度$v_0=\sqrt{2gH}$ ,方向向下.碰地后管的速度$v_1=- \sqrt{2gH}$,方向向上;球的速度$v_2=\sqrt{2gH}$,方向向下若球刚好没有从管中滑出,设经过时间$t_1$,球管速度v相同,则有
$$-v_1+a_1t_1=v_2-a_2 {t_1}^2$$
$$-\sqrt{2gH}-2gt_1=\sqrt{2gH}+3mgt_1$$
$$2\sqrt{2gH}=5mgt_1$$
$$t_1=\frac{2}{5}\sqrt{\frac{2H}{g}}$$
此时管下端的高度为$h_1=v_0 t_1-\frac{1}{2} {a_1} {t_1}^2$ 带入数据
$$h_1=\frac{12}{25}H$$
此后管和球共速上升$v_g=v_0-a_2 t_1=\frac{1}{5} \sqrt{2gH}$
共速上升的高度 $$h_2=\frac{v_g ^2}{2g}=\frac{1}{25}H$$
管上升的最大高度$H_1$$$H_1=h_1+h_2=\frac{13}{25}H $$
(3)设第一次弹起过程中球相对于管的位移$x_1$,在管开始下落到上升到$H_1$的过程中,由动能减少量等于摩擦力做功
$$Mg(H-H_1+mg(H-h_1 + x_1)-4mg x_1=0$$
$$x_1= \frac{4}{5}H_1$$
即L应满足条件$x_1 +x_2 \leq L$
$$\frac{4}{5}H +\frac{4}{5}H_1\leq L$$
$$\frac{4}{5}H +\frac{4}{5} \frac{13}{25}H\leq L$$
$$\frac{152}{125}H\leq L$$
