用一把普通的尺子就可以测量地球的周长,你信吗?
没骗你,这是真的!
你只要学会一种诞生于2000多年前的酷炫的测量方法,就可以在几分钟内完成这个惊人的实验。不过这个方法虽然简单有效,却有一个限制条件——每年,它只在特殊的日子里才能奏效。
这个特殊的日子,就是夏至。
为何夏至如此特殊?
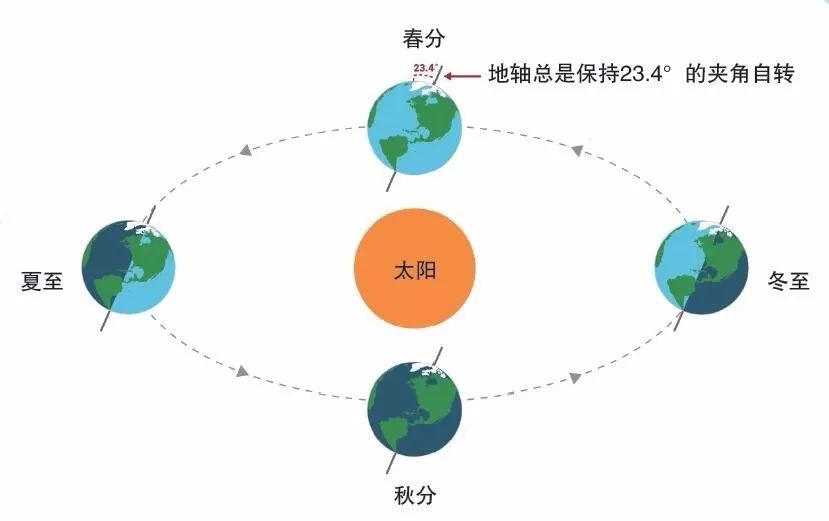
夏至是北半球一年里白昼时间最长的一天,正午时太阳在天空中“站”得最高。这是因为在夏至,太阳能直射的纬度几乎是一年中最靠北的,而且,地轴在这一天最大幅度地朝太阳倾斜。
埃拉托色尼和他的传奇故事
埃拉托色尼(公元前266—194年)是埃及亚历山大市的一位杰出的图书管理员,也是一位数学天才。我们有时会认为,在埃拉托色尼生活的时代,所有人都相信“天圆地方”。但这是个误会。当时受过教育的人其实已经知道地球是圆的,只是不知道这个“圆球”究竟有多大而已。
相传,埃拉托色尼无意中听说,在很远很远的地方,有一个名叫赛伊尼的小镇,当夏至这天到来时,正午的阳光会笔直地照进一口水井,不会在井底投下阴影,不仅如此,地面上所有的直立物体也都没有影子。
这个故事颠覆了埃拉托色尼此前的认知,因为在他的家乡亚历山大市,太阳照射的地方总会有影子。于是,他萌生了一个大胆的想法。

根据这个故事,量量地球有多“长”
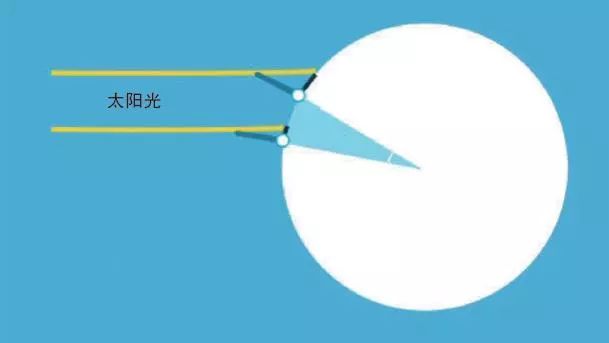
首先,埃拉托色尼画了一张图。他用一个圆来表示地球,用一组平行线来表示太阳的光线。这张图非常简单,看起来跟你在几何课上画得没什么两样。
埃拉托色尼发现,如果把地球看作一个西瓜,那么从亚历山大市切一刀,再从赛伊尼镇切一刀,就能切出一个薄片。接下来,只要知道整个“西瓜”有多少片这样大小的薄片,就可以通过“西瓜薄片”的弧长推出“西瓜”的周长。
“西瓜薄片”的弧长,其实就是亚历山大与位于赛伊尼的距离;“西瓜”里有多少个这样大小的薄片,可以通过计算亚历山大正午时太阳光线与地面的夹角得到。
接下来的计算
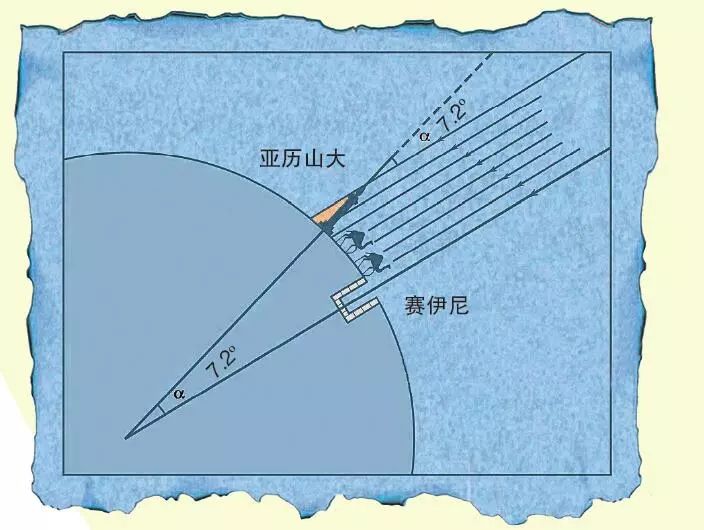
对埃拉托色尼这样的数学天才而言,计算光线与地面的夹角非常容易——只需测量一个竖直立柱在正午时的投影即可。立柱的高度和影子的长度构成直角三角形的两条直角边,斜边即为光线。而在直角三角形中,已知两条直角边的边长,就可以求出斜边与直角边的夹角。根据计算,埃拉托色尼得出这个夹角为7.2°。
但是测量亚历山大到赛伊尼的确切距离却非常困难。当时,人们想要估算两地之间的距离,通常要先计算骆驼车队从一个地方到另一个地方行进的速度,用速度与所用时间相乘,求得距离。但骆驼有时候是靠不住的,它们时快时慢,还可能走错路,所以这种计算方法不是很精确。据说,为了得到精确的距离,埃拉托色尼自掏腰包,让测量专家来“走”这段路,要求他们记录下全程的步数。最终,他得出这段距离约为800千米。
现在,埃拉托色尼已经知道了“西瓜薄片”的弧长,那么,“西瓜”里有几个这样大小的“西瓜薄片”呢?埃拉托色尼利用相似三角形的原理,推出从亚历山大和赛伊尼切下去的两刀之间的夹角也是7.2°(我们仍然用切西瓜来打比方)。所以,对整个“西瓜”来说,这样的薄片一共有360°/7.2°=50个。
了不起的壮举
埃拉托色尼计算出的地球周长为25000个视距。视距是一个古老的测量单位,1个视距相当于一个体育场的长度。如果转换为现代测量单位,大约是39590千米——这个数字与我们今天测量的40075千米惊人地接近。
有人说,这不还是有不小的误差嘛!别忘了,这里涉及视距与千米的单位换算。视距毕竟是以体育场的长度来定义的,而古代的体育场长度各异,所以很难将埃拉托色尼测量的数字准确转换为千米数。
不管怎么说,埃拉托色尼的这套方法非常科学,而且简便得让人不敢相信。毫无疑问,这是一项了不起的测量壮举。
现在,你也可以丈量地球了
准备好了吗?这可能是你在家里尝试过的“最大”的科学实验了!下面教你如何重复埃拉托色尼的实验。
你需要准备以下几样东西
尺子,
量角器,
铅笔,
纸。
一定要等到夏至这一天
这个实验只有在夏至当天才能做。夏至通常在6月20—22日到来,在2018年,这个日期是6月21日。正午时分,太阳“站”在天空最高处,这是测量的最佳时刻。但是需要强调的是,“正午”并不完全等同于中午12点哦,具体的测量时刻取决于你所在的地理位置,需要事先查好。
找到一个安全、平坦的平面,你就会看到投影。庭院、操场、野餐桌都是很好的选择。但要牢记基本的安全常识——千万不要直视太阳!
首先,找到光线与地面的夹角
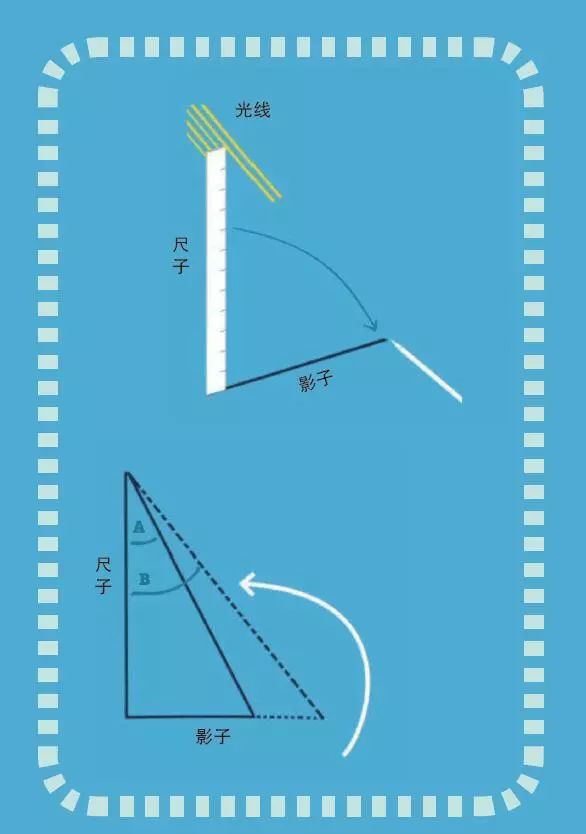
1. 把尺子直立起来,用铅笔标记下尺子的投影末端。
2. 把尺子放平,量出影子的长度。
3. 绘制图表。首先画一条与尺子长度相同的垂直线,然后,画出与你所测量的投影一样长的水平线。连接这两条线,形成一个直角三角形。
4. 用量角器测量斜边与竖直边的夹角,记为角A。
公式登场
等一下——那口起关键作用的水井去哪里找?在埃拉托色尼的实验中,他其实利用了正午时亚历山大的立碑和赛伊尼的水井的投影长度之差(只不过水井没有投影,所以长度为零而已)。但在你进行这项实验的时候,却无法得知哪里有这样一口水井,更无法准确测量你离那口井有多远。
还好,我们有备用计划。在夏至当天,邀请你远方的小伙伴一起来做这个实验吧!让他也按上面的步骤做一遍,把他测量的角度记为角B。
现在,把两个角度放入下面的公式,
【360 / (角B-角A)】×间距
在这里,“间距”是你和你小伙伴所在城市的距离,这可以通过查地图计算出来。由该公式得出的答案将是你对地球周长的估算。
多测几次,更准一点
所有实验都有误差,这个实验也不例外。夹角稍稍没测量准,就足以影响整个结果,测量时间和其他因素也会对结果产生影响。
尽管如此,只要你的答案中数字的位数正确(也就是数学家所说的“数量级正确”),就足以让你为自己感到骄傲——你丈量了地球!
我们不知道埃拉托色尼尝试了多少次。所以,在你的日历上标记好明年夏至的日期,那时你可以再做一次这个实验。
如果我错过了夏至怎么办?
如果夏至那天你一不小心忘记了测量,或者当天是个看不到太阳的阴雨天,那么你可以在夏至后的一两天的正午再试一次,这个实验仍然有效。
