正方形薄片电阻如图所示接在电路中,电路中电流为I,若在该电阻片中挖去一小正方形,挖去的正方形边长为原电阻片边长的三分之一,然后将带有正方形小孔的电阻片接在同一电源上,保持电阻片两端电压不变,电路中的电流变为多少?
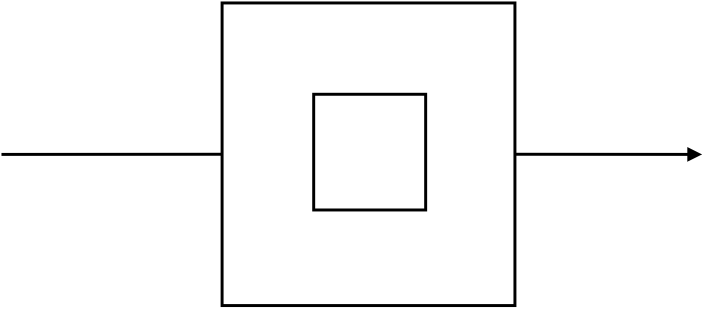
解法1、做物理常常需要构型,我们只需要几何形状把他看成一个个相等的电阻拼合即可。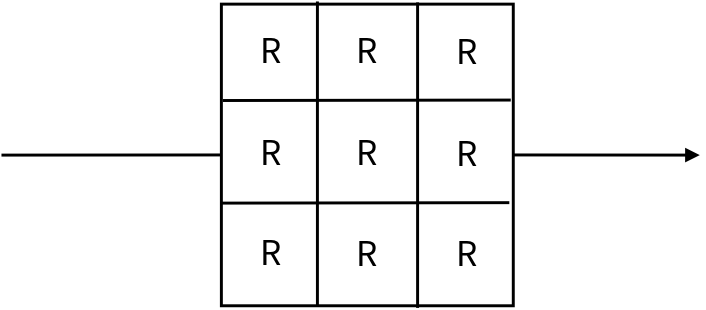
$${1\over R_1}={1 \over 3R} +{1 \over 3R}+{1 \over 3R}= {1\over R} $$
$$R_1=R$$
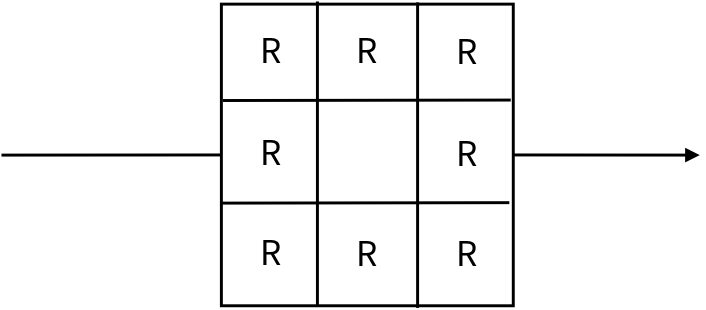
此时薄片相当于三个R的电阻并联、两个R电阻并联后再串联,三个R的电阻并联后的总电阻为R/3、两个R电阻并联后总电阻为R/2,则此时的总电阻.
$$ R_2 = {R \over 3} + {R \over 2} + {R \over 3} = {7R \over 6} $$
因正方形薄电阻片接在电路中,电路中电流为I,保持两端电压不变,U=IR
$$U = IR={I_2}{R_2}={I_2} {7R \over 6}$$
$$ I_2 = {6 \over7} {I} $$
解法2、当然这个题目还有一种接法,就是按照高中的公式,然后抽象画图形即可。 $$ R= \rho \frac {L}{S} $$
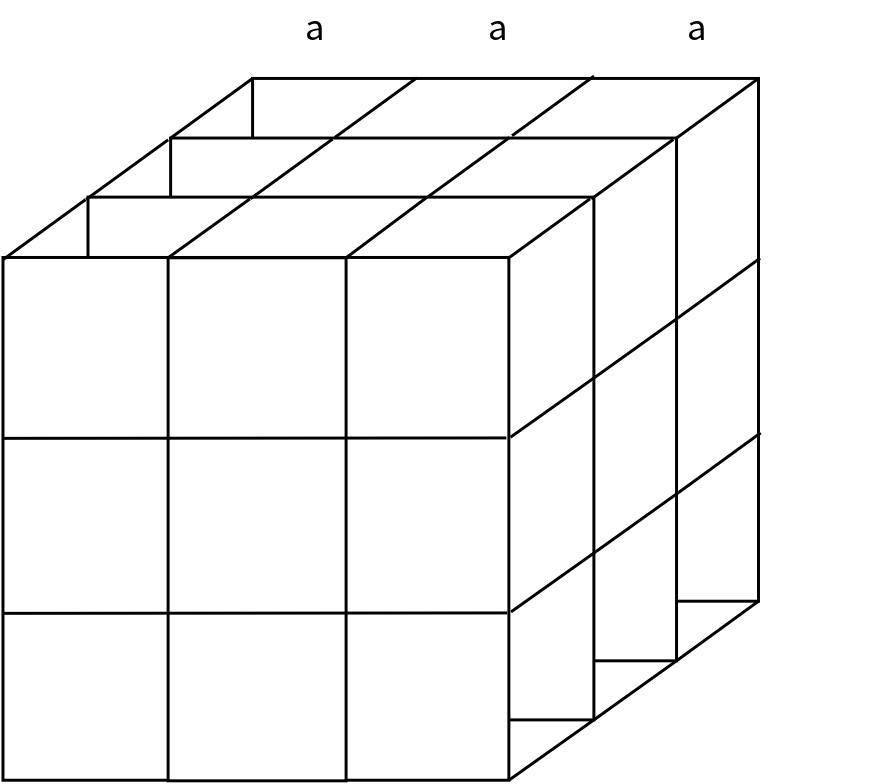
$$ R_1 =\rho \frac{3a}{9a^2}=\rho \frac{1}{3a} $$
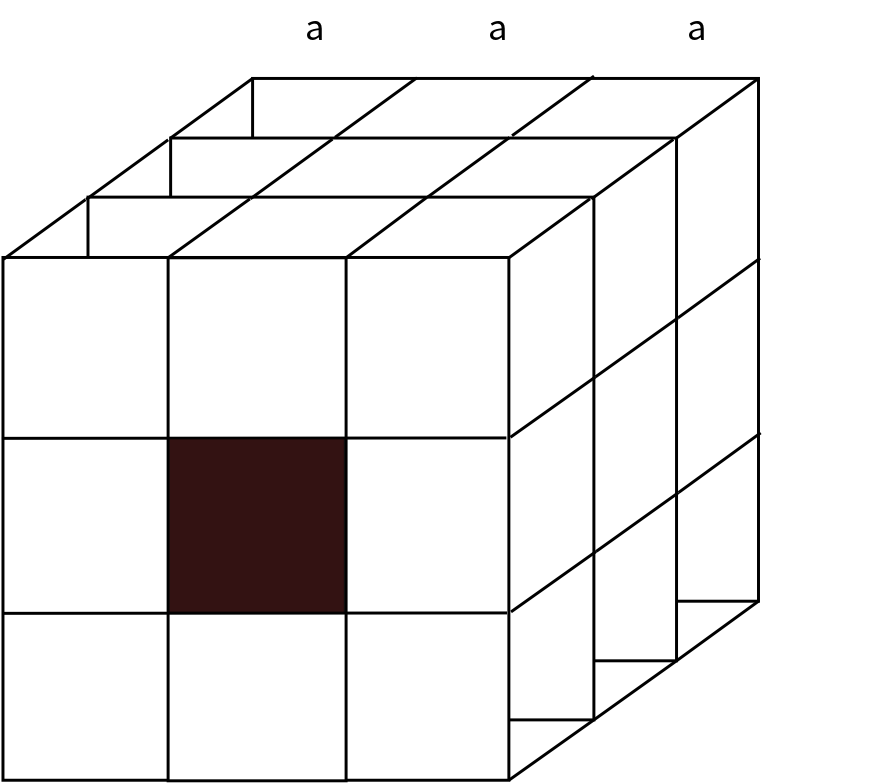
$$ R_2 = \rho \frac {a}{9a^2} +\frac {a}{6a^2} + \frac {a}{9a^2} =\rho \frac {7}{18a} $$
