静电场及其应用经典例题
如图所示,用等长绝缘线分别悬挂两个质量、电量都相同的带电小球A和B,两线上端固定于O点,B球固定在O点正下方。当A 球静止时,两悬线夹角为θ。能保持夹角θ不变的方法是( )
A.同时使两悬线长度减半
B.同时使A球的质量和电量都减半
C.同时使两球的质量和电量都减半
D.同时使两悬线长度和两球的电量都减半
展开答案
【答案】BD
【解析】设两球距离为d,分析A球的受力如图所示,图中$F=k\dfrac{q^2}{d^2}$。设绝缘线长度为L,由图中两个相似三角形关系可得:$\dfrac{mg}{L}=\dfrac{T}{L}=\dfrac{F}{D}$,即mg=T。由A球的受力矢量图可知,$2mgsin\dfrac{\theta}{2}=F=k\dfrac{q^2}{d^2}$。 同时使两悬线长度减半,则d减半,不能满足上式,选项A错误;同时使A球的质量和电量都减半,上式成立,选项B正确;同时使两球的质量和电量都减半,不能满足上式,选项C错误;同时使两悬线长度和两球的电量都减半, 则d、q1、q2减半,上式仍然能满足,选项D正确。
【扩展训练】
(多选) (2021·山东省等级考试第二次模拟)内半径为R,内壁光滑的绝缘球壳固定在桌面上。将三个完全相同的带电小球放置在球壳内,平衡后小球均紧靠球壳静止。小球的电荷量均为Q,可视为质点且不计重力。则小球静止时,以下判断正确的是( )
A. 三个小球之间的距离均等于R
B.三个小球可以位于球壳内任一水平面内
C.三个小球所在平面可以是任一通过球壳球心的平面
D.每个小球对球壳内壁的作用力大小均为$\frac{\sqrt{3}kQ^2}{3R^2}$,k为静电力常量
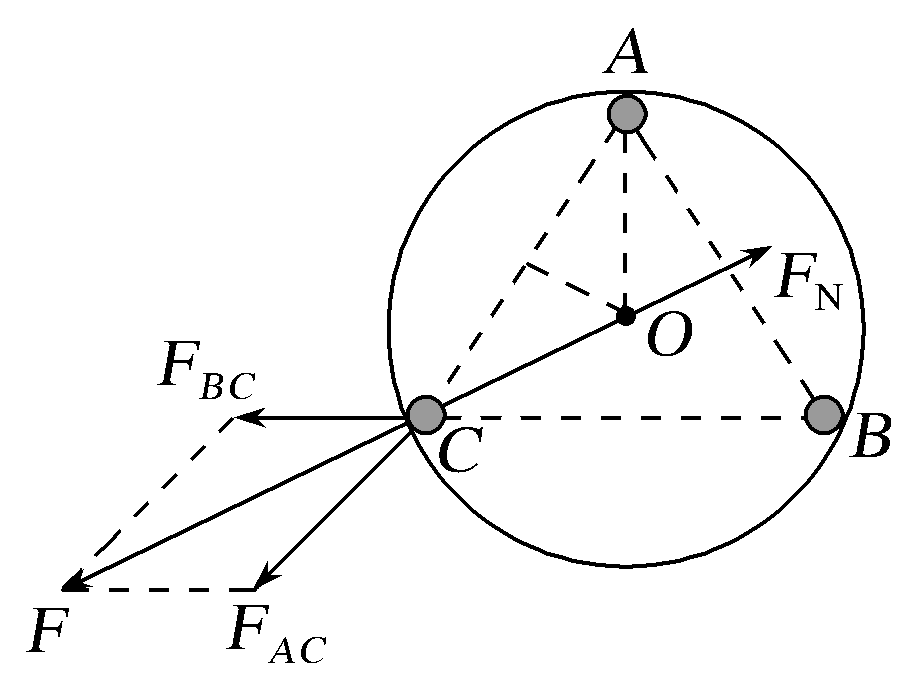
由库仑定律可知FAC=FBC=$k \frac{Q^2}{(\sqrt{3}R)^2}$=$\frac{kQ^2}{3R^2}$
其合力为F=2FACcos 30°=$\frac{\sqrt{3}kQ^2}{3R^2}$
【答案】CD
如图所示,以o 点为圆心的圆周上有六个等分点a、b、c、d、e、f。等量正、负点电荷分别放置在a、d 两点时,在圆心o 产生的电场强度大小为E。现仅将放于a 点的正点电荷改放于其他等分点上,使o 点的电场强度改变,则下列判断正确的是
A.移至c 点时,o 点的电场强度大小仍为E,沿oe 方向
B.移至b 点时,o 点的电场强度大小为$\frac{\sqrt{3}}{2}E$,沿oc 方向
C.移至e 点时,o 点的电场强度大小为$\frac{E}{2}$ ,沿oc 方向
D.移至f 点时,o 点的电场强度大小为$\frac{\sqrt{3}}{2}E$,沿oe 方向
展开答案
【解析】根据两个点电荷在0处电场强度的叠加,满足矢量合成的原理,进行分析即可,所以每个电荷产生的场强为$\frac{E}{2}$,所以选C,
答案:C
(多选)(2021·广东汕头市教学质量监测)质量均为m的三个带电小球A、B、C用三根长度均为l的绝缘丝线相互连接,放置在光滑绝缘的水平面上,A球的电荷量为+q。在C球上施加一个水平向右的恒力F之后,三个小球一起向右运动,三根丝线刚好都伸直且没有弹力,F的作用线的反向延长线与A、B间的丝线相交于丝线的中点,如图所示。已知静电力常量为k,下列说法正确的是( )
A.B球的电荷量可能为+2q
B.C球的电荷量为-2q
C.三个小球一起运动的加速度大小为$\dfrac{\sqrt{3}kq^2}{mL^2}$
D.三个小球一起运动的加速度大小为$\dfrac{2\times \sqrt{3}kq^2}{L^2}$
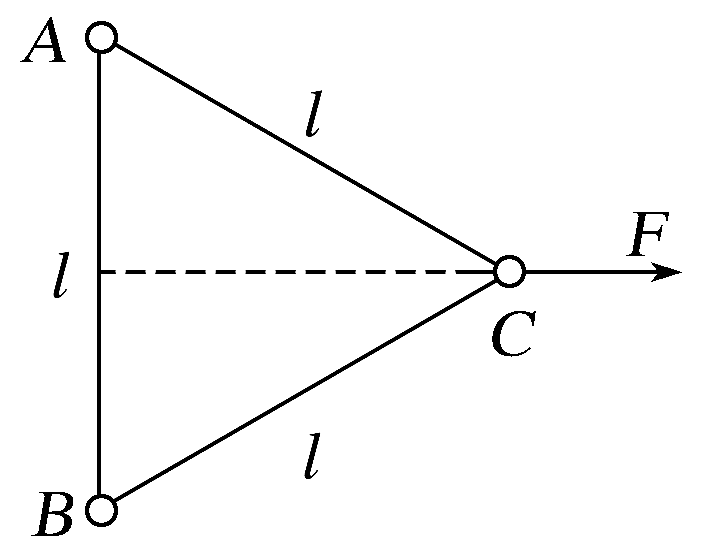
展开答案
【答案】BC
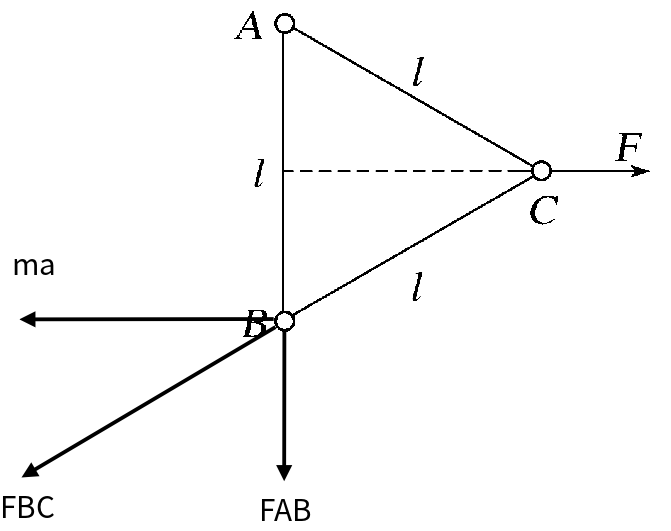
【解析】由题意可知小球运动的加速度方向与F 的作用线平行,则有:FBCsin 30°=FAB,FBCcos 30°=ma,解得:qC=2q,$\frac{\sqrt{3}kq^2}{mL^2}$,C 球带负电,故C 球的电荷量为-2q 故选【BC】
这题简单,但是我发现多数学生都不能快速准确的完成,主要是对加速的解读太多了。
力的分解只要几何形状确定,其中一个力确定,就可以顺藤摸瓜了,好比写程序,开始学习的时候要养成明确大致方向,然后简单的方式计算力,用制度解决粗心问题即可,养成良好的习惯会好很多。
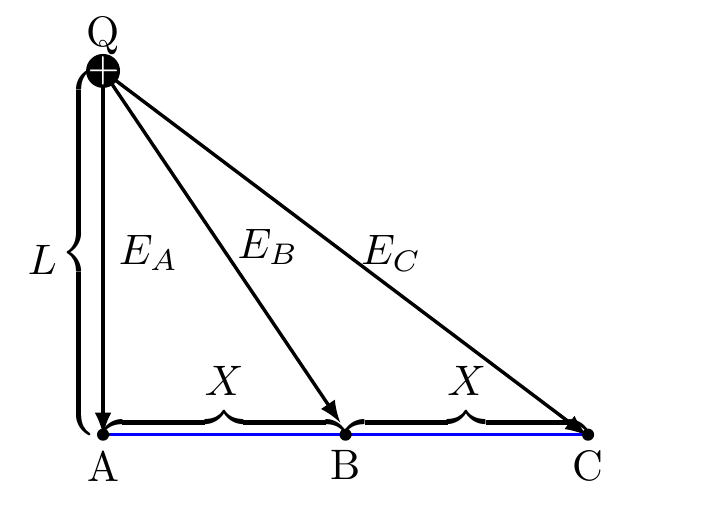
(2021·海南期末)真空中有一点电荷Q,MN是这个点电荷电场中的一条水平直线,如图所示,A、B、C是直线MN上的三个点,B是A、C的中点,点电荷Q位于A点正上方O处(未画出)。设A、B、C 三点场强大小分别为EA、EB、EC,且EB=$\frac{1}{2}$EA,则EC的值为( )
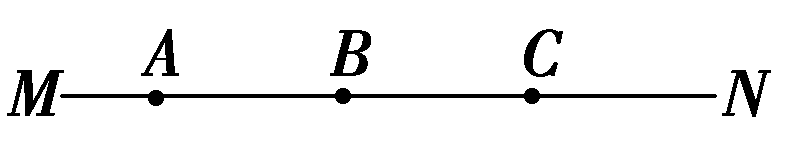
A.$\dfrac{1}{3}$EA B.$\dfrac{1}{4}$EA C.$\dfrac{1}{5}$EA D.$\dfrac{1}{6}$EA
展开答案
【答案】C
【解析】
这类题一定要注意草稿纸的格式,一眼看不出关系的,列方程组即可,但是方程组要写的整齐,这样一眼就能看出怎么解决问题。
设Q与A点的距离为L,Q与B点的距离为LB,Q与C点的距离为LC,
$E_B=\dfrac{1}{2}E_A$………..(1)
$E_A=\dfrac{kQ}{L^2}$………….(2)$\dfrac{1}{2}E_A=\dfrac{kQ}{2L^2}$
$E_B=\dfrac{kQ}{L^2+X^2}$……(3) $\dfrac{1}{2}E_A=\dfrac{kQ}{L^2+X^2}$
轻松得到:$2L^2=L^2+X^2$=>$L^2=X^2$
$E_C=\dfrac{kQ}{L^2+(2X)^2}$=>$E_C=\dfrac{kQ}{5L^2}=\dfrac{1}{5}E_A$
前两个简化一下
故选C。
(多选)(2021·云南大姚县一中一模)已知均匀带电球壳内部电场强度处处为零,电势处处相等。如图所示,正电荷均匀分布在半球面上,Ox为通过半球顶点与球心O的轴线,A、B为轴上的点,且AO=OB,则下列判断正确的是( )
A.A、B两点的电势相等
B.A、B两点的电场强度相同
C.点电荷从A点移动到B点,电场力一定做正功
D.同一个负电荷放在B点比放在A点的电势能大
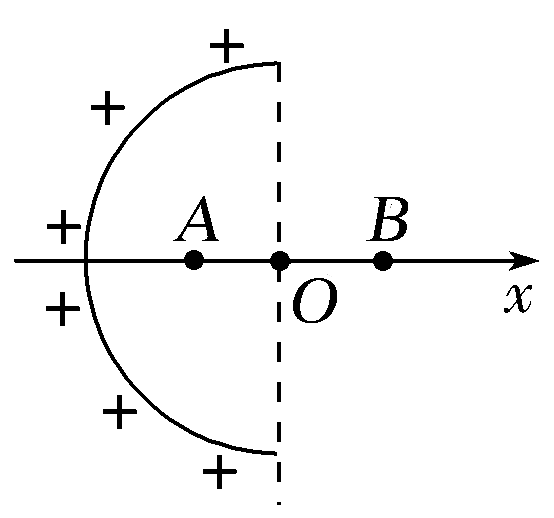
展开答案
【答案】BD
【解析】根据电场的叠加原理可知,x轴上电场线方向向右,则A点的电势高于B点的电势,故A错误;将半球壳补成一个完整的球壳,且带电均匀,设左、右半球在A点产生的场强大小分别为E1和E2。由题知,均匀带电球壳内部电场强度处处为零,则知 E1=E2。根据对称性可知,左、右半球在B点产生的场强大小分别为E2和E1,且 E1=E2。则在图示电场中,A的场强大小为E1,方向向右,B的场强大小为E2,方向向右,所以A点的电场强度与B点的电场强度相同,故B正确;点电荷从A点移到B点,电势降低,由于点电荷的电性未知,则电场力不一定做正功,故C错误;A点的电势高于B点的电势,根据负电荷在电势高处电势能小,在电势低处电势能大,知同一个负电荷放在B点比放在A点的电势能大,故D正确。故选BD
【扩展训练】
(2021·福建联考)均匀带电薄球壳在球外空间产生的电场等效于电荷集中于球心处产生的电场。如图所示,在半球面AB上均匀分布有正电荷,总电荷量为q,球面半径为R,CD为通过半球面顶点与球心O的轴线,在轴线上有M、N两点,OM=ON=2R。已知M点的场强大小为E,则N点的场强大小为( )
A.$\dfrac{kq}{4R^2}-E$ B.$\dfrac{kq}{4R^2}$ C.$\dfrac{kq}{2R^2}-E$ D.$\dfrac{kq}{2R^2}$
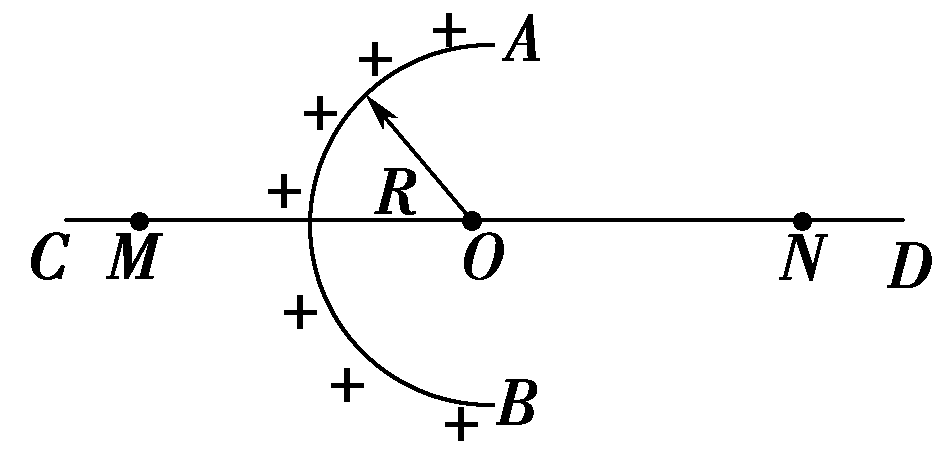
若将带电量为2q的球面放在O处,均匀带电的球壳在球外空间产生的电场等效于电荷集中于球心处产生的电场.则在M点所产生的电场为$E_{2Q}=\dfrac{kq}{2R^2}$,而将右侧去掉只剩左侧,M处的场强为E,说明右侧去掉部分在M处产生的场强为E′=$\dfrac{kq}{2R^2}-E$,根据对称性,左侧没去掉部分在右侧N点产生的场强也为$\dfrac{kq}{2R^2}-E$,故C 正确
如图所示,半径为R的绝缘闭合球壳,O为球壳的球心,球壳上均匀分布着正电荷,已知均匀带电的球壳在其内部激发的场强处处为零。现在球壳表面A处取下一面积足够小、带电量为q的曲面将其沿OA连线延长线向上移动至B点,且AB=R,若球壳的其他部分的带电量与电荷分布保持不变,下列说法中正确的是( )
A. 把另一带正电的试探电荷从A点处移动到O点过程中系统电势能减少
B. 球壳剩余部分的电荷在球壳内部激发的电场的电场线由A点的对称点C点沿直线指向球壳内表面各点
C. 球壳内部电场的电场线由球壳各点沿曲线指向A点
D. 球心O点场强的大小为$k\dfrac{3q}{4r^2}$
展开答案
【答案】CD
【解析】
根据题中“球壳上均匀分布着正电荷…取下一面积足够小、带电量为q的曲面…球壳剩余部分的电荷在球壳内部激发的电场…球壳内部电场的电场线”可知,根据电场强度的叠加规律,应用割补法、点电荷的场强特点、等量异种电荷的场强特点、电势能等知识分析求解。
B:球壳表面A处取下一面积足够小、带电量为q的曲面,相当于在球壳表面点A处放入等电荷密度、等面积的带负电荷的曲面。球壳剩余部分的电荷在球壳内部激发的电场可以看作两部分电荷电场的叠加,一部分是原球壳上均匀分布的正电荷在内部激发的电场,处处为零;另一部分是球壳上位于A处的等量负点电荷激发的电场,故球壳剩余部分的电荷在球壳内部激发的电场等同于只有A处的一个负点电荷激发的电场,如图(a)所示。故B项错误。
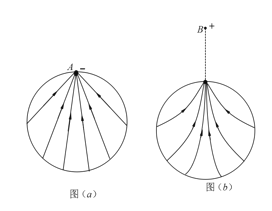
C:据B项分析可得,空间所有电荷在球壳内激发的电场相当于两个等量异种电荷产生的电场,如图(b)所示。故C项正确。
A:由图(b)知,带正电的试探电荷从A点处移动到O点,电势升高,电势能增加。故A项错误。
D:由C项分析知,球心O点场强大小$E_0=k\dfrac{q}{R^2}-k\dfrac{q}{(2R)^2}=k\dfrac{3q}{4R^2}$。故D项正确。
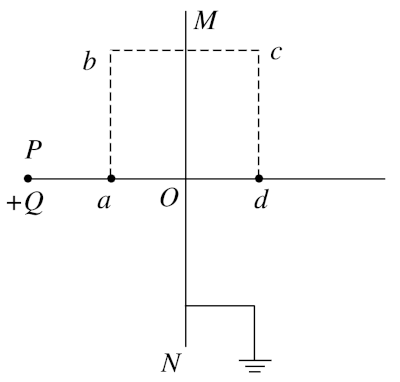
一无限大接地导体板MN前面放有一点电荷+Q,它们在周围产生的电场可看作是在没有导体板MN存在的情况下,由点电荷+Q与其像电荷-Q共同激发产生的.像电荷-Q的位置就是把导体板当作平面镜时,电荷+Q在此镜中的像点位置.如图所示,已知+Q所在位置P点到金属板MN的距离为L,a为OP的中点,abcd是边长为L的正方形,其中ab边平行于MN.静电力常量为k,则( )
A.a点的电场强度大小为$E=4K\dfrac{Q}{L^2}$
B.a点的电场强度大小大于b点的电场强度大小
C.b点的电场强度和c点的电场强度相同
D.一正点电荷从a点经b、c运动到d点的过程中电势能的变化量为零
展开答案
【答案】B
【解析】由题意可知,点电荷+Q和金属板MN周围空间电场与等量异种点电荷产生的电场等效,所以a点的电场强度
$$E=K \dfrac{Q}{\dfrac{L}{2}^2} + K \dfrac{Q}{\dfrac{3L}{2}^2} = \dfrac{40KQ}{9L^2} $$
A错误;等量异种点电荷周围的电场线分布如图所示,由图可知Ea>Eb,B正确;图中b、c两点的场强方向不同,C错误;由于a点的电势大于d点的电势,所以一正点电荷从a点经b、c运动到d点的过程中电场力做正功,电荷的电势能减小,D错误.
在光滑的水平面内有一沿x轴的静电场,其电势$\varphi$随x坐标值的变化图线如图所示。一质量为m,带电量为q的带正电小球(可视为质点)从O点以初速度$V_0$沿x轴正向移动。下列叙述正确的是( )
A.若小球能运动到$x_1$处,则该过程小球所受电场力逐渐增大
B.带电小球从$x_1$运动到$x_3$的过程中,电势能先减小后增大
C.若该小球能运动到$x_4$处,则初速度$v_0$至少为$2\sqrt{\frac{q {\varphi} _0}{m}}$
D.若$v_0=2\sqrt{\frac{q {\varphi} _0}{m}}$带电粒子在运动过程中的最大速度为$v_0=\sqrt{\frac{6q {\varphi} _0}{m}}$
展开答案
【答案】D
【解析】A.由于φ-x图象的斜率等于电场强度,则可知小球从O运动到x1的过程中,场强不变,由F=qE知,粒子所受电场力保持不变,故A错误;
B.正电荷在电势高处电势能大,则小球从x1运动到x3的过程中,电势不断减少,正电荷的电势能不断减少,故B错误;
C.若小球恰好能运动到x1处,初速度v0最小,从x=0到x1处,根据动能定理得
$-q{\varphi} _0=0-\dfrac{1}{2}m{v_0}^2$
得$\sqrt{\dfrac{2q {\varphi} _0}{m}}$故C错误;
当带电粒子运动到x3处时,电场力做正功最大,粒子的速度最大,从x=0到x3处,根据动能定理得
$q {\varphi} _0=\dfrac{1}{2}m{v_m}^2-\dfrac{1}{2}m{v_0}^2$
由题意${v_0}=2\sqrt{\frac{q {\varphi} _0}{m}}$,得最大速度为
$\sqrt{\dfrac{6q {\varphi} _0}{m}}$故D正确
(多选)一匀强电场的方向平行于xOy平面,平面内a、b、c三点的位置如图所示,三点的电势分别为10V、17V、26V.下列说法正确的是( )
A. 电场强度的大小为2.5V/cm
B. 坐标原点处的电势为1 V
C. 电子在a点的电势能比在b点的低7eV
D. 电子从b点运动到c点,电场力做功为9eV
展开答案
【答案】ABD
【解析】如图所示,在ac连线上,确定一b′点,电势为17V,将bb′连线,即为等势线,那么垂直bb′连线,则为电场线,再依据沿着电场线方向,电势降低,则电场线方向如下图,
因为匀强电场,则有:$E=\dfrac{U_{cb}}{d}$
依据几何关系,则$d=\dfrac{b’c×bc}{bb’}=\dfrac{4.5×6}{\sqrt{4.5^2+6^2}} =3.6cm$,
因此电场强度大小为$E=\dfrac{26−17}{3.6}=2.5V/cm$,故A正确;
B、根据φc-φa=φb-φo,因a、b、c三点电势分别为φa=10V、φb=17V、φc=26V,解得:原点处的电势为φ0=1 V,故B正确;
C、因Uab=φa-φb=10-17=-7V,电子从a点到b点电场力做功为W=qUab=7 eV,因电场力做正功,则电势能减小,那么电子在a点的电势能比在b点的高7 eV,故C错误;
D、同理,Ubc=φb-φc=17-26=-9V,电子从b点运动到c点,电场力做功为W=qUbc=9 eV,故D正确;
故选:ABD.
(多选)(2020·全国卷Ⅱ,20)如图,竖直面内一绝缘细圆环的上、下半圆分别均匀分布着等量异种电荷。a、b为圆环水平直径上的两个点,c、d为竖直直径上的两个点,它们与圆心的距离均相等。则( )
A.a、b两点的场强相等 B.a、b两点的电势相等
C.c、d两点的场强相等 D.c、d两点的电势相等
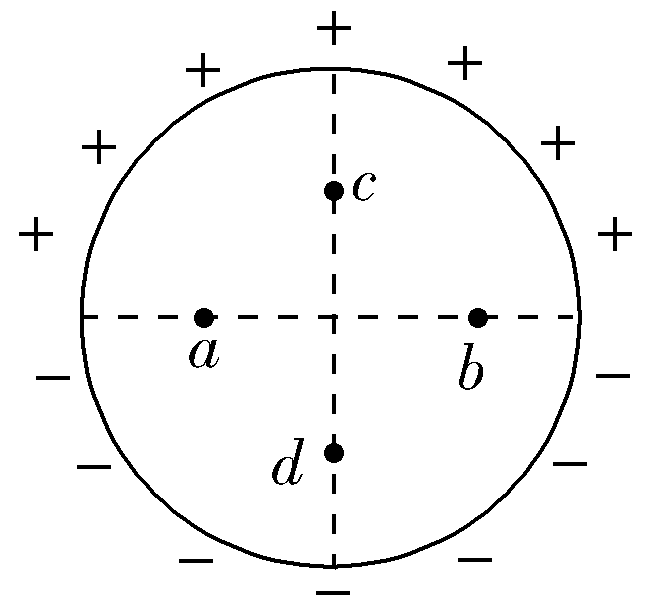
展开答案
【答案】ABC
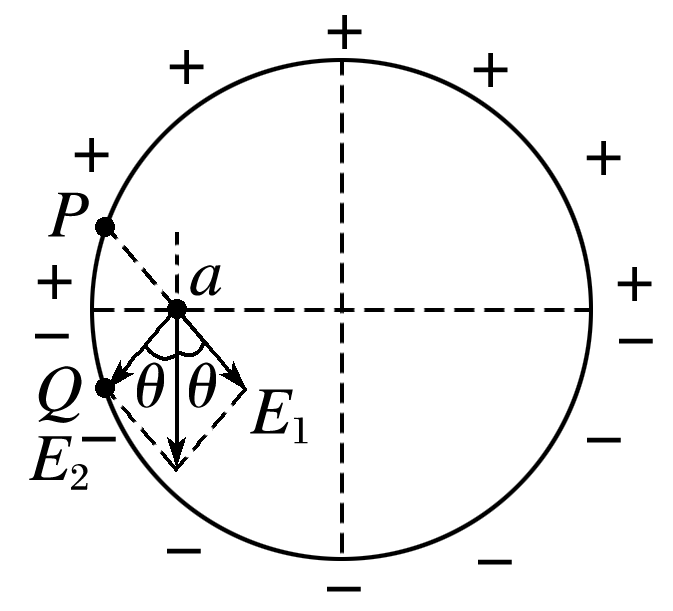
【解析】在绝缘细圆环的上半圆P处,任取一小段,可看成点电荷,其在a点产生的场强为E1,在P关于细圆环水平直径对称的下半圆Q处再取一小段,其在a点产生的场强为E2,由对称性可知,E1、E2的合场强竖直向下,如图所示,即上半圆和下半圆在a点产生的合场强一定竖直向下.同理可得,b点场强方向也竖直向下,由于a、b两点关于圆心对称,则b点处场强大小与a点处相等,故A正确;同理可分析a、b所在的直径上各点场强均竖直向下,故a、b两点在同一条等势线上,电势相等,故B正确;由微元法和对称性可知,c、d两点场强相等,方向竖直向下,故C正确;在c、d点所在直径上,电场方向由c到d,c点电势高于d点电势,故D错误.
[\toggle]
(上海交通大学自主招生)两个半径相同的金属球A、B带等量同种电荷,它们之间的距离远大于小球本身直径。已知它们相隔一定距离时,两球之间的相互作用力的大小是F,现在用一个带有绝缘柄的原来不带电的半径相同的金属小球C,先与小球A接触,再和小球B接触后移开。这时,A、B两球之间的相互作用力大小变为
A.F/2 B.F/4
C.3F/4 D.3F/8
[toggle]
答案:D
解析:根据库仑定律,金属球A、B之间的库伦力正比于金属球A、B带电量的乘积,即F=kQ2/r2。设开始时金属球A、B带电量均为Q,金属小球C与小球A接触后,二者平分,各自带电量Q/2。金属小球C再与小球B接触后,二者平分,各自带电量(Q+Q/2)/2=3Q/4。这时二者带电量的乘积为Q/2·3Q/4=3Q/8。所以A、B两球之间的相互作用力大小变为3F/8。选项D正确。
如图所示,一圆环上均匀分布着正电荷,x轴垂直于环面且过圆心O。下列关于x轴上的电场强度和电势的说法中正确的是( )
A.O点的电场强度为零,电势最低
B.O点的电场强度为零,电势最高
C.从O点沿x轴正方向,电场强度减小,电势升高
D.从O点沿x轴正方向,电场强度增大,电势降低
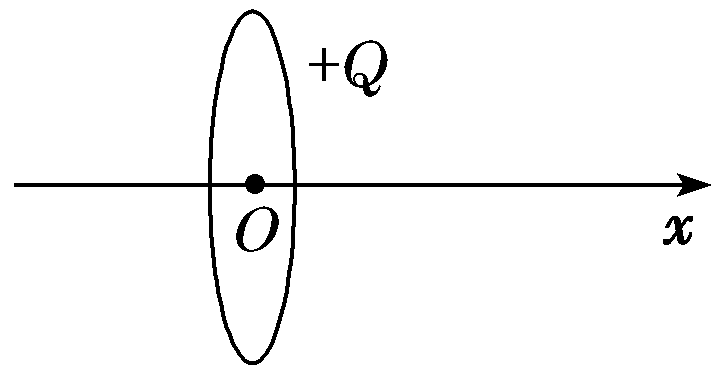
展开答案
【答案】B
【解析】将整个圆环看做由两个半圆环组成,由对称性可知,这两个半圆环上的电荷在O点的场强大小相等,方向相反,故合场强为零。x轴上的各点合场强,由对称性可知,在圆环右侧的合场强方向沿x轴向右,电势降低;左侧的合场强方向沿x轴向左,电势降低,故O点电势最高。由于在O点场强为零,距O点无限远场强为零,因此沿x轴向左、右两侧,电场强度都呈现出先增大后减小的特征,综上所述B正确。
如图所示,电荷均匀分布在半球面上,它在这半球的中心O处电场强度等于E.两个平面通过同一条直径,夹角为α,从半球中分出一部分球面,则所分出的这部分球面上(在“小瓣”上)的电荷在O处的电场强度为( )
A.E=Esinα
B.E=Ecosα
C.E=Esin$\dfrac{a}{2}$
D.E=Ecos$\dfrac{a}{2}$
展开答案
【答案】C
【解析】半球的中心O处电场强度E是部分球面上电荷产生的电场叠加的结果,根据对称性,作出球面上的电荷在O点产生的电场分布,由平行四边形定则求解“小瓣”球面上的电荷在O处的电场强度.
解:根据对称性,作出球面上的电荷在O点产生的电场分布,如图所示,由平行四边形定则得到“小瓣”球面上的电荷在O处的电场强度E=Esin$\dfrac{a}{2}
故选 C
点评:本题解题关键是抓住对称性,作出两部分球面上电荷产生的电场分布图.
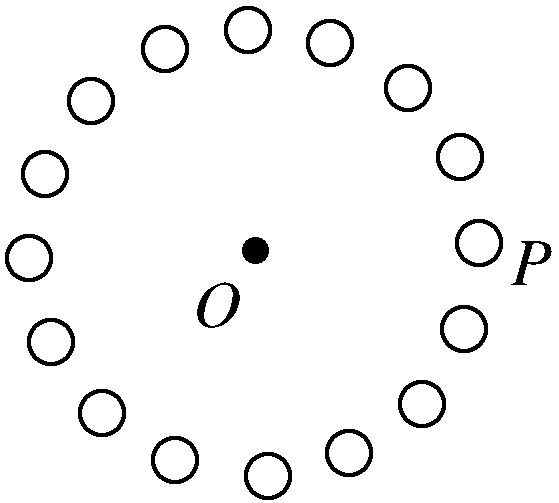
(2020·衡水模拟)如图所示,N(N>5)个小球均匀分布在半径为R的圆周上,圆周上P点的一个小球所带电荷量为-2q,其余小球带电量为+q,圆心处的电场强度大小为E。若仅撤去P点的带电小球,圆心处的电场强度大小为( )
A、$E$ B、$\dfrac{E}{2}$C、$\dfrac{E}{3}$D、$\dfrac{E}{4}$
展开答案
【解析】选
C 假设圆周上均匀分布的都是电荷量为+q的小球,由于圆周的对称性,圆心处场强为
0,则知在P处带电量+q的小球在圆心处产生的场强大小为$E_1=k\dfrac{q}{r^2}$,方向水平向左,可知圆周上其余小球在O处产生的场强大小为$E_2=E_1=k\dfrac{q}{r^2}$,方向水平向右,带电量为-2q的小球在圆心处产生的场强大小为$E_3=k\dfrac{2q}{r^2}$,方向水平向右。根据叠加原理E=E2+E3,则$k\dfrac{q}{r^2}=\dfrac{E}{3}$,所以撤去P点的小球后,圆心处场强大小为3,
C正确。
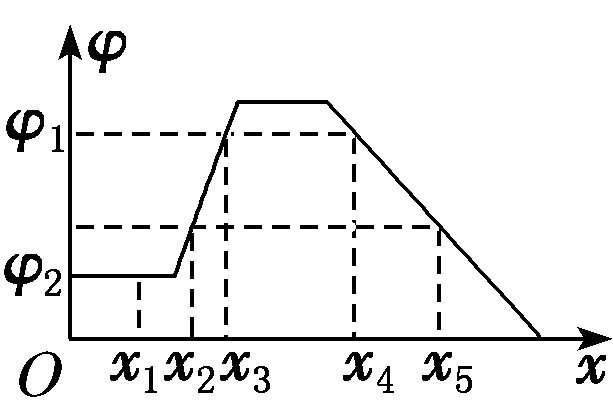
假设空间某一静电场的电势φ随x变化情况如图所示,根据图中信息可以确定下列说法中正确的是( )
A.O~x1范围内各点场强的方向均与x轴平行
B.只在电场力作用下,正电荷沿x轴从O运动到x1,可做匀减速直线运动
C.负电荷沿x轴从x2移到x3的过程中,电场力做正功,电势能减小
D.无法比较x2~x3与x4~x5间的场强大小
展开答案
解析】选
C 由图像可以知道,在O~x1范围内各点电势不变,是一条等势线,所以电场方向应该与x轴垂直,选项
A错误;在x轴上O~x1范围内,各点电势相等,任意两点间电势差为零,电场力做功为零,而且电荷做直线运动,可能做匀速运动,选项
B错误;负电荷沿x轴从x2移到x3的过程中电势升高,则电场力对负电荷做正功,电势能减小,选项
C正确;在x2~x3范围内相对于x4~x5范围内等差等势面密集,所以前者电场强度大些,选项
D错误。
(多选·洛阳模拟)空间有一沿x轴对称分布的电场,其电场强度E随x变化的图像如图所示,带电粒子在此空间只受电场力作用。下列说法中正确的是( )
A.在-x1处释放一带负电的粒子,它将沿x轴在-x1与x1之间做往返运动
B.带负电的粒子以一定的速度由-x1处沿x轴正方向运动到x1处,它在x1处的速度等于在-x1处的速度
C.带正电的粒子以一定的速度由-x1处沿x轴正方向运动的过程中,它的动能先增大后减小
D.带正电的粒子在x1处的电势能比在x2处的电势能小、与在x3处的电势能相等
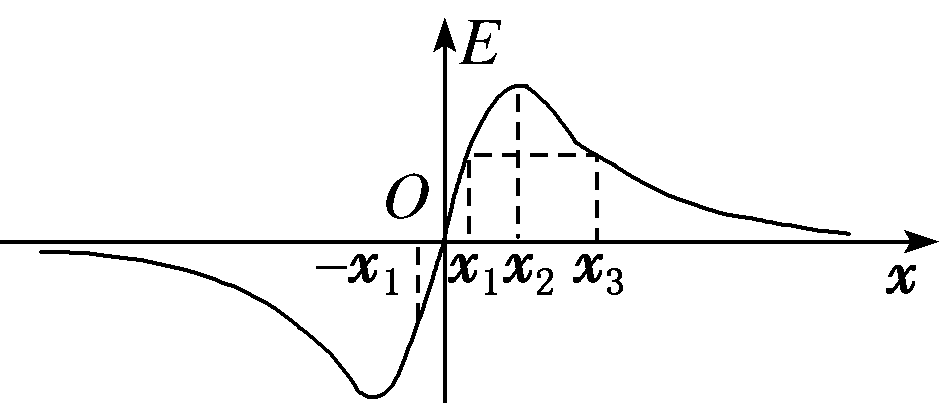
展开答案
【解析】选
AB 电场沿x轴对称分布,在-x1处释放一带负电的粒子,它将沿x轴在-x1与x1之间做往返运动,选项
A正确。带负电的粒子以一定的速度由-x1处沿x轴正方向运动到x1处,它在x1处的速度等于在-x1处的速度,选项
B正确。带正电的粒子以一定的速度由-x1处沿x轴正方向运动的过程中,它的动能先减小后增大,选项
C错误。从x1处到x3处,电场强度方向沿x轴正方向,带正电的粒子从x1处到x3处,电场力一直做正功,电势能减小,所以带正电的粒子在x1处的电势能比x2处的电势能大、比x3处的电势能大,选项
D错误。
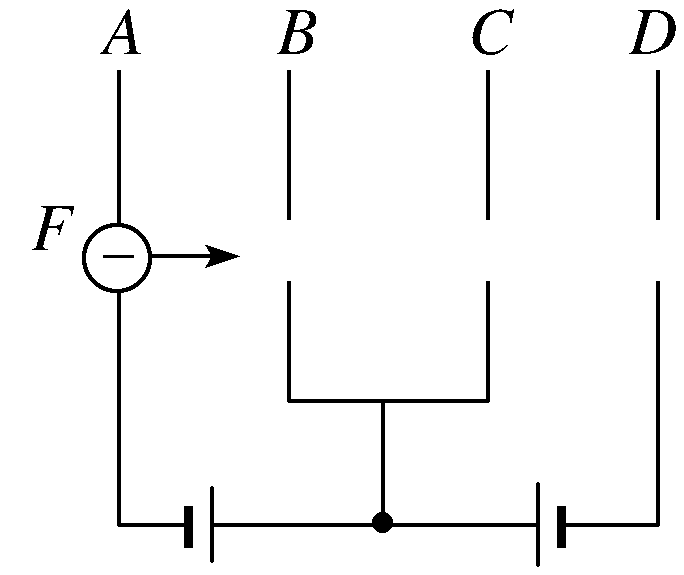
如图所示,从F处释放一个无初速度的电子向B板方向运动,指出下列对电子运动的描述中哪句是错误的(设电源电动势为U)( )
A.电子到达B板时的动能是Ue
B.电子从B板到达C板动能变化量为零
C.电子到达D板时动能是3Ue
D.电子在A板和D板之间做往复运动
展开答案
【解析】选
C 电子在A、B之间做匀加速运动,且eU=ΔEk,
A正确;在B、C之间做匀速运动,
B正确;在C、D之间做匀减速运动,到达D板时,速度减为零,
C错误,
D正确。
