静电场及其应用
一、电荷和电荷守恒定律
1.点电荷:形状和大小对研究问题的影响可忽略不计的带电体称为点电荷.
2.最小的带电单元,任何带电体的带电量都是元电荷的整数倍,e=1.6×10-19C——密立根 油滴实验测得e的值
3.电荷守恒定律
(1)电荷既不会创生,也不会消灭,它只能从一个物体转移到另一个物体,或者从物体的一部分转移到另一部分;在转移过程中,电荷的总量保持不变.
(2)起电方式:摩擦起电、接触起电、感应起电.
4.电流:电荷定向运动 $I=\frac{Q}{t}$
二、库仑定律
1.内容:真空中两个静止点电荷之间的相互作用力,与它们的电荷量的乘积成正比,与它们的距离的二次方成反比,作用力的方向在它们的连线上.
2.公式:
$$F=K \frac{q_1 q_2}{R^2}$$
式中$k=9.0×10^2 N·m^2/C^2$,叫做静电力常量.
3.适用条件:(1)点电荷;(2)真空.
三、电场强度
1.意义:描述电场强弱和方向的物理量, 矢量可以叠加计算方式同力。
2.公式
(1)定义式:$E=\frac{F}{Q}$,是矢量,单位:N/C或V/m.
(2)计算式:$E=K \frac{Q}{R^2}$,Q为场源电荷,r为某点到Q的距离.
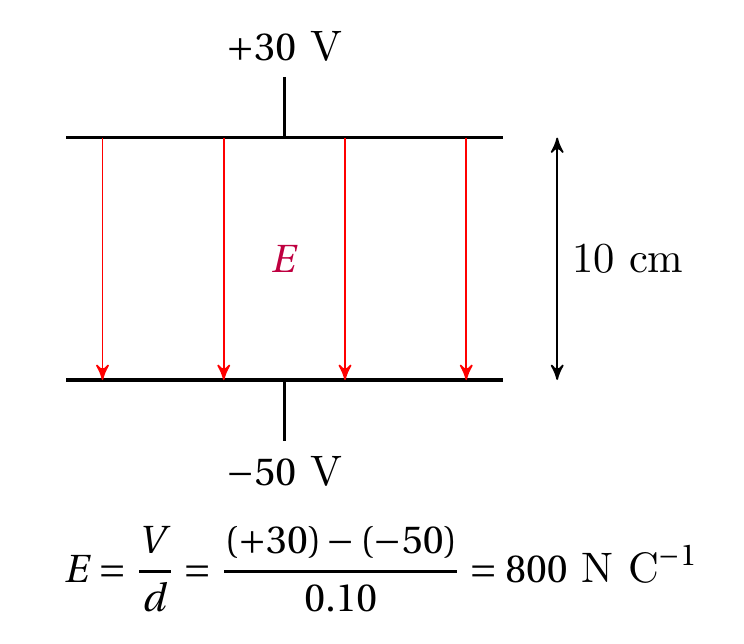
(3)匀强电场的场强:$E=\frac{U}{d}$.
3.方向:规定为正电荷在电场中某点所受电场力的方向.
四、电场线及特点
1.电场线:电场线是画在电场中的一条条有方向的曲线,曲线上每点的切线方向表示该点的电场强度方向.
2.电场线的特点
(1)电场线从正电荷或无限远处出发,终止于负电荷或无限远处.
(2)电场线不相交.
(3)在同一电场里,电场线越密的地方场强越大.
(4)沿电场线方向电势降低.
(5)电场线和等势面在相交处互相垂直.
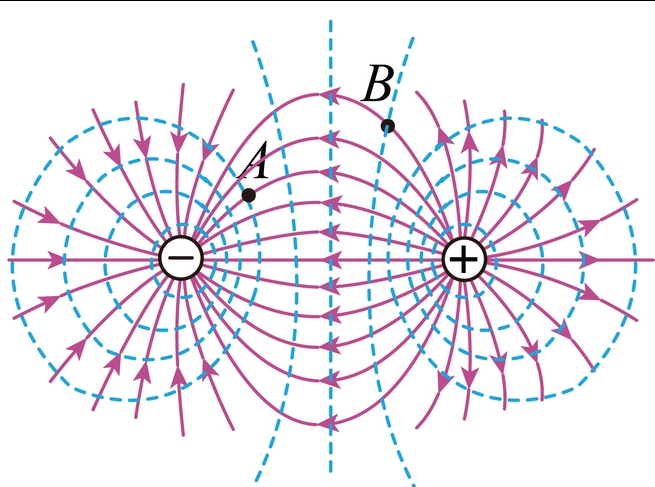
3.几种典型电场的电场线(如图所示)

4. 静电屏蔽
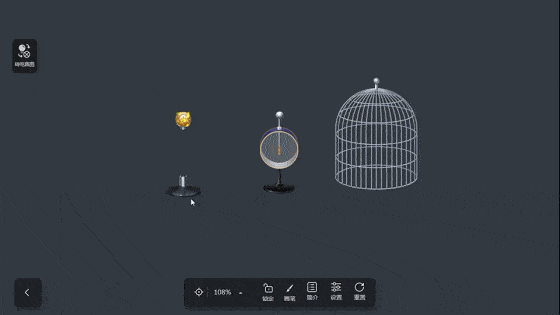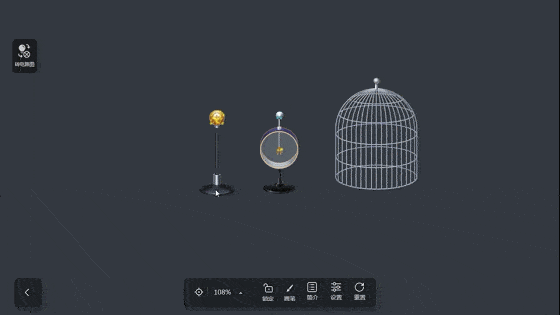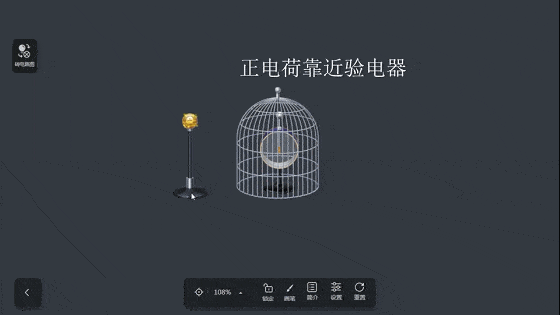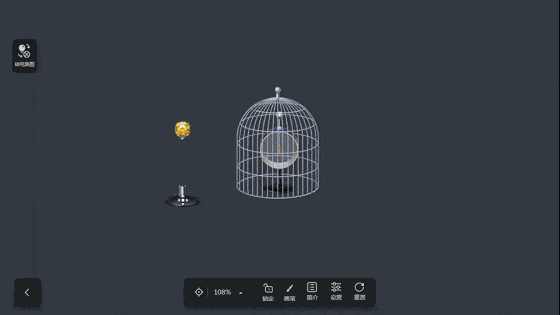
法拉第曾经冒着被电击的危险,做了一个闻名于世的实验——法拉第笼实验。法拉第把自己关在金属笼内,当笼外发生强大的静电放电时,什么事都没发生。
静电屏蔽:为了避免外界电场对仪器设备的影响,或者为了避免电器设备的电场对外界的影响,用一个空腔导体把外电场遮住,使其内部不受影响,也不使电器设备对外界产生影响,这就叫做静电屏蔽。空腔导体不接地的屏蔽为外屏蔽,空腔导体接地的屏蔽为内屏蔽。
在静电平衡状态下,不论是空心导体还是实心导体;不论导体本身带电多少,或者导体是否处于外电场中,必定为等势体,其内部场强为零,这是静电屏蔽的理论基础,同样很多功率较大,或者有高压电路的设备都是金属外壳的原因。
考点一 对库仑定律的理解和应用
1.对库仑定律的理解
(1)$F=K \frac{q_1 q_2}{R^2}$,r指两点电荷间的距离.对可视为点电荷的两个均匀带电球,r为两球心间距.
(2)当两个电荷间的距离r→0时,电荷不能视为点电荷,它们之间的静电力不能认为趋于无限大.
2.电荷的分配规律
(1)两个带同种电荷的相同金属球接触,则其电荷量平分.
(2)两个带异种电荷的相同金属球接触,则其电荷量先中和再平分.
考点二 电场线与带电粒子的运动轨迹分析
1.电荷运动的轨迹与电场线一般不重合.若电荷只受电场力的作用,在以下条件均满足的情况下两者重合:
(1)电场线是直线.
(2)电荷由静止释放或有初速度,且初速度方向与电场线方向平行.
2.由粒子运动轨迹判断粒子运动情况:
(1)粒子受力方向指向曲线的内侧,且与电场线相切.
(2)由电场线的疏密判断加速度大小.
(3)由电场力做功的正负判断粒子动能的变化.
3.求解这类问题的方法:
(1)“运动与力两线法”——画出“速度线”(运动轨迹在初始位置的切线)与“力线”(在初始位置电场线的切线方向),从二者的夹角情况来分析曲线运动的情景.
(2)“三不知时要假设”——电荷的正负、场强的方向(或等势面电势的高低)、电荷运动的方向,是题意中相互制约的三个方面.若已知其中的任一个,可顺次向下分析判定各待求量;若三个都不知(三不知),则要用“假设法”分别讨论各种情况.
考点三 静电力作用下的平衡问题 例题
1.解决这类问题与解决力学中的平衡问题的方法步骤相同,只不过是多了静电力而已.
2.(1)解决静电力作用下的平衡问题,首先应确定研究对象,如果有几个物体相互作用时,要依据题意,适当选取“整体法”或“隔离法”.
(2)电荷在匀强电场中所受电场力与位置无关;库仑力大小随距离变化而变化.
考点四 对称法 填补法 等效法 叠加电场的题
1.对称法:
利用空间上对称分布的电荷形成的电场具有对称性的特点,使复杂电场的叠加计算问题大为简化.
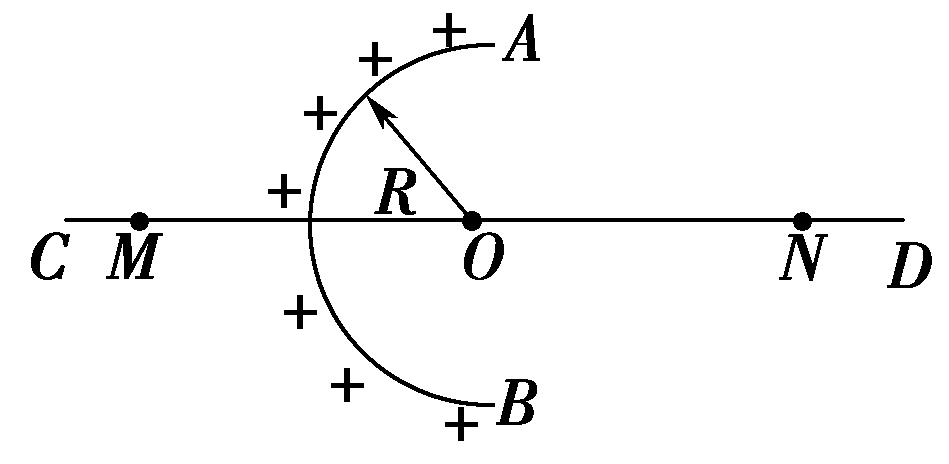
例如:如图所示,均匀带电的4球壳在O点产生的场强,等效为弧BC产生的场强,弧BC产生的场强方向,又等效为弧的中点M在O点产生的场强方向
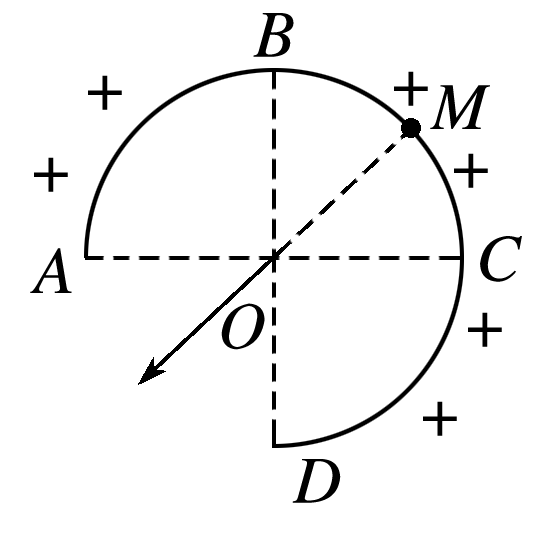
2.填补法 例题
将有缺口的带电圆环或圆板补全为完整的圆环或圆板,或将半球面补全为球面,从而化难为易、事半功倍.
若将带电量为2q的球面放在O处,均匀带电的球壳在球外空间产生的电场等效于电荷集中于球心处产生的电场.则在M点所产生的电场为$E_{2Q}=\frac{kq}{2R^2}$,而将右侧去掉只剩左侧,M处的场强为E,说明右侧去掉部分在M处产生的场强为E′=$\frac{kq}{2R^2}-E$,根据对称性,左侧没去掉部分在右侧N点产生的场强也为$\frac{kq}{2R^2}-E$
3.等效法
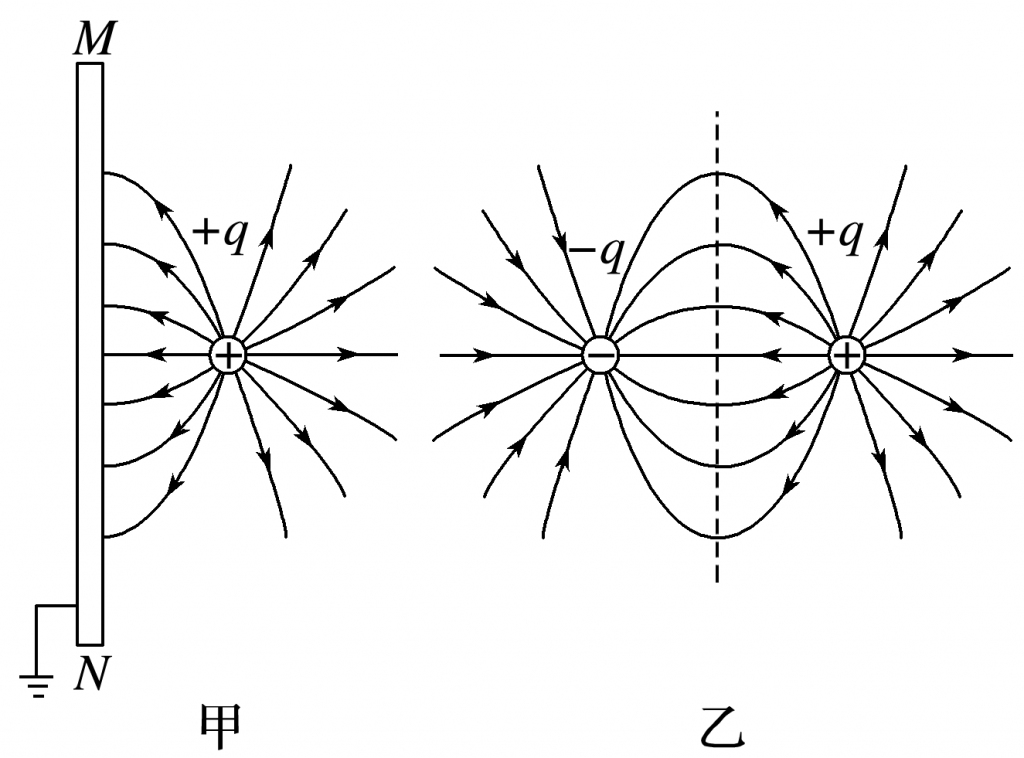
在保证效果相同的前提下,将复杂的电场情景变换为简单的或熟悉的电场情景.
例如:一个点电荷+q与一个无限大薄金属板形成的电场,等效为两个异种点电荷形成的电场,如图甲、乙所示.