电容器与电容模型例题
超级电容无轨电车行驶时无需拖着长辫连接电缆,只需在候客上车间隙连接供电网充电几十秒,就可保证行驶所需的电能,既环保,又美观.我国成功研制了世界最高水平的“3.0V,1200F”石墨烯超级电容器.超级电容器充电时,电极表面将吸引周围电解质溶液中的异性离子,使这些离子附着于电极表面上形成相距小于0.5mm、相互绝缘的等量异种电荷层,石墨烯电极结构使得该异种电荷层的面积成万倍增加.下面有关说法正确的是( )
A.该电容器充满电后的电量为36000C
B.该电容器最多能储存108000J的电能
C.超级电容器电容大的原因是其有效正对面积大、板间距离小
D.当该电容器放电至两端电压为1.5V时,其电容变为600F

展开答案
【答案】AC
【解析】根据“3.0V,1200F”,结合$C=\dfrac{Q}{U}$,$Q=CU=12000X3.0=36000$故A正确,计算的时候小心小数点,高中最要纠正的就是小数点的问题。用科学计数法会好很多,我示范的是不好的过程。
该电容器储存的电能为$W=UQ=CU^2$,如果这样推理就错了,因为电容的电压会随着电荷减少而减少,所以正确的做法应该平均化,也就是$W=UQ=\frac{1}{2}CU^2=\dfrac{1}{2}\times 1.2\times 10^4 \times 3.0^2=5.4\times10^4j$ 。B错误。
$C=\dfrac{\varepsilon S}{4\pi kd}$,根据决定式C对D不对。
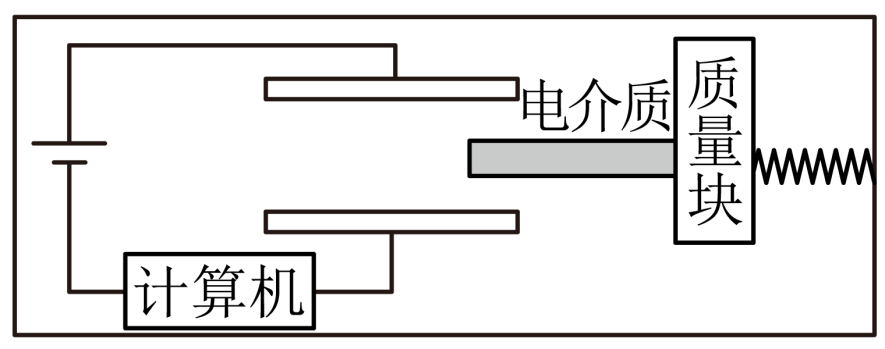
(2022·湖北·高二期末)(多选)我国国产东风洲际弹道核导弹可突破西方国家的防空反导系统,具有很强的战略威慑力,其内部固定安装有多种类型的传感器。例如电容式导弹加速度传感器原理如图所示,质量块左、右侧分别连接电介质和轻质弹簧,弹簧与电容器固定在武器身体内部,质量块套在光滑且平行于弹簧轴线的固定直杆上,质量块可带动电介质移动从而改变电容。则( )
A.电介质插入极板间越深,则电容器电容越大
B.导弹沿弹簧轴线方向向右做加速运动,则电路中一定有电流
C.导弹由静止突然沿弹簧轴线方向向右匀加速运动时,电路中有顺时针方向的电流
D.导弹沿弹簧轴线方向向右匀加速运动过程中突然开始匀速,稳定后弹簧长度会变长
展开答案
【答案】AC
【详解】A.根据电容器的电容公式$C=\dfrac{\xi S}{4\pi kd}$可知,当电介质插入极板间越深,即电介质增大,则电容器电容越大,选项A正确;
B.当传感器以恒定加速度运动时,根据牛顿第二定律可知,弹力大小不变,则电容器的电容不变,因两极的电压不变,则电容器的电量不变,因此电路中没有电流,选项B错误;
C.当传感器由静止突然向右加速瞬间,质量块要向左运动,导致插入极板间电介质加深,因此电容会增大,由于电压不变,根据Q=CU可知,极板间的电量增大,电容器处于充电状态,因此电路中有顺时针方向电流,选项C正确;
D.若传感器原来向右匀加速运动变为向右匀速运动,质量块受到向右的弹簧的弹力将变小,弹簧长度会变小,选项D错误。
故选AC。
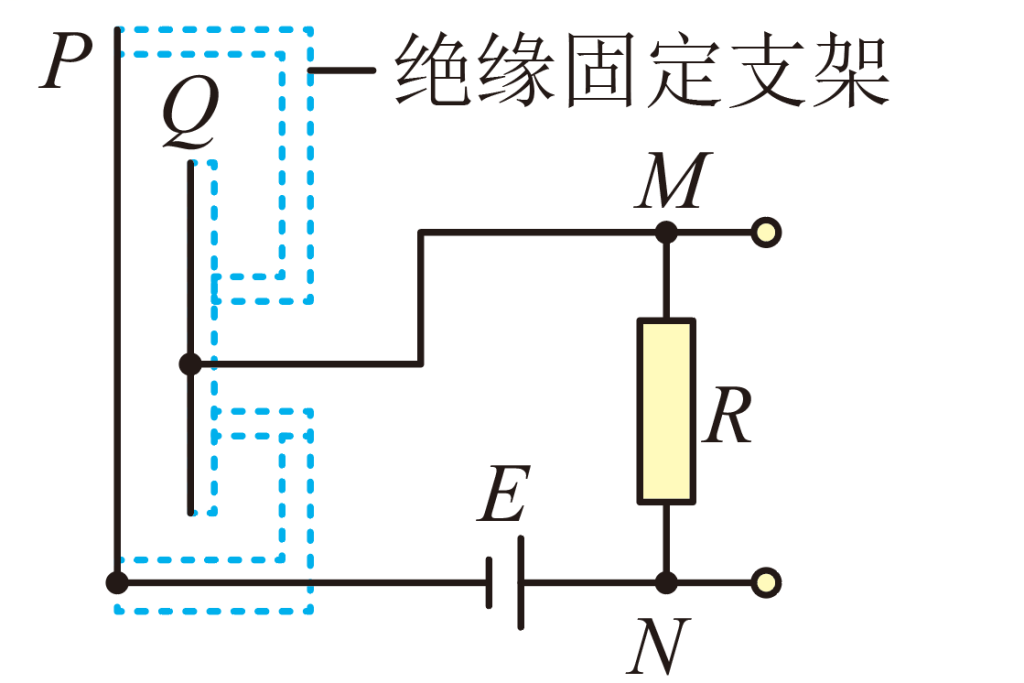
(2010·重庆·高考真题)某电容式话筒的原理示意图如图所示,E为电源,R为电阻,薄片P和Q为两金属基板,对着话筒说话时,P振动而Q可视为不动,在P、Q间距增大过程中,
A.P、Q构成的电容器的电容增大
B.P上电荷量保持不变
C.M点的电势比N点的低
D.M点的电势比N点的高
展开答案
【答案】D
【详解】电容式话筒与电源串联,电压保持不变,在P、Q间距增大过程中,根据电容决定式$C=\dfrac{\xi S}{4\pi kd}$得电容减小,又根据电容定义式$C=\dfrac{Q}{U}$得电容器所带电量减小,电容器的放电电流通过R的方向由M到N,所以M点的电势比N点的高,故ABC错,D正确。
故选D。
工厂在生产纺织品、纸张等绝缘材料时,为了实时监控其厚度,通常要在生产流水线上设置如图所示传感器。其中A、B为平行板电容器的上、下两个极板,上下位置均固定,且分别接在恒压直流电源的两极上(电源电压小于材料的击穿电压)。当流水线上通过的产品厚度减小时,下列说法正确的是( )
A.A、B平行板电容器的电容增大
B.A、B两板间的电场强度减小
C.A、B两板上的电荷量变大
D.有电流从a向b流过灵敏电流计
展开答案
【答案】D
【解析】电容器始终与恒压电源相连,其两极板间的电势差U不变,根据
$C=\dfrac{\varepsilon S}{4\pi kd}$
可知,当产品厚度减小,导致εr减小时,电容器的电容C减小,再根据Q=CU
可知极板带电荷量Q减小,有放电电流从a向b流过灵敏电流计,AC错误,D正确;
B.因两板之间的电势差不变,板间距不变,所以两板间的电场强度$E=\dfrac{U}{d}$不变,B错误。
几乎所有人都会愿意思考的会问,这个εr到底什么意思?一文读懂介电性能—介电常数
若它们射入如图所示,质子、氘核和氦核都沿平行板电容器两板中线OO′方向垂直于电场线射入板间的匀强电场,射出后都打在同一个与OO′垂直的荧光屏上,使荧光屏上出现亮点.下列说法中正确的是( )
A、若它们射入电场时的速度相等,在荧光屏上将出现3个亮点
B、若它们射入电场时的动量相等,在荧光屏上将只出现2个亮点
C、若它们射入电场时的动能相等,在荧光屏上将只出现1个亮点
D、若它们是由同一个电场从静止加速后射入此偏转电场的,在荧光屏上将只出现1个亮点
展开答案
【答案】D
【解析】:A、三种粒子带电量不同,分别为q、q、2q;质量不同,分别为m、2m、4m.很多同学第一反应尝试一一计算,其实不需要,我们列出一个通式观察一下即可。
$a=\dfrac{qE}{m}$
$y=\dfrac{1}{2}at^2$
$T=\dfrac{L}{v}$三个式子联立
$y=\dfrac{qEL^2}{2mv_0^2}$
若它们射入电场时的速度相等,y与比荷(电荷量与质量的比值)成正比,而三个粒子中质子的比荷最大,氘核和α粒子的比荷相等,在荧光屏上将出现2个亮点.故A错误.
B、若它们射入电场时的动量相等
$y=\dfrac{qEL^2}{2mv_0^2}=\dfrac{qmEL^2}{2m^2v_0^2}$
可见y与qm成正比,三个qm都不同,则在荧光屏上将只出现3个亮点.故B错误.
C、若它们射入电场时的动能相等,y与q成正比,在荧光屏上将只出现2个亮点.故C错误.
D、若它们是由同一个电场从静止加速后射入此偏转电场的,根据推论可知,y都相同,故荧光屏上将只出现1个亮点.
图(a)为示波管的原理图。如果在电极YY’之间所加的电压图按图(b)所示的规律变化,在电极XX’之间所加的电压按图(c)所示的规律变化,则在荧光屏上会看到的图形是()
展开答案
【答案】B
【解析】示波管的YY′偏转电压上加的是待显示的信号电压,XX′偏转电极通常接入锯齿形电压,即扫描电压,当信号电压与扫描电压周期相同时,就可以在荧光屏上得到待测信号在一个周期内的稳定图象.
在0~2t1时间内,扫描电压扫描一次,信号电压完成一个周期,当UY为正的最大值时,电子打在荧光屏上有正的最大位移,当UY为负的最大值时,电子打在荧光屏上有负的最大位移,UX 为负的最大值时在X负方向最大,然后向正方向移动。所以选B
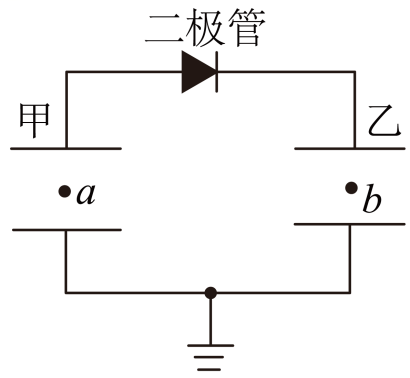
(2022·湖南·长郡中学模拟预测)如图所示,甲、乙为两个相同的平行板电容器,它们的极板均水平放置,上极板间连有一个二极管,下极板均接地。a、b是电荷量相同、质量分别为m1、m2的带负电油滴。当甲、乙的电荷量分别为Q1、Q2时,油滴a、b恰好分别悬浮在甲、乙的极板之间,则下列说法可能正确的是( )
A.Q1大于Q2
B.m1大于m2
C.将甲的上极板向上平移少许,a向下运动,b向上运动
D.将乙的上极板向右平移少许,a向下运动,b向上运动
展开答案
【答案】C
【解析】
在一柱形区域内有匀强电场,柱的横截面是以O为圆心,半径为R的圆,AB为圆的直径,如图所示。质量为m,电荷量为q(q>0)的带电粒子在纸面内自A点先后以不同的速度进入电场,速度方向与电场的方向垂直。已知刚进入电场时速度为零的粒子,自圆周上的C点以速率$v_0$穿出电场,AC与AB的夹角60°。运动中粒子仅受电场力作用。
(1)求电场强度的大小;
(2)为使粒子穿过电场后的动能增量最大,该粒子进入电场时的速度应为多大?
(3)为使粒子穿过电场前后动量变化量的大小为$mv_0$,该粒子进入电场时的速度应为多大?
展开答案
【解析】
这类题的难点在于如何解读,而不在公式的记忆,重点的话在于:“电粒子在纸面内自A点先后以不同的速度进入电场,速度方向与电场的方向垂直。”
也就是说速度始终和电场垂直,速度是变化的。
那么当速度为0,就是匀加速运动,不为0就是抛物运动。
(1) 粒子初速度为零,由动能定理可知力做功都变成了动能,角∠BAC=60°,所以AC=R
$F\times AC = \dfrac{1}{2}mv_0^2$
$F=Eq$
$E=\dfrac{mv_0^2}{2qR}$
(2)动能增加量最大,我们都知道肯定是力做功最多的那个位移。转换一下就是离开A点电势最高的地方。
顺着这个思路,我们可以轻易得出电场线的方向,那么D点和A点的电势差最大,自然也就不难判断各自的角度关系。$DP=\dfrac{\sqrt{3}}{2}R$,$AP=\dfrac{3}{2}R$,计算的时候先准备好基础数据,并且确认后,再继续,用制度解决粗心带来的错误。
$Eq=ma$
$AP=\dfrac{3}{2}R=\dfrac{1}{2}at^2$
$DP=\dfrac{\sqrt{3}}{2}R=v_1t$
$v_1=\dfrac{\sqrt{2}}{4}v_0$
按理标准解题结束,但是我发现80%的人是不能计算出结果的,其根本原因就是混乱,没有条理,计算前,要先观察,以下是示范过程,草稿纸也尽量如此。
(2)动量变化一样,说明在力的方向作用时间一样,必然从B点出去。
$2Rsin60 ^\circ = v_2t$
$R = \dfrac{1}{2}at^2$
$a=\dfrac{v_0^2}{2R}$
解得:$v_2=\dfrac{\sqrt{3}}{2}v_0$
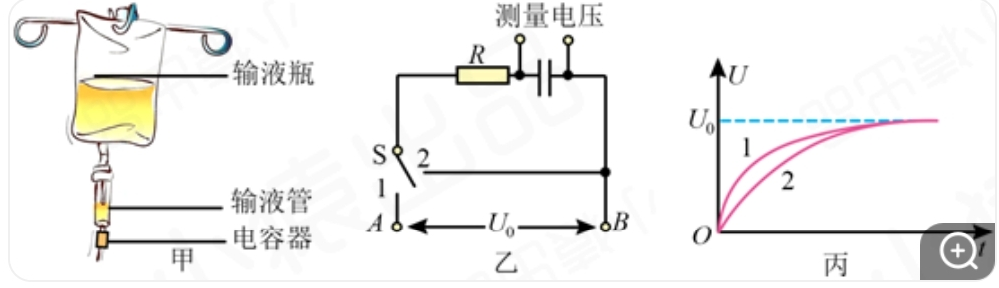
目前大多数医院进行输液治疗时都采用传统的人工监护方式,为减轻医务人员负担,有不少输液传感器投入使用。某电容输液传感器测量装置示意图如图甲所示,测量电路如图乙所示,A、B间接入恒定电压Uo,自动控制开关S置于1时电容器充电、置于2时电容器放电。电容器在S的作用下周期性充放电,系统监测每次充电过程中电容器两端电压随时间的变化曲线,可自动判定输液管中是否有药液。在输液管中有药液和无药液的两次电容器充电过程中,电容器两端电压随时间的变化曲线如图丙所示,已知有药液时测量电路中的电容值更大,则( )
A.曲线1为有药液时的充电曲线
B.曲线2为有药液时的充电曲线
C.曲线1对应的情况下电容器充满电后所带的电荷量较大
D.曲线2对应的情况下电容器充满电后所带的电荷量较大
展开答案
【答案】BD
【分析】因为电容增加,所以充满电,电荷量就要增加,根据图像可以看到充电时间一样,所以只需要分析电流大小即可!
$I=\dfrac{U_0-U}{R}$
很明显1的平均电压高,所以电流小,相同时间电荷就少,所以选B D
多反射飞行时间质谱仪是一种测量离子质量的新型实验仪器,其基本原理如图所示,从离子源A处飘出的离子初速度不计,经电压为U的匀强电场加速后射入质量分析器。质量分析器由两个反射区和长为l的漂移管(无场区域)构成,开始时反射区1、2均未加电场,当离子第一次进入漂移管时,两反射区开始加上电场强度大小相等、方向相反的匀强电场,其电场强度足够大,使得进入反射区的离子能够反射回漂移管。离子在质量分析器中经多次往复即将进入反射区2时,撤去反射区的电场,离子打在荧光屏B上被探测到,可测得离子从A到B的总飞行时间。设实验所用离子的电荷量均为q,不计离子重力。
(1)求质量为m的离子第一次通过漂移管所用的时间T1;
(2)反射区加上电场,电场强度大小为E,求离子能进入反射区的最大距离x;
(3)已知质量为m0的离子总飞行时间为t0,待测离子的总飞行时间为t1,两种离子在质量分析器中反射相同次数,求待测离子质量m1。
展开答案
【分析】(1)设离子经加速电场加速后的速度大小为v,有
$Uq=\dfrac{1}{2}mv^2$①
$T_1=\dfrac{l}{v}$
解得:$T_1=\sqrt{\dfrac{ml^2}{2qU}}$
(2)根据动能定理,有
$qU-qEx=0$(很多学生喜欢直接写等式,建议大家用方程,可以深刻的理解能量变化带来的效果)
$X=\dfrac{U}{E}$
(3)离子在加速电场中运动和反射区电场中每次单向运动均为匀变速直线运动,平均速度大小均相等,设其为$\overline{v}$,有
$\overline{v}=\dfrac{v}{2}$ ⑥
离子在反射区的电场中运动路程是与离子本身无关的,所以不同离子在电场区运动的总路程相等,设为$L_1$,在无场区的总路程设为$L_2$,根据题目条件可知,离子在无场区速度大小恒为v,设离子的总飞行时间为t总。有
t总 = $\dfrac{L_1}{\overline{v}}+\dfrac{L_2}{v}$⑦
联立①⑥⑦式,得
t总 = $(2L_1+L_2)\sqrt{\dfrac{m}{2qU}}$
可见,离子从A到B的总飞行时间与$\sqrt{m}$成正比。由题意可得
$\dfrac{t_1}{t_0}=\sqrt{\dfrac{m_1}{m_0}}$
可得$m_1=(\dfrac{t_1}{t_0})^2m_0$
