电容器与电容

---

2．电容

(1)定义是：$C=\frac{Q}{U}$

(2) 单位：法拉（F）1F=10⁶uF =10¹²pF

3．平行板电容器

(1)影响因素：平行板电容器的电容与正对面积成正比，与介质的介电常数成正比，与两极板间距离成反比．

决定式：$C=\frac{\xi S }{4\pi Kd}$

特别提醒：$C=\frac{Q}{U}$适用于任何电容器，但是$C=\frac{\xi S }{4\pi Kd}$仅适用于平行板电容。

二、带电粒子在电场中的运动

1．加速问题

(1)匀强电场：$W=qED=qU=\frac{1}{2}mv^2-\frac{1}{2}m{v_0}^2$

(2)在非匀强电场中：$W=qU=\frac{1}{2}mv^2-\frac{1}{2}m{v_0}^2$

2．偏转问题

(1)条件分析：不计重力的带电粒子以速度v₀垂直于电场线方向飞入匀强电场．

(2)运动性质：匀变速曲线运动．

(3)处理方法：利用运动的合成与分解．

①沿初速度方向：做匀速运动．

②沿电场方向：做初速度为零的匀加速运动．

特别提示：带电粒子在电场中的重力问题

(1)基本粒子：如电子、质子、α粒子、离子等除有说明或有明确的暗示以外，一般都不考虑重力(但并不忽略质量)．

(2)带电颗粒：如液滴、油滴、尘埃、小球等，除有说明或有明确的暗示以外，一般都不能忽略重力．

---

考点一　平行板电容器的动态分析

---

运用电容的定义式和决定式分析电容器相关量变化的思路

1．确定不变量，分析是电压不变还是所带电荷量不变．

(1)保持两极板与电源相连，则电容器两极板间电压不变．

(2)充电后断开电源，则电容器所带的电荷量不变．

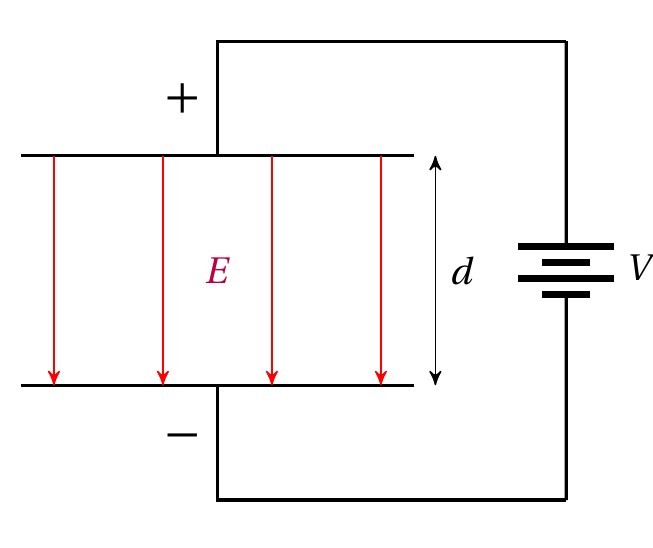
\begin{cor} 通过以下三个公式的组合可以判断场强变化，从而确定力的大小。

\begin{itemize}\item 电容决定式：$C=\frac{\xi S }{4\pi Kd}$ 计算式：$C=\frac{Q}{U}$ 场强计算式：$E=\frac{U}{d}$ \end{itemize}\end{itemize}

\end{itemize} \end{cor}

5.在分析平行板电容器的动态变化问题时，必须抓住两个关键点：

(1)确定不变量：首先要明确动态变化过程中的哪些量不变，一般情况下是保持电量不变或板间电压不变．

(2)恰当选择公式：要灵活选取电容的两个公式分析电容的变化，还要应用E＝d(U)，分析板间电场强度的变化情况．

考点二　带电粒子在电场中的直线运动

---

1．运动类型

(1)带电粒子在匀强电场中做匀变速直线运动．

(2)带电粒子在不同的匀强电场或交变电场中做匀加速、匀减速的往返运动．

2．分析思路

(1)根据带电粒子受到的电场力，用牛顿第二定律求出加速度，结合运动学公式确定带电粒子的运动情况．

(2)根据电场力对带电粒子所做的功等于带电粒子动能的变化求解．此方法既适用于匀强电场，也适用于非匀强电场．

(3)对带电粒子的往返运动，可采取分段处理．

考点三　带电粒子在电场中的偏转　

---

基本规律

(1)沿初速度方向做匀速直线运动，运动时间$t=\dfrac{l}{v_0}$；
(2)沿电场力方向做初速度为零的匀加速直线运动，加速度$a=\dfrac{F}{m}=\dfrac{qE}{m}=\dfrac{qU}{m}$；
(3)离开电场时的偏移量$y=\dfrac{1}{2}at^2=\dfrac{qUt^2}{2mdv_0^2}$；
(4)离开电场时的偏转角$\varphi$满足$tan \varphi = \dfrac{v_y}{v_0} = \dfrac{at}{v_0} = \dfrac{qUt}{mdv_0^2}$.
解决此类问题的关键时利用正交分解的思想来处理类平抛运动。常见的思路由两种：一种时正交分解位移，另一种时正交分解速度。

---

带电粒子在交变电场中的偏转

---

1．注重全面分析(分析受力特点和运动特点)，找到满足题目要求所需要的条件．

2．比较通过电场的时间t与交变电场的周期T的关系：

(1)若t≪T，可认为粒子通过电场的时间内电场强度不变，等于刚进入电场时刻的场强．

(2)若不满足上述关系，应注意分析粒子在电场方向上运动的周期性．

对称思想、等效思想在电场问题中的应用

---

一、割补法求解电场强度

由于带电体不规则，直接求解产生的电场强度较困难，若采取割或补的方法，使之具有某种对称性，从而使问题得到简化．

二、等效法求解电场中的圆周运动

1.带电粒子在匀强电场和重力场组成的复合场中做圆周运动的问题是一类重要而典型的题型．对于这类问题，若采用常规方法求解，过程复杂，运算量大．若采用“等效法”求解，则过程往往比较简捷．

2.等效法求解电场中圆周运动问题的解题思路：

(1)求出重力与电场力的合力F合，将这个合力视为一个“等效重力”．

(2)将a＝m(F合)视为“等效重力加速度”．

(3)将物体在重力场中做圆周运动的规律迁移到等效重力场中分析求解．