电势和电势能模型例题
如图所示,虚线是某电场线的等势线。一带电粒子只在静电力作用下恰能沿实线从A点运动到C点,则()
A.粒子一定带负电
B.粒子在A点的电势能大于C点的电势能
C.A点的电场强度大于C点的电场强度
D.粒子从A点到B点静电力所做功大于B点到C点静电力所做的功。
展开答案
【答案】C
【解析】 电场线与等势面垂直,且电场线由电势高指向电势低的方向。所以图中电场线方向应该向左,因为带电粒子由A运动到C,且方向逐渐向曲线内侧靠拢,所以粒子运动方向和电场线方向一致,所以带正电。故A错误。
A点电势能小于C,所以B错。由于AB,BC电势差一样,所以电场力做功也一样。等势线密集的地方电场强度大,故C正确。
匀强电场中的点A、B、C、D、E、F、G、H,为立方体的八个顶点。已知GFBD点的电势分别为5、1、2、4v,则A点的电势为()
A.0V B.1V C.2V D.3V
展开答案
【解析】
当在匀强电场中沿电场线方向距离相等时,电势差必定相等,因为GF//CB,GF=CB,所以$\varphi_G-\varphi_F=\varphi_C-\varphi_B$
解得:$\varphi_C=\varphi_G-\varphi_F+\varphi_B=5v-1v+2=6v$
同理可知 $\varphi_A-\varphi_B=\varphi_D-\varphi_C$
解得:$\varphi_A-\varphi_B=\varphi_D-\varphi_C=2v+4v-6v=0$
方法二如右图
静电场的方向平行于x轴,沿x轴上各点的场强与位置关系如图所示。一质子仅受电场力,由O点静止释放,沿x轴正方向运动,已知$Oa=ab=bc=L$,$\varphi _b =0$
A.a点的电势为$E_0L$
B.质子在O点和d点的电势能相等
C.质子在abc三点的动能之比为1:2:3
D.质子从O点到b点先做匀加速直线运动后做匀减速直线运动
展开答案
【答案】AC
【解析】质子一直加速运动,动能一直增加,增加的动能就是减少的电势能,因为b的电势为0,图像围成的面积就是电势差,故$\varphi_0=U_{ab}=E_0L$.故A正确,B错误。因为Oa=ab=bc,围成的面积相同,电势差也相同,那么每次做功增加量都一样,根据 W=UQ所以动能1:2:3 ;质子只受到电场力的作用,$F=Eq=ma$,因为电场是变化的,所以加速度不是定值,D错误。
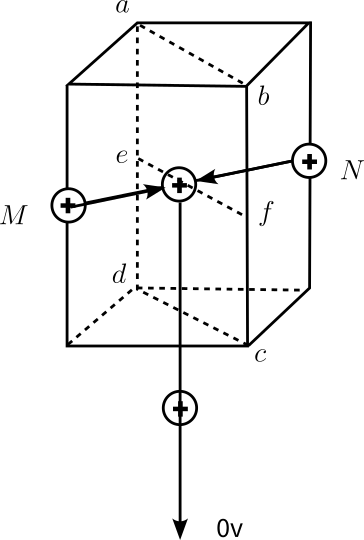
如图所示的水平匀强电场中,将两个带电小球M和N分别沿图示路径移动到同一水平线上的不同位置,释放后,MN保持静止,不计重力,则()
A.M的带电量比N大
B.M带负电荷,N带正电荷
C.静止时M受到的合力比N大
D.移动过程中匀强电场对M做负功
展开答案
【答案】D
【解析】
由释放后移动到M、N均保持静止知所受合力为零,M和N受到的电场力同M、N之间的库仑力平衡,二者大小相等、方向相反,分析可知M带负电荷,N带正电荷,且M、N带电量相等,故A、B错误;静止时M、N受到的合力均为零,故C错误;因N带正电,所受电场力方向向右,与位移方向夹角为钝角,所以做正功。故选D。
一均匀带电的绝缘球球心位于坐标原点O,规定x轴的正方向为电场正方向,则沿x轴的电场强度如图所示,下列说法正确的是
A.球体半径大小为$x_0$
B.$x>x_0$时,电场方向沿x轴负方向
C.$x=x_2$位置比$x=x_1$位置电势低
D.$x=-x_0$位置与$x=x_0$位置电势相等
展开答案
【答案】AD
【解析】
设绝缘球半径为$R$,总的电荷量为$Q$,则绝缘球内部电场的强度
$$E=k\dfrac{q}{x^2}=\dfrac{Q\dfrac{{x}^3}{R^3}}{x^2}=k\dfrac{xQ}{R^3}$$
$E$与$x$成正比,故A正确。
根据题意,知球是带正电,电场方向在在x正轴一直为正,在x负轴方向一直为负。 B错误。
沿电场线方向电势降低,结合对称性,$x_2$比$x_1$电势高。
根据点电荷的电场线分布知$x=-x_0$位置与$x=x_0$位置电势相等,故D正确。
【扩展训练】
四个带电粒子的电荷量和质量分别为(+q,m)、(+q,2m)、(+3q,3m)、(−q,m),它们先后以相同的速度从坐标原点沿 x 轴正方向射入一匀强电场中,电场方向与 y 轴平行。不计重力,下列描绘这四个粒子运动轨迹的图像中,可能正确的是( )
展开答案
【解析】 带电粒子垂直进入匀强电场做类平抛运动,设水平位移为x,垂直位移为y,初速度为v0 ,则轨迹方程为
$y=\dfrac{1}{2}\times \dfrac{Eq}{m}(\dfrac{x}{v_0})^2=\dfrac{Eqx^2}{2mv_0^2}$
由于粒子的初速度相同,粒子的轨迹取决于$\dfrac{q}{m}$和电性。电荷个质量比值一样的(+q,m)、(+3q,3m)轨迹重合,且(+q,m)、(-q,m)、轨迹与x轴对称,(+q,m)比(+q,2m)弯曲度大,故选AD。
半径为R1和R2(R2>R1)的两无限长竖直同轴圆柱面,单位长度上分别带有等量异种电荷如题图1所示,内圆柱面带正电。已知电场强度沿某一水平半径的分布情况如图2所示,当r<R1及r>R2时电场强度均为零,A、B分别为靠近内外圆柱面且同一半径上的两点,则( )
A.内圆柱面内各点电势可能不等
B.负试探电荷在A点时的电势能比在B点时的电势能大
C.A、B中点处的电场强度大于$\dfrac{E_A+E_B}{2}$
D.A、B两点的电势差小于$\dfrac{(E_A+E_B)(R_2-R_1)}{2}$
展开答案
【答案】D
【解析】A.内圆柱面和外圆柱面都是等势面,柱面上各点电势都相等,选项A错误;
B.电场线由A指向B,则A点电势高,则负试探电荷在A点时的电势能比在B点时的电势能小,选项B错误;
C.由图像可知,A、B中点处的电场强度小于$\dfrac{E_A+E_B}{2}$,选项C错误;
D.根据U=Ed,可知E-r图像与坐标轴围成的面积等于电势差,若从A到B的E–r图像为直线,则A、B两点的电势差等于$\dfrac{(E_A+E_B)(R_2-R_1)}{2}$
而此时图像的面积小于可知,A、B两点的电势差小于$\dfrac{(E_A+E_B)(R_2-R_1)}{2}$,选项D正确。
如图所示,在竖直平面内有水平向左的匀强电场,在匀强电场中有一根长为L的绝缘细线,细线一端固定在O点,另一端系一质量为m的带电小球。小球静止时细线与竖直方向成θ角,此时让小球获得初速度且恰能绕O点在竖直平面内沿逆时针方向做圆周运动,重力加速度为g。下列说法正确的是( )
A.匀强电场的电场强度 $E=\dfrac{mg tan\theta}{ q}$
B.小球动能的最小值为$E_k=\dfrac{mgL}{ 2cos \theta}$
C.小球运动至圆周轨迹的最高点时机械能最小
D.小球从初始位置开始,在竖直平面内运动一周的过程中,其电势能先减小后增大
展开答案
【答案】AB
【解析】A.小球静止时悬线与竖直方向成θ角,对小球受力分析,小球受重力、拉力和电场力,三力平衡,根据平衡条件,有$mg tan \theta =qE$
解得$E=\dfrac{mg tan\theta}{ q}$ 选项A正确;
B.小球恰能绕O点在竖直平面内做圆周运动,在等效最高点A速度最小,根据牛顿第二定律,有$\dfrac{mg}{cos \theta}=m \dfrac{v^2}{L}$
则最小动能$E_k=\dfrac{1}{2}mv^2=\dfrac{mgL}{ 2cos \theta}$ 选项B正确;
C.小球的机械能和电势能之和守恒,则小球运动至电势能最大的位置机械能最小,小球带负电,则小球运动到圆周轨迹的最左端点时机械能最小,选项C错误;
D.小球从初始位置开始,在竖直平面内运动一周的过程中,电场力先做正功,后做负功,再做正功,则其电势能先减小后增大,再减小,选项D错误。
离子推进器已经全面应用于我国航天器,其工作原理如图所示,推进剂氙原子$P$喷注入腔室$C$后,被电子枪$G$ 射出的电子碰撞而电离,成为带正电的氙离子。氙离子从腔室$C$中飘移过栅电极$A$的速度大小可忽略不计,在栅电极$A$、$B$之间的电场中加速,并从栅电极 $B$ 喷出。在加速氙离子的过程中飞船获得反推力。已知栅电极A、B之间的电压为U,氙离子的质量为 m、电荷量为 q,AB 间距为 d,推进器单位时间内喷射的氙离子数目 n。则喷射离子过程中,对推进器产生的反冲作用力大小为( )
A.$n\sqrt{\dfrac{2qU}{m}}$ B.$nm\sqrt{2qU}$ C.$n\sqrt{2mqU}$ D.$n\sqrt{\dfrac{2m}{qU}}$
展开答案
【答案】C
【解析】 氙离子在栅电极A、B间经历直线加速过程,根据动能定理有
$qU=\dfrac{1}{2}mv^2$
解得 $\sqrt{\dfrac{2qU}{m}}$
由动量定理得 $$ F\Delta t=n \Delta t mv$$
解$n\sqrt{\dfrac{2m}{qU}}$
本题意在训练感觉,以后做题看到这这种就要知道时间和质量的关系。
如图所示,在竖直平面内xOy坐标系中分布着与水平方向成45°角的匀强电场,将一质量为m、带电荷量为q的小球,以某一初速度从O点竖直向上抛出,它的轨迹恰好满足抛物线方程x=ky2,且小球通过点P,已知重力加速度为g,则( )
A.电场强度的大小$\dfrac{mg}{q}$
B.小球初速度的大小为$\sqrt {\dfrac{g}{2k}}$
C.小球通过点P时的动能为$\dfrac{5mg}{4k}$
D.小球从O点运动到P点的过程中,电势能减少$\dfrac{\sqrt{2}mg}{k}$
展开答案
【答案】BC
【解析】A.小球做类平抛运动,则电场力与重力的合力沿x轴正方向,可知qE=mg$qE=mg$
电场强度的大小为$E= \dfrac{\sqrt{2}mg}{q}$故A错误;
B.因为F合=mg=ma
所以a=g
由类平抛运动规律有
$ \dfrac{1}{K}=v_0t, \dfrac{1}{K}= \dfrac{1}{2}gt^2$
得小球初速度大小为$v_0\sqrt{\dfrac{g}{2k}}$故B正确;
C.由P点的坐标分析可知$\dfrac{v_0}{v_x}=\dfrac{1}{2}$
所以小球通过点P时的动能为
$\dfrac{1}{2}mv^2=\dfrac{1}{2}m(v_0^2+v_x^2)=\dfrac{5mg}{4k}$故C正确;
D.小球从O到P过程中电势能减少,且减少的电势能等于电场力做的功,即
$W=qE\dfrac{1}{K}\dfrac{1}{cos 45^\circ}=\dfrac{2mg}{k}$故D错误。
绝缘粗糙的水平面上相距为6L的A、B两处分别固定电荷量不等的正电荷,两电荷的位置坐标如图甲所示,已知A处电荷的电荷量为+Q,图甲是A、B连线之间的电势φ与位置x之间的关系图像,图中x=L处对应图线的最低点,x=-2L处的纵坐标φ=2φ0,x=2L处的纵坐标φ=$\frac{6}{7}$φ0,若在x=-2L处的C点由静止释放一个质量为m、电荷量为+q的带电物块(可视为质点),物块随即向右运动(假设此带电物块不影响原电场分布),求:
(1)固定在B处的电荷的电荷量QB;
(2)小物块与水平面间的动摩擦因数μ为多大,才能使小物块恰好到达x=2L处?
(3)若小物块与水平面间的动摩擦因数$u=\dfrac{kQq}{12mgL^2}$,小物块运动到何处时速度最大?
展开答案
【解析】(1)由题图乙得x=L处为图线的最低点,切线斜率为零,即合场强为0,则有
$k\dfrac{Q_A}{r_A^2}=k\dfrac{Q_B}{r_B^2}$
代入数据得$Q_B=\dfrac{Q_A}{4}=\dfrac{Q}{4}$
(2)从x=-2L到x=2L的过程中,物块先做加速运动再做减速运动,由动能定理得,能量守恒经常用于处理运动问题。
$qU_1=\mu mgs_1$
即
$q(2\varphi_0 -\dfrac{6}{7}\varphi_0)=\mu mg(4L)$
解得
$\mu = \dfrac{2q\varphi_0}{7mgL}$
(3)小物块运动速度最大时,电场力与摩擦力的合力为零,设该位置离A点的距离为LA,则有
$k\dfrac{Q_Aq}{L_A^2}-k\dfrac{Q_Bq}{(6L-L_A)^2}=\mu mg$
带入数据简化
$\dfrac{4}{9L_A^2}-\dfrac{1}{(5L-L_A)^2}=\dfrac{1}{12L^2}$
此步骤鲜有人解出,作为高三学生最需要的就是训练计算能力,因为大多数人都会望而却步,物理层面一般考的不是纯计算能力,该猜就猜,LA肯定是整数,而且小于6,差值是12分之1,那么先试一下3L,验证正确,所以答案是,你在试卷上写:
解得$L_A=3L$
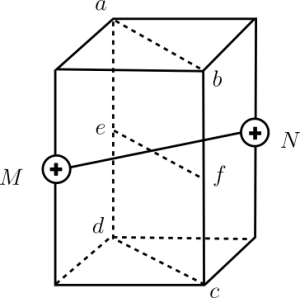
如图所示,两个等量正点电荷固定于M、N两点,边长与MN之间距离相等的正方形abcd位于与M、N连线垂直的平面上,e、f分别是ad、bc的中点,O怡好是MN和ef的中点。已知点电荷电场中某点$\varphi$($\varphi=k\dfrac{Q}{r}$导),Q为点电荷的电荷量,r为电场中某点到点电荷的距离,k为静电力常量。下列说法正确的是( )
A.b、d两点电场强度相同
B.沿正方形abcd四边移动电荷,电场力不做功
C.O点与e点的电势差等于e点与a点的电势差
D.将试探电荷+q由a点沿直线ac移动到c点,其电势能先增大后减小
展开答案
【答案】D
【解析】要重新理解什么是势能。
势能的定义:在力的方向上,因为位置不同而具有的能。
衡量势能的大小:在某位置开始运动,直到不能在运动了,这个过程所做的功就是势能。