运动的图像问题
图像问题三种思维方式:
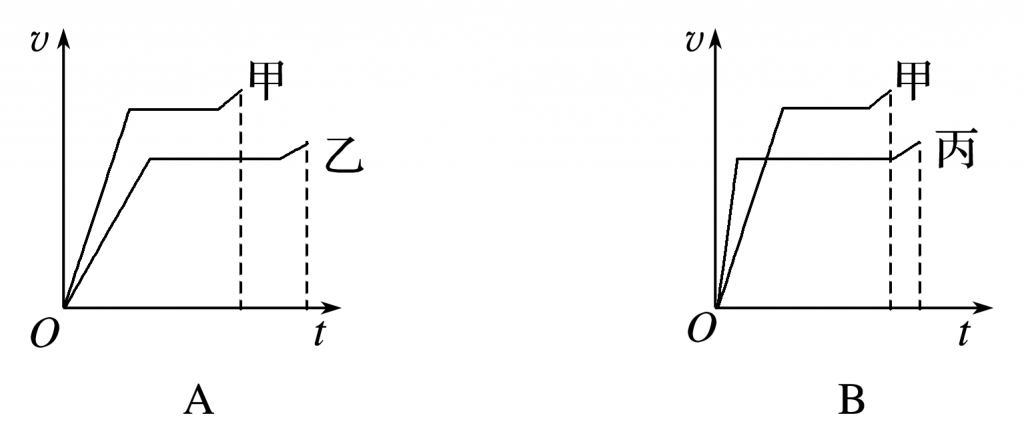
(多选)(2021·广东卷·8)赛龙舟是端午节的传统活动.下列v-t和s-t图像描述了五条相同的龙舟从同一起点线同时出发、沿长直河道划向同一终点线的运动全过程,其中能反映龙舟甲与其他龙舟在途中出现船头并齐的有
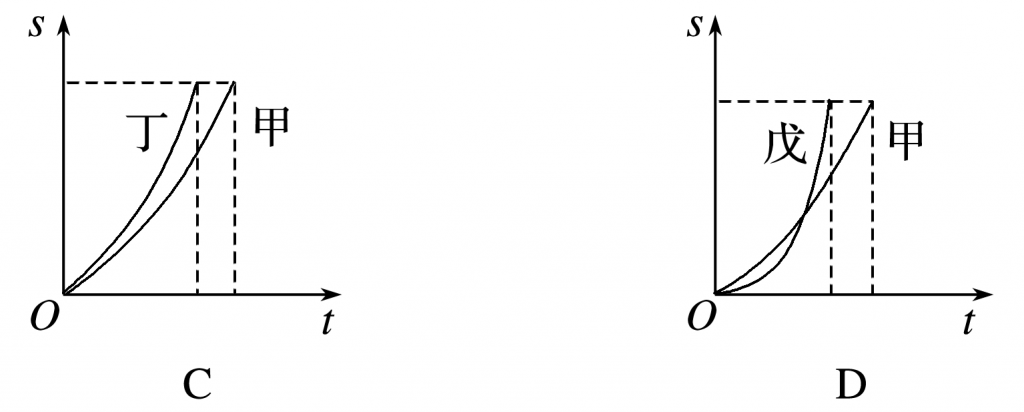
展开答案
【答案】 BD
【解析】 A图是v-t图像,由图可知,甲的速度一直大于乙的速度,所以中途不可能出现甲、乙船头并齐,故A错误;
B图是v-t图像,由图可知,开始丙的速度大,后来甲的速度大,v-t图像中图线与横轴围成的面积表示位移,由图可以判断在中途甲、丙位移会相同,所以在中途甲、丙船头会并齐,故B正确;
C图是s-t图像,由图可知,丁一直运动在甲的前面,所以中途不可能出现甲、丁船头并齐,故C错误;
D图是s-t图像,交点表示相遇,所以甲、戊在中途船头会并齐,故D正确.
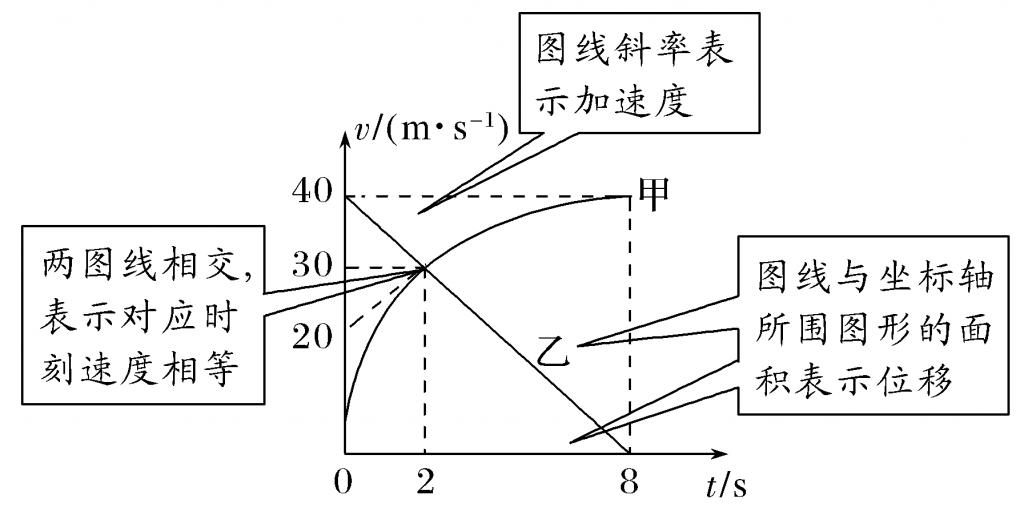
甲、乙两车在平直的公路上行驶,t=0时刻两车处于同一位置,其速度—时间图象如图所示,两图线交点处坐标及切线如图,则( )
A.t=8 s末,甲、乙两车相遇
B.t=2 s末,甲车的加速度大于乙车的加速度
C.在0~2 s内,甲车的位移小于乙车的位移
D.在2~8 s内,甲车的平均速度小于乙车的平均速度
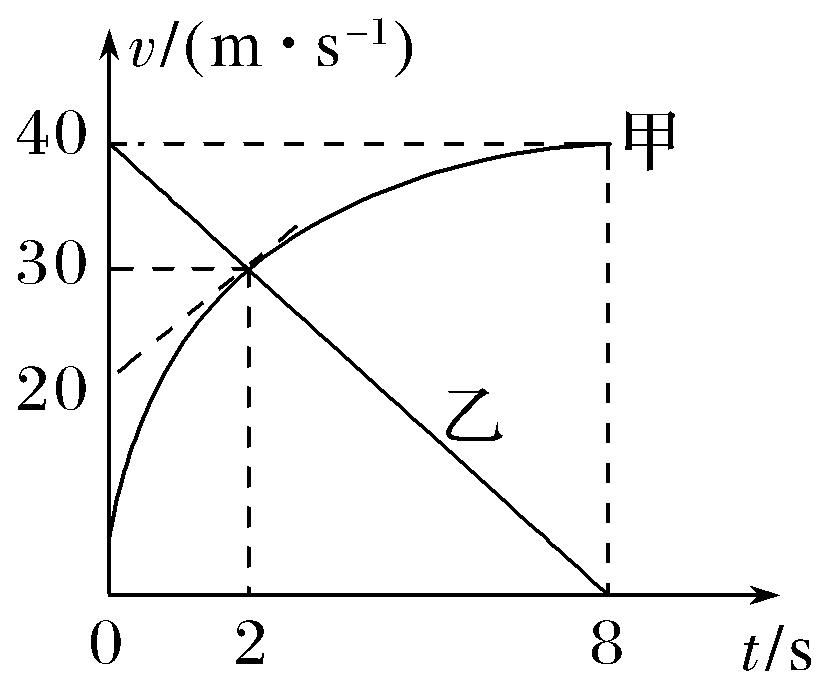
展开答案
【答案】 C
【解析】 根据速度—时间图线与坐标轴所围图形的面积表示位移可知,在0~8 s时间内,甲车的位移大于乙车的位移,又两车的初始位置相同,故t=8 s末,甲车在乙车前面,选项A错误;根据速度—时间图线的斜率表示加速度可知,在t=2 s时,甲车的加速度大小a1=5 m/s2,乙车的加速度大小a2=5 m/s2,甲、乙两车加速度大小相等,选项B错误;根据速度—时间图线与坐标轴所围图形的面积表示位移可知,在0~2 s时间内,甲车的位移小于乙车的位移,选项C正确;在2~8 s时间内,甲车的位移大于乙车的位移,根据平均速度公式可知,甲车的平均速度大于乙车的平均速度,选项D错误。
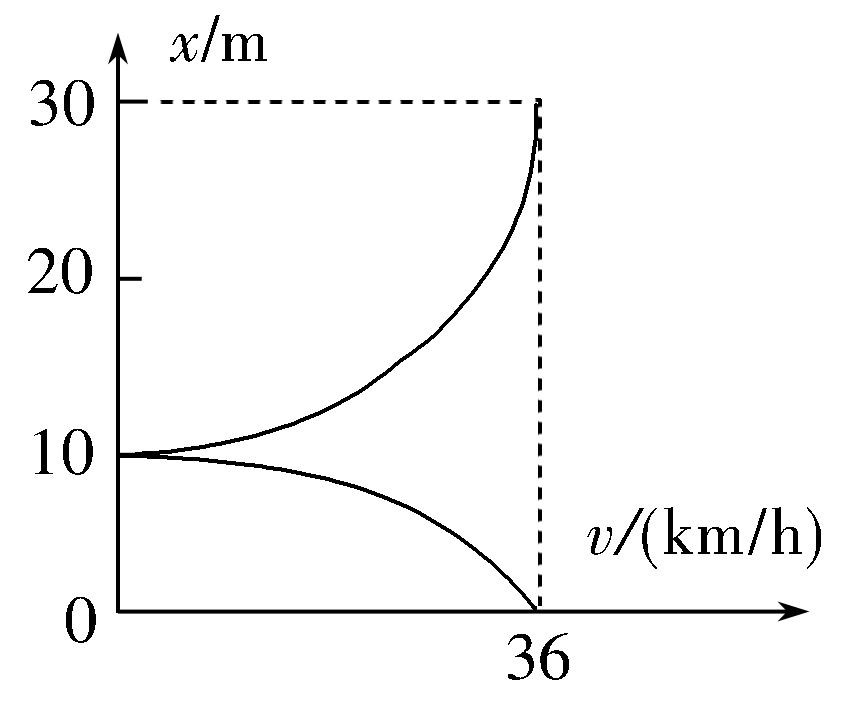
(2021年保定二模)为检测汽车的基本性能,某志愿者驾驶汽车以36 km/h的速度驶入水平长直试验场,某时刻开始刹车,汽车做匀减速直线运动直到速度减为0,然后马上使汽车做匀加速直线运动直到恢复最初的速度.从开始刹车到恢复最初速度的过程中汽车位移x与速度v的关系如图所示.下列说法中正确的是( )
A.汽车刹车过程中加速度的大小为5 m/s2
B.汽车加速过程中加速度的大小为10 m/s2
C.该过程中汽车的总位移为20 m
D.该过程所用总时间为4 s
展开答案
【答案】 A
【解析】 v0=36 km/h=10 m/s,
减速位移x1=10 m,
v02=2a1x1 a1=5 m/s2,t1=$\dfrac{v_0}{a_1}$=2 s,
加速过程
x2=(30-10) m=20 m,v02=2a2x2,a2=2.5 m/s2,
t2=$\dfrac{v_0}{a_2}$=4 s,则t=t1+t2=6 s.
(2021年唐山三模)(多选)一质点在0~6 s内竖直向上运动,其加速度a随时间t变化的关系图象如图所示,取竖直向下为加速度的正方向,重力加速度为g=10 m/s2,则下列说法正确的是( )
A.在0~2 s内质点发生的位移为20 m
B.在2~4 s内质点做加速运动
C.质点的初速度不小于66 m/s
D.在2~4 s内质点速度变化量为22 m/s
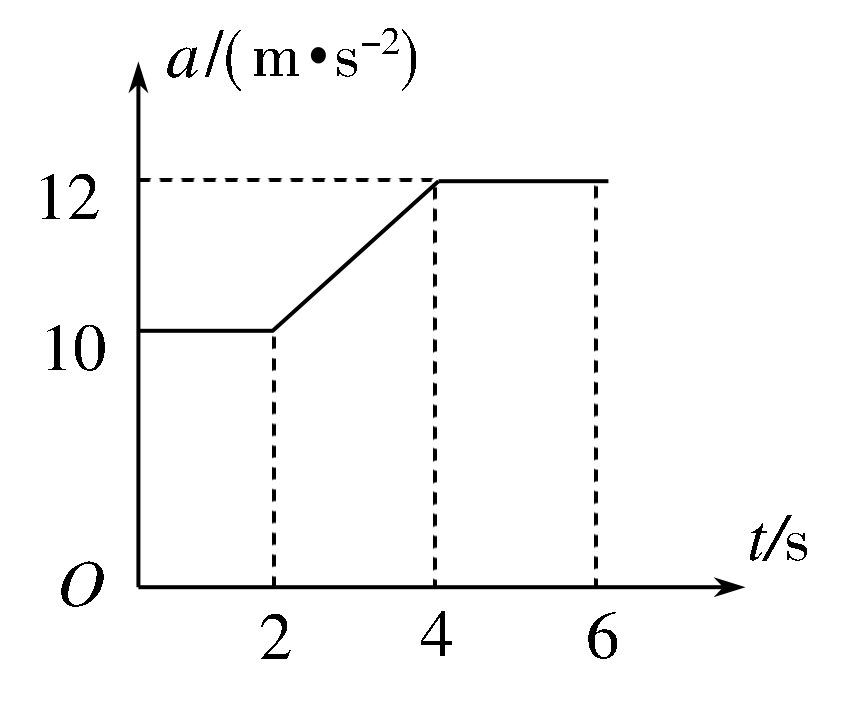
展开答案
【答案】:CD
【解析】:A.0~6s内物体向上运动初速度未知,不能求0~2s内位移,A错误;B.2~4s内速度与加速度反向,做加速度增大的减速运动,B错误;C.0~6s内速度变化量为a→t图象面积,故$\Delta v==2×10+\dfrac{10+12}{2}\times 2+12\times 2=66 $m/s,故初速度不小于66 m/s,C正确;D.2~4s内,$\Delta v=\dfrac{10+12}{2}\times 2=22 $m/s,D正确.
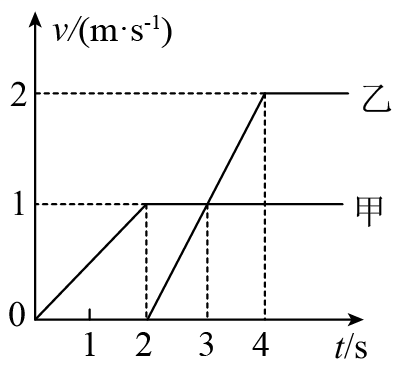
在人工智能机器人跑步比赛中,t=0时两机器人位于同一起跑线上,机器人甲、乙运动的速度-时间图像如图所示,则下列说法正确的是( )
- 机器人乙起跑时,机器人甲正好跑了2m
B.机器人乙从起跑开始,经3s后刚好追上机器人甲
C.机器人甲、乙相遇之前的最大距离为4m
D.机器人乙超过机器人甲后,甲、乙可能再次相遇
展开答案
【答案】B
【详解】
A.根据v—t图像与t轴所围面积表示位移,可知机器人乙在时起跑,t=2s此时,机器人甲跑过的距离
$x=\dfrac{1 \times 2}{2}=1m$
选项A错误;
B.机器人乙起跑3s后,甲通过的位移
$x=\dfrac{5+3}{2}\times 1=4m$
乙通过的位移
$x=\dfrac{1+3}{2}\times 2=4m$
可知
$x_甲=x_乙$
说明机器人乙追上甲,选项B正确;
C.两机器人在速度相等(即t=3s)时相距最远,两者间的最大距离等于0~3s内的位移之差,则
$x_{max}=\dfrac{1 \times 2}{2}m+\dfrac{1\times 1}{2}=1.5m$
选项C错误;
D.机器人乙超过机器人甲后,乙的速度总比甲的大,则甲、乙不可能再次相遇,选项D错误。
小球从某一高度自由落下,落到水平桌面后反弹回到原高度,如此数次落下和反弹,取竖直向下为正方向,下列速度v和位移x的关系图象中能描述该过程的是( )
展开答案
【答案】D
【解析】以竖直向下为正方向,则小球下落时的速度为正值,小球下落的过程中,根据运动学公式有
$v^2=2gx$
由数学知识可得,v-x图象应是抛物线,小球与地面碰撞后上升的过程,速度为负值,与下落过程具有对称性。
故选D。
(2020·四川双流中学模拟)在一大雾天,一辆小汽车以30 m/s的速度行驶在高速公路上,突然发现正前方30 m处有一辆大卡车以10 m/s的速度同方向匀速行驶,小汽车紧急刹车,刹车过程中刹车失灵.如图所示,a、b分别为小汽车和大卡车的v t图线,以下说法正确的是 ( )
A.因刹车失灵前小汽车已减速,不会追尾
B.在t =5 s时追尾
C.在t =3 s时追尾
D.由于初始距离太近,即使刹车不失灵也会追尾
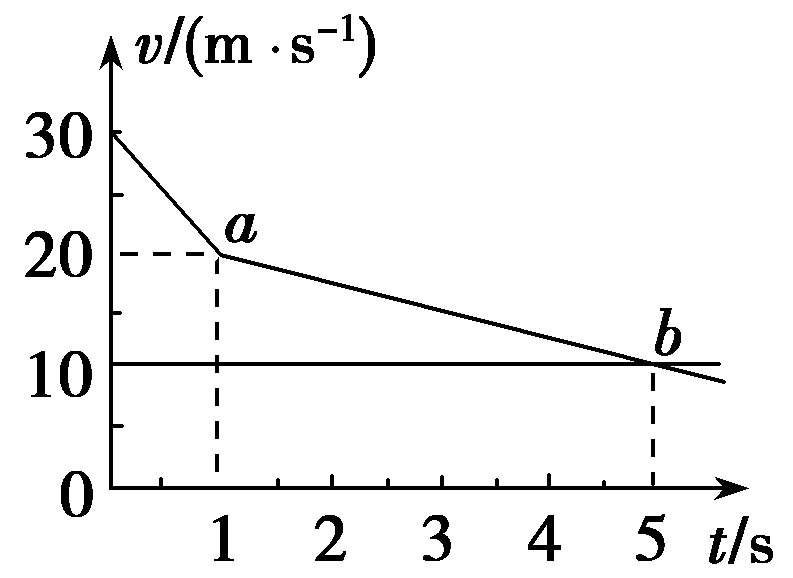
展开答案
【答案】:C
【解析】:由图象可知,在t=5 s时,两车的速度相等,若此时小汽车与大卡车没有追尾,则以后再不会发生追尾,由v t图象与坐标轴所围图形的面积表示位移的大小可得:t=5 s时,xa-xb=35 m,t=3 s时,xa-xb=30 m,所以在t=3 s时,小汽车与大卡车出现了追尾,C正确,A、B错误;如果刹车不失灵,则两车在t=2 s时共速,此时xa-xb=20 m<30 m,故不会追尾,D错误.
(2020·皖江名校模拟)小明和小华操控各自的玩具赛车甲、乙在小区平直的路面上做直线运动,t=0时刻两赛车恰好并排,此后两赛车运动的位移x与时间t的比值随时间t的关系如图所示,对于甲、乙两赛车前2 s的运动,下列说法正确的是 ( )
A.t=1 s时,甲在乙的前面且相距最远
B.t=1 s时,甲、乙两赛车相遇
C.t=2 s时,甲在乙的前面且相距最远
D.t=2 s时,甲、乙两赛车相遇
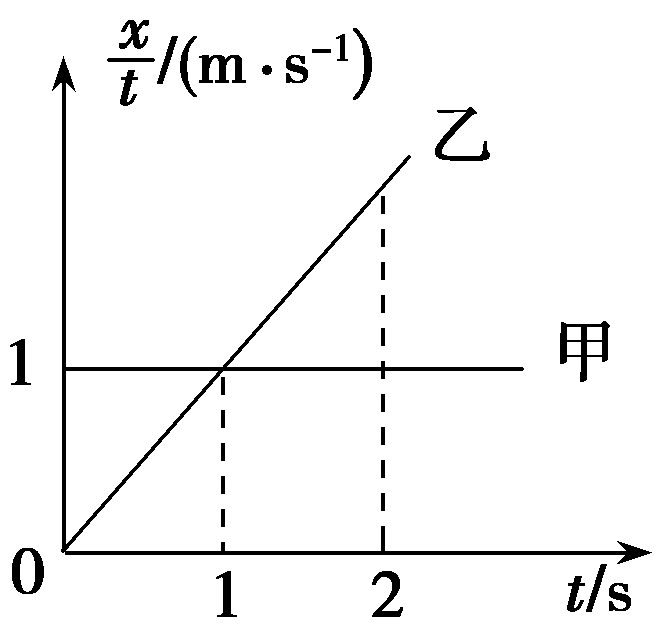
展开答案
【答案】:B
【解析】:典型的函数题型,找出横坐标和纵坐标的函数关系。
甲赛车$\dfrac{x}{t}$恒定不变,故做匀速直线运动,速度为v_甲=1 m/s.根据$x=v_0t+\dfrac{1}{2}at^2$可得$\dfrac{x}{t}=\dfrac{1}{2}at+v0$可知乙赛车初速度为零,加速度为a=2 m/s2,故两质点在t=0.5 s时速度相等,此时两者相距最远;当两者相遇时$v_甲t+\dfrac{1}{2}at^2$,解得t=1 s,甲、乙相遇,此后乙的速度大于甲的速度,乙在甲的前面,B正确.
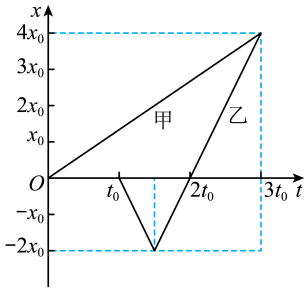
甲、乙两个足球从同一位置沿同一直线被先后击出,运动位移—时间图像如图所示,则( )
A.1.5t0时甲的速度大于乙的速度
B.2.5t0时甲的加速度大于乙的加速度
C.3t0时乙恰好与甲相碰
D.1.5t0-3t0内两球的平均速度相等
展开答案
【答案】C
【解析】A.在x-t图像中,斜率表示速度的大小,由图可知甲的斜率
$K_甲=\dfrac{4x_0}{3t_0}$
乙在1.5to时的斜率为
$K_乙=\dfrac{2x_0}{0.5t_0}=\dfrac{4x_0}{t_0}$
可得1.5to时甲的速度小于乙的速度,故A错误;
B.甲和乙都是做匀速运动,故加速都为0,故B错误;
C.在3to时,甲乙的位移都为4x0,故3to时乙恰好与甲相碰,故C正确;
D.由图可知,1.5to-3to内甲球的位移小于乙球,故甲的平均速度小于乙球的平均速度,故D错误。
甲.乙两物体从同一地点同时开始沿同一方向运动,甲物体运动的v﹣t图象为两段直线,乙物体运动的是v﹣t图象为两段半径相同的$\dfrac{1}{4}$圆弧曲线,如图所示,图中t4=2t2 , 则在0﹣t4时间内,以下说法正确的是( )
A.甲物体的加速度不变
B.乙物体做曲线运动
C.两物体t1时刻相距最远,t4时刻相遇
D.甲物体的平均速度等于乙物体的平均速度
展开答案
【答案】D
【解析】解:
A、速度时间图线的斜率表示加速度,则知甲的加速度是变化的,故A错误。
B、速度图象不是物体的运动轨迹,乙做的是变速直线运动,故B错误。
C、图线与时间轴围成的面积表示位移,相距的距离等于两者位移之差,根据图象可知,t3时刻相距最远,t4时刻相遇,故C错误。
D、0﹣t4时间内甲物体的位移等于乙物体的位移,时间相等,则平均速度相等,故D正确。
