质点的直线运动经典例题
附带计算过程,所有图片都是LaTeX代码绘制
质点的直线运动例题
(2021·全国甲卷·14)如图,将光滑长平板的下端置于铁架台水平底座上的挡板P处,上部架在横杆上.横杆的位置可在竖直杆上调节,使得平板与底座之间的夹角θ可变.将小物块由平板与竖直杆交点Q处静止释放,物块沿平板从Q点滑至P点所用的时间t与夹角θ的大小有关.若由30°逐渐增大至60°,物块的下滑时间t将( )
A.逐渐增大
B.逐渐减小
C.先增大后减小
D.先减小后增大
展开答案
【答案】D
【解析】方法1:设PQ的水平距离为L,由运动学公式可知$\frac{L}{cos\theta}=\frac{1}{2} sin \theta t^2$,可得$t^2=\frac{4L}{gsin2\theta }$。θ=45°时t有最小值,故当θ由30°逐渐增大至60°,物块的下滑时间t先减小后增大。
方法2:还记得等时圆模型吧,显然A、B落地的时间一样,那肯定是先减小再增大。
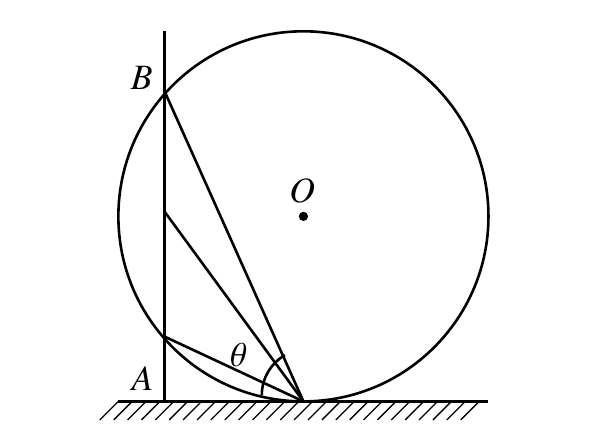
质点做直线运动的位置x与时间t的关系为$x=6+5t+t^2$ (各物理量均采用国际单位制单位),则该质点 ( )
A.第1 s内的位移是12 m
B.前2 s内的平均速度是7m/s
C.任意相邻的1 s内位移差都是2m
D.任意1 s内的速度增量都是2 m/s
展开答案
【答案】BCD
【解析】
这题很怪,和平时刷的题不同,因为多了一个6,使得无从下手。这其实就是出题人故意折磨人而已,本人极其厌恶这样出题,科技的发展向来都是靠寻一个又一个当下最简单有效的解决方案,从来没见过有谁故意提高难度解决问题的,如果有那一定会被淘汰。这道题一定要仔细研究,亲自计算两种方案,知道数据完全正确,计算力往往就是细心的体现。解法1:做题先思考,如果能发现“位置”而不是“位移”,并且$x=6+5t+t_2$ 与 $x=5t+t_2$式子的不同,应该能意识到6是始坐标而已,初始速度是5m/s,加速度是2m/s2,余下计算和6没什么关系。
A、第一秒内的位移是$x=5t+t_2=5 \times 1s +1=6 $ 错误
B、前2s内的平均速度等于就是第1s末速度,$v_1=5m/s +2m/s^2 \times1s=7m/s $,当然也可以平均值 $x_2=(6+5\times2+4)m-6m=14m$,$v=\frac{x_2}{t_2}=\frac{14}{2}=7m/s$ 正确
C.加速度为$2m/s^2$的位移表达为$x=t^2$,相同时间位移差自然就是2m。正确
D.加速为2$m/s^2$正确。
解法2:
解决问题的方法永远不可能只有一种,如果陷入某个思维不能自拔,不如跳出来,直接列出来。$x=6+5t+t_2$ 把时间带进去,画一个坐标即可。
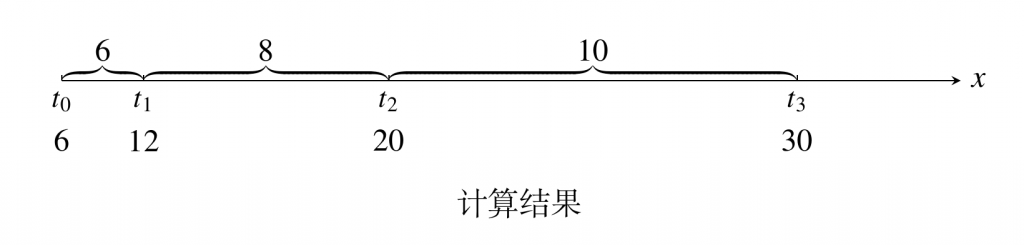
A、第一秒内的位移差是6m
B、周期是1,前两秒位移(8+6)÷2=7 m/s
C、位移差是2m
D、$\Delta x =at^2 \quad \Delta x =2 $解得a=2m/s2
(2019·广东深圳市·红岭中学高考模拟)如图所示是一做匀变速直线运动的质点的位置–时间图象(x–t图象),P(t1,x1)为图象上一点.PQ为过P点的切线,与x轴交于点Q(0,x2).已知t=0时质点的速度大小为v0,则下列说法正确的是
A.t1时刻,质点的速率为$\frac{x_1}{t_1}$
B.t1时刻,质点的速率为$\frac{x_2}{t_1}$
C.质点的加速度大小为$\frac{x_1-x_2}{t^2}-\frac{v_0}{t_1}$
D.质点的加速度大小为$\frac{x_1-x_2}{t-1^2}$
展开答案
【答案】 C
【解析】
$x–t $图象的斜率表示速度,则$t_1$时刻,质点的速率为$\frac{x_1-x_2}{t^2}$,根据加速度定义$a=\frac{\Delta v}{\Delta t}= \frac{v-v_0}{t_1} = { \frac{x_1-x_2}{t_1}-v_0 \over t_1}=\frac{x_1-x_2}{t^2}-\frac{v_0}{t_1}$
没有思路的时候就去找定义,从定义出发用简单的逻辑去整理,所有的学生一定要自己推算到正确!取一根长2m左右的细线,5个铁垫圈和一个金属盘,在线端系上第一个垫圈,隔12cm再系一个,以后垫圈之间的距离分别为36cm,60cm,84cm,如图所示,站在椅子上,向上提起线的上端,让线自由垂下,且第一个垫圈紧靠放在地面上的金属盘内,松手后开始计时,若不计空气阻力,则第2、3、4、5各垫圈( )
A.落到盘上的声音时间间隔相等
B.落到盘上的声音时间间隔越来越大
C.依次落到盘上的速率关系为 $1:\sqrt{2}:\sqrt{3}:2$
D.依次落到盘上的时间关系为$1:(\sqrt{2}-1):(\sqrt{3}-\sqrt{2}):(2-\sqrt{3})$
展开答案
【答案】A
【解析】5个铁垫圈同时做自由落体运动,下降的位移之比为1:3:5:7.可以看成一个铁垫圈自由下落,经过位移之比为1:3:5:7.因为初速度为零的匀加速直线运动在相等时间内的位移之比为1:3:5:7,知各垫圈落到盘中的时间间隔相等,故A正确
甲、乙两辆车沿平直公路从某地同时驶向同一目标,甲车在前一半时间内以速度$v_1$做匀速直线运动,后一半时间内以速度$v_2$做匀速直线运动;乙车在前一半路程内以速度$v_1$做匀速直线运动,后一半路程内以速度$v_2$做匀速直线运动,则( )
A.甲先到达 B.乙先到达 C.甲乙同时到达 D.不能确定
展开答案
【答案】 A
【解析】方法1:分析甲车运动情况:设甲车所用时间为t,前一半的位移为$x_1$,后一半位移为$x_2$,则$x_1=v_1\times\frac{t}{2}$,$x_2=v_2\times\frac{t}{2}$,由平均速度公式得$v_{\text{甲}}=\frac{v_1+v_2}{2}$。分析乙车运动情况:设整段位移为x,前一半位移用时为$t_1$,由位移公式x=vt得,前半段位移用时为$t_1=\frac{x}{2v_1},t_2=\frac{x}{2v_2}$,由平均速度公式得$v_y=\frac{x}{t_1+t_2}=\frac{2v_{1}v_{2}}{v_{1}+v_{2}}$。又因为$$ V_{\text{甲}} – v_{\text{乙}}=\frac{v_1+v_2}{2}-\frac{2v_{1}v_{2}}{v_{1}+v_{2}}=\frac{(v_1-v_2)^2}{2(v_1+v_2)}>0$$,所以甲先到。
方法2:甲图前后时间一样,平均速度等于$v=\frac{v_1+v_2}{2}$,乙图中可以在$v_1$过程中截取一段时间和$v_2$过程相等,那么$2t_0$这段时间的平均速度和甲一样,余下部分的速度肯定小于$v=\frac{v_1+v_2}{2}$,所以平均速度必然小于甲。
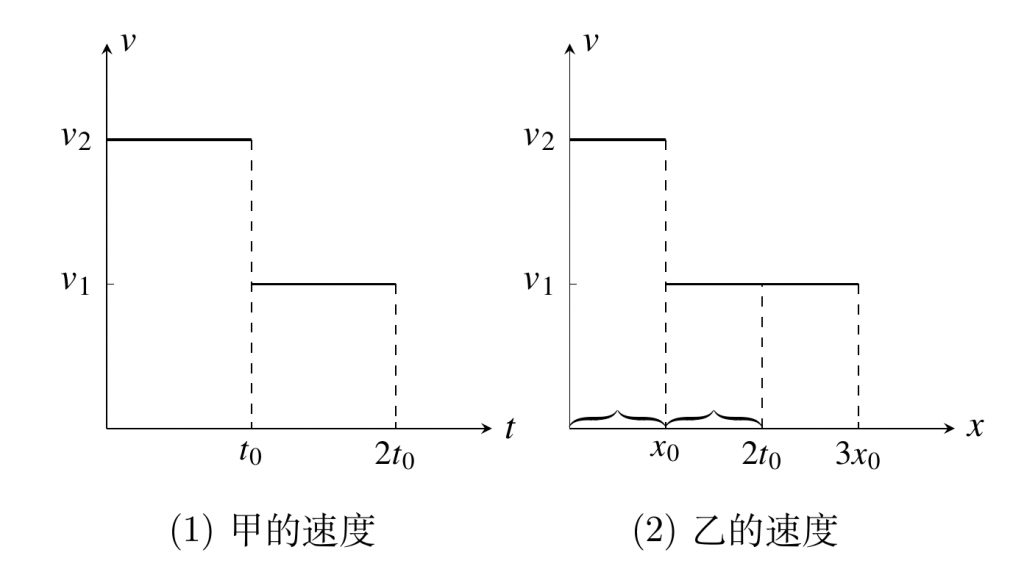
方法3:直接赋值计算,碰到任何问题都要多想一下,肯定会有答案。
一物体在做匀加速直线运动,通过一段大小为15m的位移所用的时间为5s,紧接着通过下一段大小为15m的位移所用的时间为3是,则物体运动的加速度大小为()
A、5m/s B、3m/s C、2m/s D、0.5m/s
展开答案
【答案】 D
【解析】
画图是解决直线运动题的法宝,画一条直线,上面写距离,下面标时间,平均速度等于中间时刻速度,$\bar v_1 =\frac{15}{5}=3$,$\bar v_2 =\frac{15}{3}=5$,
$$a=\frac{\Delta v}{\Delta t} = \frac{5m/s-2m/s}{2.5s+1.5s}=0.5m/s$$

(2021·山东济南市高三期末)伽利略在研究匀变速直线运动规律时,让小球从斜面的不同位置自由滚下,观测出小球从不同起点运动到底端的位移x与所对应的时间t,画出x-t2图象.设小球运动的加速度为a,则图象的斜率为( )
A. $\frac{1}{2}a^2$ B.a C.$\frac{1}{a} $ D.$\frac{2}{a}$
展开答案
【答案】 A
【解析】
很多高中题目专门把人往傻的方向逼,这种思维在现实中往往没有任何用处,为了适应这些sb不得不去适应,这就是其中一种体现,我们可以适应,但是这绝不是真理。小球从静止开始沿斜面向下做匀加速运动,位移—时间关系为$x=\frac{1}{2}at^2$,即x与$t^2$成正比,所以$x-t^2$图象是一条过原点的直线,直线的斜率为2a.故选A.
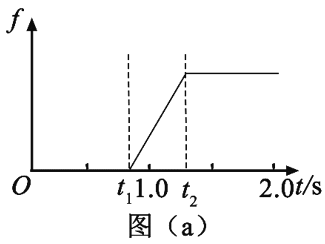
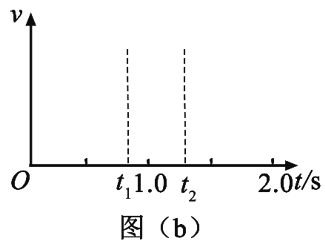
一质量为m=2000 kg的汽车以某一速度在平直公路上匀速行驶.行驶过程中,司机忽然发现前方100 m处有一警示牌.立即刹车.刹车过程中,汽车所受阻力大小随时间变化可简化为图(a)中的图线.图(a)中,0~t1时间段为从司机发现警示牌到采取措施的反应时间(这段时间内汽车所受阻力已忽略,汽车仍保持匀速行驶),t1=0.8 s;t1~t2时间段为刹车系统的启动时间,t2=1.3 s;从t2时刻开始汽车的刹车系统稳定工作,直至汽车停止,已知从t2时刻开始,汽车第1 s内的位移为24 m,第4 s内的位移为1 m.
(1)在图(b)中定性画出从司机发现警示牌到刹车系统稳定工作后汽车运动的v-t图线;
(2)求t2时刻汽车的速度大小及此后的加速度大小;
(3)求刹车前汽车匀速行驶时的速度大小及t1~t2时间内汽车克服阻力做的功;司机发现警示牌到汽车停止,汽车行驶的距离约为多少(以t1~t2时间段始末速度的算术平均值替代这段时间内汽车的平均速度)?
【解析】
这是一个非常经典的题,一种最后一秒内就已经停止的模型。(1)
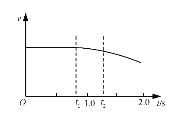
(2)先判断一下是不是正好最后一秒正好停止。
右图很明显可以看出,最后一秒没到重点就已经停止了。
逆向思维是学习物理,乃至生活中都非常有用的一种思维方式,可以大大简化问题,让事物变成我们熟悉的直觉去解释。根据题意,我们可以轻松的画出时间轴。
我们假设0-1s的时间差值为$\Delta t$
$\frac{1}{2}a\Delta t^2=1$
$v_0 t+\frac{1}{2}at^2=24$
$v_0=(\Delta t+2)a$
多数人都可以列出这个等式,但是无法解出来,我们要求的是a,所以只需要把$t=\sqrt{\frac{2}{a}}$带入,最终得到。
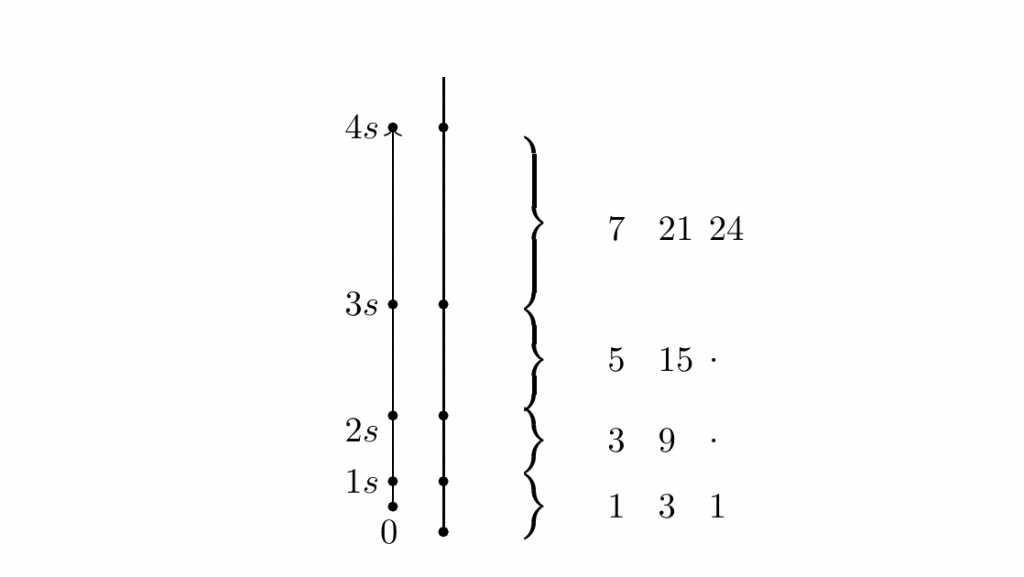
$$2\sqrt{2a}+5a=48$$
计算力强的或许可以算出来,不强的就懵逼了,其实我们可以靠直觉,想想看,这是物理题不是数学,它不会考你数学的计算力的,既然48是整数,那么根号下的一定是整数,猜一下也知道$a=8m/s$,$v2=28 m/s$
(3)设汽车的刹车系统稳定工作时,汽车所受阻力的大小为$f$,由牛顿定律有:$f=ma$在t1~t2时间内,阻力是均匀变化的,所以取平均值,对汽车冲量的大小为:
$I=\frac{1}{2}(t_1-t_2)$
由动量定理有:$I=\Delta p=mv_1-mv-2$
由动能定理,在t1~t2时间内,汽车克服阻力做的功为:$W=\frac{1}{2}mv_1^2-\frac{1}{2}mv_2^2$
联立,代入已知数据解得
v1=30 m/s⑬
$W=1.16\times10^5$
从司机发现警示牌到汽车停止,汽车行驶的距离s约为
$$s=v_1t_1+\frac{1}{2}(v_1+v_2)(t_2-t_1)+\frac{v_2^2}{2a}$$
代入已知数据解得
s=87.5 m
一个小球从O点由静止开始做匀加速运动,PQ、QN时间相等,PQ距离2m,QN距离5m,求OP的距离?
展开答案
【答案】 $\dfrac{1}{24}$
【解析】
$Delta X = at^2$
$5-2=at^2$
PN的平均速度等于Q点的瞬时速度:
$v = \dfrac{2+5}{2t}$
$v^2=2ax$
$OP=x-2$
解得:OP=$\dfrac{1}{24}$
一辆汽车由静止开始做初速度为零的匀加速直线运动,速度增大到25m/s后做匀速直线运动,已知汽车前5s内的位移为75m,则汽车匀加速运动的时间为( )
A.3s B.4s C.5s D.6s
展开答案
【答案】B
【解析】:方程思维最简单,假设加速度为a,匀加速时间为t,列等式之前一定要进行简单的判断,如果5s一直加速,x=25/2×5=62.5.所以一定有一段是匀加速。则可列等式,
$25(5-t)+\frac{1}{2}25t=75$
t=4s 故选.B
如图,调整水龙头的开关,使单位时间内流出水的体积相等。水由于重力作用,下落速度越来越大,水柱越来越细。若水柱的横截面可视为圆,图中a、b两处的横截面直径分别为0.8cm和0.6cm,则经过a、b的水流速度之比为()
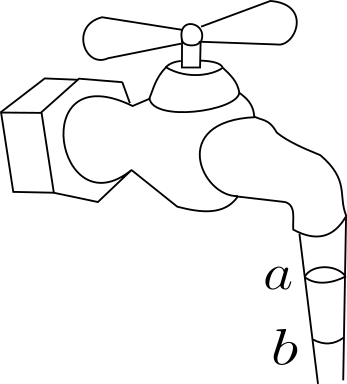
A、1:3 B、1:9 C、3:4 D9:16
展开答案
【答案】D
【解析】由于相同时间内通过任一横截面的水的体积相等,取一段极短的时间1,对两个不同的截面的瞬时速度,就会变成这段体积的平均速度!
$v_a t S_a=v_b t S_b$
$s_a =\pi r^2$
所以选D
