空间
空间是与时间相对的一种物质客观 存在形式,但两者密不可分,按照宇宙大爆炸理论,宇宙从奇点爆炸之后,宇宙的状态由初始的“1”分裂开来,从而有了不同的存在形式、运动状态等差异,物与物的位置差异度量称之为“空间”,空间由长度、宽度、高度、大小表现出来。位置的变化则由“时间”度量。
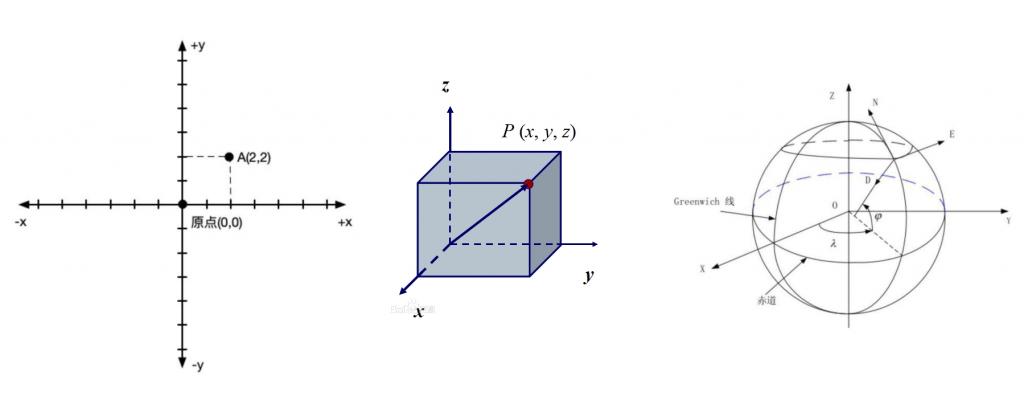
物体存在、运动的(有限或无限的)场所,即三维区域,称为(三维)空间,那么我们该怎么描述这个空间呢?希腊数学家欧几里得已经帮我们建立了一个空间秩序,那就是欧式几何空间,高中的题目都在欧式几何空间。
《几何原本》是古希腊数学家欧几里得创作的一部数学著作,成书于公元前300年左右。
这是一部非常伟大的书,它建立了一种数学研究的机制,这种机制也坚定了数学的研究基础。
理解这一点非常有助于你学习数学。
首先,《几何原本》建立了比较严密的几何体系,其诞生标志着几何学已成为一个有着比较严密的理论系统和科学方法的学科,在几何学发展史上具有划时代的意义。在这个体系中有四个方面的内容:
①定义。亦即几何学里用的名称或术语的意义,都是以生产实践中抽象出来且为人们所共知的,因而无需加以说明。例如“点”的定义是:点只有位置而没有大小,且不能被分割。
②公理。亦即不加逻辑推证而自明的真理。
③公设。就是几何学中假设其成立的事项,但这种假设必须有客观依据而被大家公认。例如,过任何不同的两点,可以作一条直线。近代的学者不再把公设与公理分开,而统称之为公理。
五大公理公设
公设
1.1 过两点可以作一条直线。
1.2 直线可以向两端无限延伸。
1.3 以定点为圆心及定长的线段为半径可以作圆。
1.4 凡直角都相等。
1.5 同平面内一条直线和另外两条直线相交,若在直线同侧的两个内角之和小于180°,则这两条直线经无限延长后在这一侧一定相交。(等价与:过直线之外一点有唯一的一条直线和已知直线平行)
公理
1.1 等于同量的量彼此相等。
1.2 等量加等量,其和仍相等。
1.3 等量减等量,其差仍相等。
1.4 彼此能够重合的物体是全等的。
1.5 整体大于部分。
④命题。包括作图题和定理两部分。作图题是从几何学里已知的对象出发,找出或作出所要求的对象;定理则是根据假定、公理、公设和定义,应用逻辑推理方法推证而得出的结论。
全书就是以第1卷的定义、公设、公理为依据,逻辑地展开各部分内容。比如之后出现的每一个定理,都写明什么是已知的、什么是要求证的,都根据前面的定义、公设、公理、定理等进行逻辑推理给予严格的证明。
其次,欧几里得在《几何原本》中把几何学建筑在最初的公设、公理的基础上,然后运用逻辑的定义和推理方法依次导出后面的定义和定理,把庞大的零散的几何知识用逻辑的链子整理和编织成为一个系统的概念和理论的完整体系,并规定了几何的证明方法(如分析法、综合法和归纳法等),这是用公理方法建立几何体系的雏形,对近代数学的发展有着巨大的推动作用,给现代几何学打下了坚实的基础。

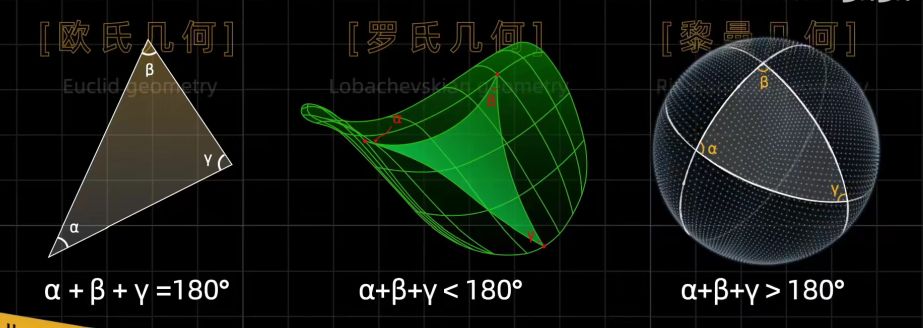
除了欧式几何,还有黎曼几何、罗氏几何。
他们都是各自发展的,建立在不同的公设的前提下推理的。
黎曼几何中的一条基本规定是:在同一平面内任何两条直线都有交点(等价于平行线相交)。它的另一条公设讲:直线可以无限延长,但总的长度是有限的,黎曼几何的模型是一个经过适当“改进”的球面。
罗氏几何规定:垂直于同一直线的两条直线,当两端延长的时候,离散到无穷。罗氏几何的模型是一个双曲面。
欧氏几何(平直空间)、罗氏几何(马鞍形)、黎曼几何(球形)是三种各有区别的几何。这三种几何各自所有的命题都构成了一个严密的公理体系,各公理之间满足和谐性、完备性和独立性。因此这三种几何都是正确的。
非欧几何学的出现,开阔了人们的眼界,由于存在与欧氏几何系统不同的非欧几何学系统,于是几何学及空间有了新的含义。

高中阶段只研究平直时空,不会用黎曼几何解决更复杂的问题,所以各位同学需要理解如何通过简单的数学构建物理的大厦,如同欧几里得一样。
想学好物理就要描述空间,这也是高中开始为什么先要讲质点,测量,位移、矢量等等,其实就是做一个规范,在统一的规范下面研究物理。