计算题和实验经典例题
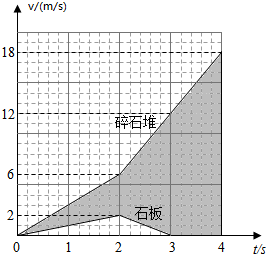
下暴雨时,有时会发生山体滑坡或泥石流等地质灾害.某地有一倾角为θ=37°(sin37°=35)的山坡C,上面有一质量为m的石板B,其上下表面与斜坡平行;B上有一碎石堆A(含有大量泥土),A和B均处于静止状态,如图所示.假设某次暴雨中,A浸透雨水后总质量也为m(可视为质量不变的滑块),在极短时间内,A、B间的动摩擦因数μ1减小为$\dfrac{3}{8}$,B、C间的动摩擦因数μ2减小为0.5,A、B开始运动,此时刻为计时起点;在第2s末,B的上表面突然变为光滑,μ2保持不变.已知A开始运动时,A离B下边缘的距离L=27m,C足够长,设最大静摩擦力等于滑动摩擦力.取重力加速度大小g=10m/s2.求:
(1)在0~2s时间内A和B加速度的大小
(2)A在B上总的运动时间.
展开答案
分析
(1)对A、B受力分析,根据牛顿第二定律可以求出加速度的大小;
(2)根据A、B的加速度的大小,利用速度时间的关系式和它们之间的距离可以计算时间的大小.
解答(1)在0~2s时间内,A和B的受力如图所示,
其中$f_1$、$N_1$是A与B之间的摩擦力和正压力的大小,$f_2$、$N_2$是B与C之间的摩擦力和正压力的大小,方向如图所示.
由滑动摩擦力公式和力的平衡条件得
$f_1=\mu_1N_1 $①
$N_1=mgcos\theta $ ②
$f_2=\mu_2N_2$ ③
$N_2=N_1+mgcos\theta$ ④
规定沿斜面向下为正,设A和B的加速度分别为a1和a2,
由牛顿第二定律得
$mgsin\theta-f_1=ma_1$ ⑤
$mgsin\theta+f_1-f_2=ma_2$ ⑥
联立①②③④⑤⑥式,并代入题给的条件得
$a_1=3m/s^2$ ⑦
$a_2=1m/s^2$⑧
2)在$t_1=2s$时,设A和B的速度分别为$v_1$和$v_2$,则
$v_1=a_1t_1=6m/s $ ⑨
$v_2=a_2t_1=2m/s $ ⑩
t>t1时,设A和B的加速度分别为a1′和a2′,此时A与B之间摩擦力为零,
同理可得:
$a_1’=6m/s^2$⑪
$a_2’=-2m/s^2$⑫
即B做减速运动.
设经过时间t2,B的速度减为零,则有
$v_2+a_2′ t_2=0$⑬
联立⑩⑫⑬式得
$t_2=1s$
在$t_1+t_2$时间内,A相对于B运动的距离为
$s=(\dfrac{1}{2}a_1t_1^2+v_1t_2+\dfrac{1}{2}a_1’t_2^2)−(\dfrac{1}{2}a_2t_1^2+v_2t_2+\dfrac{1}{2}a_2’t_2^2)
=12m<27m$
此后B静止不动,A继续在B上滑动.
设再经过时间t3后A离开B,则有
$l-s=(v_1+a_1’t_2)t_3+\dfrac{1}{2}a_1’t_3^2$
可得
$t_3=1s$(另一解不合题意,舍去)
设A在B上总的运动时间为t总,有
$t_总=t_1+t_2+t_3=4s$
一物体可视为质点,做匀减速直线运动,第一秒内运动32米,最后一秒内运动1米,问加速度是多少。
展开答案
【答案】8m/s2
【解析】难点在于一般人无法判断是不是最后一秒结束,这个可以按照1 3 5 7 9 ,对比即可。
假设最后一秒内t秒就停止了,然后画出图形,
$\dfrac{1}{2}at^2=1$
$(at+3a)\cdot 1+\dfrac{1}{2}a1^2=32$
$2 \sqrt{2a} +7a=64$
$a=8$
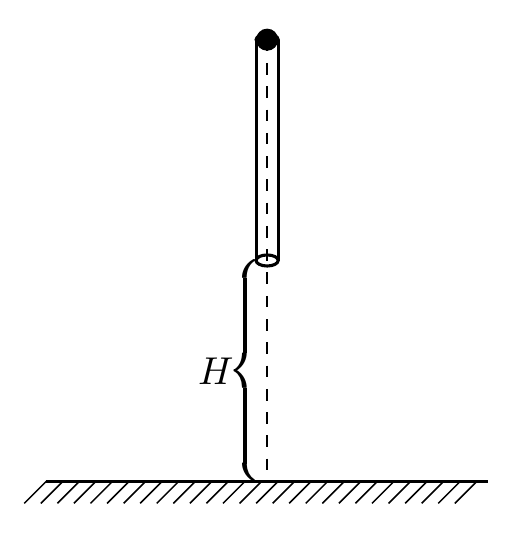
如图所示,一个质量为M长为L的圆管竖直放置,顶端塞有一个质量为m的弹性小球,M=4m,球和管间的滑动摩擦力和最大静摩擦力大小均为4mg.管从下端离地面距离为H处自由落下,运动过程中,管始终保持竖直,每次落地后向上弹起的速度与落地时速度大小相等,不计空气阻力,重力加速度为g.求:
(1)管第一次落地弹起时管和球的加速度;
(2)管第一次落地弹起后,若球没有从管中滑出,则球与管达到相同速度时,管上升的最大高度。
(3)管第二次弹起后球不致滑落,L应满足什么条件.
展开答案
(1)管第一次落地弹起时,管瞬间向上运动,受到自身重力以及摩擦力,所以管的加速度
$a_1=\dfrac{4mg+4mg}{4m}=2g$方向向下。
球受到向上的摩擦力和向下的重力,球加速度
$a_2=\dfrac{f-mg}{m}=\frac{4mg-mg}{m}=3g$方向向上。
(2)取竖直向下为正方向.球与管第一次碰地时速度$v_0=\sqrt{2gH}$ ,方向向下.碰地后管的速度$v_1=- \sqrt{2gH}$,方向向上;球的速度$v_2=\sqrt{2gH}$,方向向下若球刚好没有从管中滑出,设经过时间$t_1$,球管速度v相同,则有
$-v_1+a_1t_1=v_2-a_2 {t_1}^2$
$-\sqrt{2gH}-2gt_1=\sqrt{2gH}+3mgt_1$
$2\sqrt{2gH}=5mgt_1$
$t_1=\dfrac{2}{5}\sqrt{\dfrac{2H}{g}}$
此时管下端的高度为$h_1=v_0 t_1-\dfrac{1}{2} {a_1} {t_1}^2$ 带入数据
$h_1=\dfrac{12}{25}H$
此后管和球共速上升$v_g=v_0-a_2 t_1=\dfrac{1}{5} \sqrt{2gH}$
共速上升的高度 $h_2=\frac{v_g ^2}{2g}=\dfrac{1}{25}H$
管上升的最大高度$H_1$ $H_1=h_1+h_2=\dfrac{13}{25}H $
(3)设第一次弹起过程中球相对于管的位移$x_1$,在管开始下落到上升到$H_1$的过程中,由动能减少量等于摩擦力做功
$Mg(H-H_1)+mg(H-h_1 + x_1)-4mg x_1=0$$
$x_1= \dfrac{4}{5}H_1$
即L应满足条件$x_1 +x_2 \leq L$
$\dfrac{4}{5}H +\dfrac{4}{5}H_1\leq L$
$\dfrac{4}{5}H +\dfrac{4}{5} \dfrac{13}{25}H\leq L$
$\dfrac{152}{125}H\leq L$
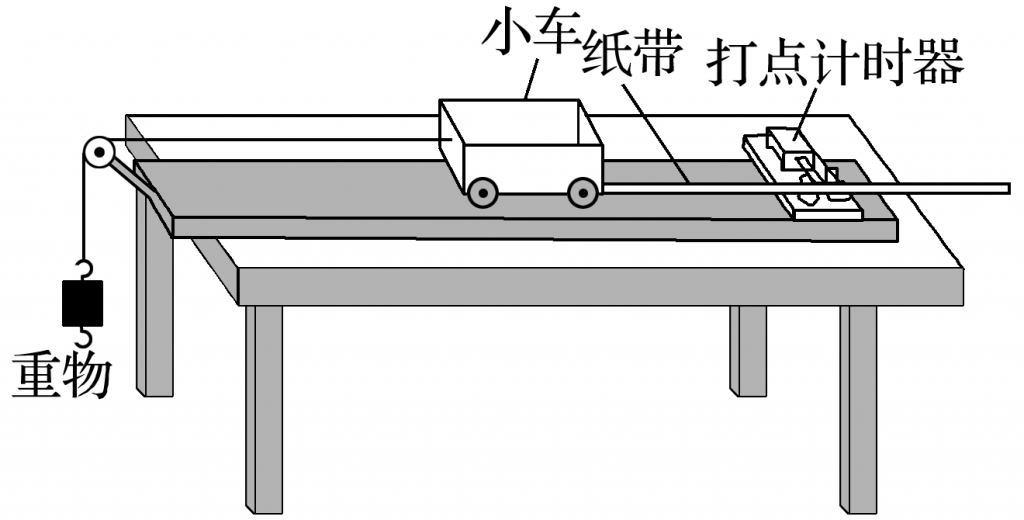
(北京卷·21改编)用图所示的实验装置研究小车速度随时间变化的规律.
主要实验步骤如下:
a.安装好实验器材,接通电源后,让拖着纸带的小车沿长木板运动,重复几次.
b.选出一条点迹清晰的纸带,找一个合适的点当作计时起点O(t=0),然后每隔相同的时间间隔T选取一个计数点,如图中A、B、C、D、E、F……所示.
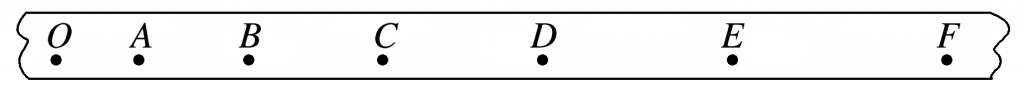
c.通过测量、计算可以得到在打A、B、C、D、E……点时小车的速度,分别记作v1、v2、v3、v4、v5……
d.以速度v为纵轴、时间t为横轴建立直角坐标系,在坐标纸上描点,如图所示.
结合上述实验步骤,请你完成下列任务:
(1)在下列仪器和器材中,还需要使用的有________和________(填选项前的字母).
A.电压合适的50Hz交流电源
B.电压可调的直流电源
C.刻度尺
D.秒表
E.天平(含砝码)
(2)在图象中已标出计数点A、B、D、E对应的坐标点,请在该图中标出计数点C对应的坐标点,并画出v-t图象.
(3)观察v-t图象,可以判断小车做匀变速直线运动,其依据是________________.v-t图象斜率的物理意义是__________________.
(4)描绘v-t图象前,还不知道小车是否做匀变速直线运动.用平均速度Δt表示各计数点的瞬时速度,从理论上讲,对Δt的要求是________(选填“越小越好”或“与大小无关”);从实验的角度看,选取的Δx大小与速度测量的误差________(选填“有关”或“无关”).
展开答案
【答案】 (1)A C (2)如图所示
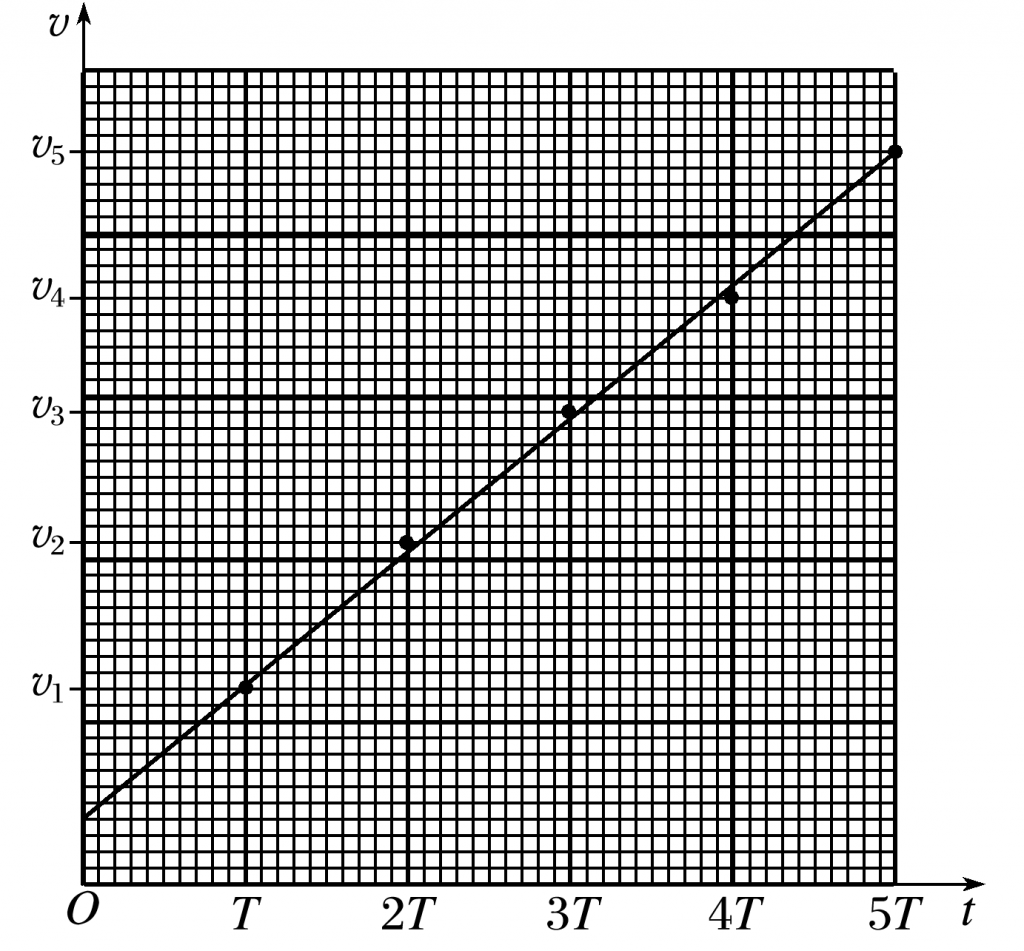
(3)小车的速度随时间均匀变化 加速度 (4)越小越好有关
【解析】 (1)打点计时器使用的是交流电源,故选A,不选B;相邻打点间的时间是已知的,故不选D;计数点间的距离需要用刻度尺测量,故选C;由于不需要知道小车和重物的质量,故不需要天平(含砝码),故不选E.
(2)连线时要让尽量多的点在一条直线上.
(3)可以依据v-t图象是倾斜的直线(斜率一定),即小车的速度随时间均匀变化,判断出小车做匀变速直线运动;v-t图象的斜率表示加速度.
(4)严格地讲,$\dfrac{\Delta x}{\Delta t}$表示的是Δt内的平均速度,只有当Δt趋近于0时,$\dfrac{\Delta x}{\Delta t}$才表示瞬时速度,因此若用$\dfrac{\Delta x}{\Delta t}$表示各计数点的瞬时速度,对Δt的要求是越小越好;从实验的角度看,选取的Δx越小,用$\dfrac{\Delta x}{\Delta t}$计算得到的平均速度越接近计数点的瞬时速度,但Δx过小,测量误差增大,因此选取的Δx大小与速度测量的误差有关.
