定义和公式

---

定义是普遍使用的逻辑方法，有三方面作用：一是综合作用，即通过定义把人们对事物的认识巩固下来，作为以后认识的基础；二是分析作用，即通过定义揭示一个语词或概念的内涵和外延，从而明确它们的使用范围，进而弄清楚某个语词或概念的使用是否恰当，有无逻辑错误；三是交流作用，即在理性的交谈和对话中，对所使用的概念获得共同的理解避免无谓争论，以提高人们交流的成功率。

物理学的定义更是精简，不但要知道定义的内容，更要知道为何要这么定义，这是学好物理的基础。

质点：用来代替物体的具有质量的物质点。

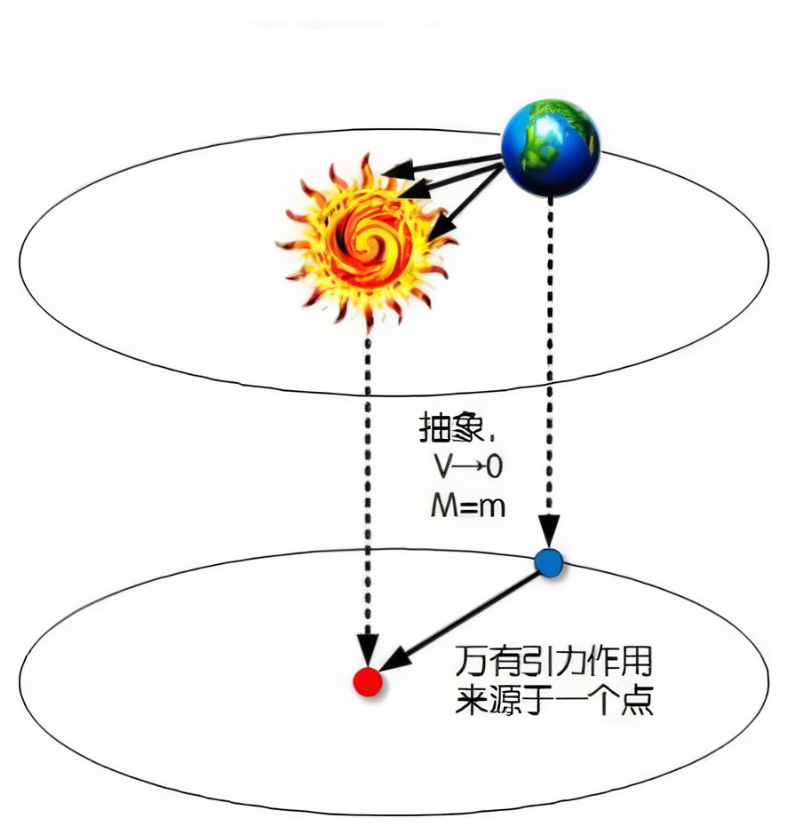
参考系：描述一个物体运动时，选来用作参考的物体叫参考系。

• 参考系的选择是一个重要的问题，选取得当会使问题的研究变得简单，方便。

位移：由初始位置指向末位置的有向线段。

时刻：是指某一时间轴上用一个点来表达，无长短意义，对应的是位置、瞬时速度、动量、能量等状态量。

时间：是两时刻间的间隔，在时间轴上用线段表示，对应的是位移、路程、平均速度、冲量、功等过程量。

速度：质点的位移与时间的比值。

速率：路程和时间的比值。

矢量：有大小有方向的物理量。

加速度：定义式： $a=\frac{ \Delta v}{ \Delta t}$ 决定式：$a=\frac{f}{m}$

---

本章公式非常多，对于学生的计算能力和思维转换要求非常高 ，开始学习时必须要对公式一一推导。

关键的公式 $S=vt$和$a=\frac{ \Delta v}{ \Delta t}$是这章所有公式起点，

$S=vt \rightarrow S=\frac{1}{2}at\times t $其中 $ \frac{1}{2}at$ 就是平均速度，平均化是高中物理常见方法。

$v=v_0+at $ 初速度基础上累积可得任意时间的速度。

$S=vt+ \frac{1}{2} at^2$

• 我们可以通过一道题目来得到一个 新的公式：已知初速度$v_0$末速度$v$，加速度a,那么位移X=？

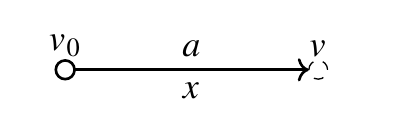
以$x=vt$为起始，只需要知道平均速度和时间就行了。一切推导忘记任何步凑，从起始点找即可。

$v=\dfrac{v+v_0}{2} $

$v=v_0+at $，$t=\dfrac{v-v_0}{a} $ 根据匀加速的特点轻松得到。

$x=\dfrac{v^2-v_0^2}{2a} $整理下$v^2-v^2=2ax$

假设中间位置速度，通过这个公式可以轻易得到 $v_{s/2} = \sqrt{\dfrac{v_0^2 + v_t^2}{2}}$

先定义$\Delta x $，有了标准才好统一讨论， $x_2 – x_1=\Delta x $ ，就是相邻时间间隔的位移差。

发现a=2的特殊情况下$\Delta x =2m $，$x_5-x_1=8m$ 是$\Delta x =2m $的四倍，可以总结出$x_m-x_n=（m-n）2，$，进一步扩大适用范围

$\Delta x =aT^2 $,可以顺利的得出 $x_m-x_n=(m-n)aT^2$

对于$\Delta x =aT^2 $的推导，学生需要自行尝试，方法就是 $\Delta x=x_n+1 – x_n$，用特数学方法表示任意相邻时间位移差值即可。

匀变速直线运动

平均速度：$\bar{v} = \dfrac{s}{t} = \dfrac{1}{2}(v_0+v_t)$

有用推论：$v_t^2 – v_0^2 = 2as$

中间时刻速度：$v_{t/2} = \bar{v} = \dfrac{1}{2}(v_0+v_t)$

末速度：$v_t=v_0 + at$

中间位置速度：$v_{s/2} = \sqrt{\dfrac{v_0^2 + v_t^2}{2}}$

位移：$s = v_0t + \dfrac{1}{2}at^2 = \bar{v}t = \dfrac{v_t}{2}t$

加速度：$a = \dfrac{v_t – v_0}{t}$

实验用推论：$\Delta S = aT^2$

$x_m-x_n=(m-n)aT^2$

$1m/s = 3.6km/h$

匀变速直线运动中连续相等的时间间隔内的位移差是一个恒量，设时间间隔为$T$，加速度为$a$，连续相等的时间间隔内的位移分别为：$S_1,S_2,\cdots S_N$，则有：$\Delta S = S_2 – S_1 = S_3 – S_2 = \cdots = S_N – S_{N-1} = aT^2$\

无论是匀加速还是匀减速，总有：$v_{t/2} < v_{s/2}$

初速度为零的匀加速直线运动

设$T$为时间单位，则有：

$1T$末、$2T$末、$3T$末、$\cdots$、$nT$末的瞬时速度之比：$v_1:v_2:v_3:\cdots :v_n = 1:2:3:\cdots :n$

$1T$末、$2T$末、$3T$末、$\cdots$、$nT$末的位移之比：$s_1:s_2:s_3:\cdots :s_n = 1^2:2^2:3^2:\cdots :n^2$

第一个$T$内、第二个$T$内、$\cdots$、第$n$个$T$内的位移之比：$s_1:s_2\cdots :s_n = 1:3:\cdots :(2n-1)$

连续相等的位移所用时间之比：$t_1:t_2:t_3:\cdots :t_n = 1:(\sqrt{2}-\sqrt{1}):(\sqrt{3}-\sqrt{2}):\cdots :(\sqrt{n}-\sqrt{n-1})$\

自由落体运动

初速度：$v_0=0$；末速度：$v_t=gt$

下落高度：$h=\dfrac{1}{2}gt^2$

有用推论：$v_t^2=2gh$

竖直上抛运动

位移：$s=v_0t-\dfrac{1}{2}gt^2$

末速度：$v_t=v_0-gt$

有用推论：$v_t^2-v_0^2=-2gs$

上升最大高度：$h=\dfrac{v_0^2}{2g}$

往返时间：$t=\dfrac{2v_0}{g}$

全过程处理：是匀速直线运动，以向上为正方向，加速度取负值；
分段处理：向上为匀减速直线运动，向下为自由落体运动，具有对称性；
上升与下落过程具有对称性，如在同点速度等值反向等。