动量冲量计算题训练
激光由于其单色性好、亮度高、方向性好等特点,在科技前沿的许多领域有着广泛的应用。根据光的波粒二象性可知,当光与其他物体发生相互作用时,光子表现出有能量和动量,对于波长为λ的光子,其动量$p=\dfrac{h}{\lambda}$。已知光在真空中的传播速度为$c$,普朗克常量为$h$。
(1)科研人员曾用强激光做过一个有趣的实验:一个水平放置的小玻璃片被一束强激光托在空中。已知激光竖直向上照射到质量为m的小玻璃片上后,全部被小玻璃片吸收,重力加速度为g。求激光照射到小玻璃片上的功率P;
(2)激光冷却和原子捕获技术在科学上意义重大,特别是对生物科学将产生重大影响。所谓激光冷却就是在激光的作用下使得做热运动的原子减速,其具体过程如下:一质量为m的原子沿着x轴负方向运动,频率为$v_0$的激光束迎面射向该原子。运动着的原子就会吸收迎面而来的光子从基态跃迁,而处于激发态的原子会立即自发地辐射光子回到基态。原子自发辐射的光子方向是随机的,在上述过程中原子的速率已经很小,因而光子向各方向辐射光子的可能性可认为是均等的,因而辐射不再对原子产生合外力的作用效果,并且原子的质量没有变化。
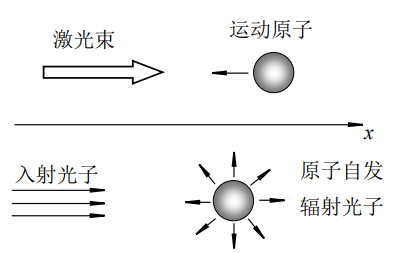
- ①设原子单位时间内与$n$个光子发生相互作用,求运动原子做减速运动的加速度$a$的大小;
- ②假设某原子以速度$v_0$沿着x轴负方向运动,当该原子发生共振吸收后跃迁到了第一激发态,吸收一个光子后原子的速度大小发生变化,方向未变。求该原子的第一激发态和基态的能级差ΔE?
展开答案
【答案】(1)$p=mgc$ ;(2) ①$a=\dfrac{nhv_0}{cm}$;②$\Delta E =hv_0(1+\dfrac{v_0}{c})-\dfrac{h^2v_0^2}{2c^2m}$
【详解】
(1)设在∆t时间内照射到玻璃表面的光子数为n,则由动量定理
$F\Delta t=np$
对玻璃板由平衡知识
$F=mg$
每个光子的能量
$E=hv=\dfrac{hc}{\lambda}=cp$
激光照射到小玻璃片上的功率
$P=\dfrac{nE}{\Delta t}$
解得
$P=mgc$
(2)①原子单位时间内与n个光子发生相互作用,由动量守恒定律
$n\dfrac{hv_0}{c}=m\Delta v$
原子的加速度
$a=\dfrac{\Delta v}{\Delta t}$
其中∆t=1s解得
$a=\dfrac{nhv_0}{cm}$
②以原子开始运动的方向为正方向,原子吸收一个光子的过程,由动量守恒定律
$mv_0-\dfrac{hv_0}{c}=mv$
该原子的第一激发态和基态的能级差
$\Delta = \dfrac{1}{2}mv_0^2+hv_0-\dfrac{1}{2}mv^2$
解得
$\Delta E = hv_0(1+\dfrac{v_0}{c})-\dfrac{h^2v_0^2}{2c^2m}$
质量为M=4kg的长木板A静止放在光滑水平地面上,质量为m1=4kg的小物块B位于木板A的左端,质量为m2=4kg的物块C位于木板A的右端,物块B与木板A间的动摩擦因数为μ=0.5,C物块下表面光滑。某时刻,使物块B以速度v1=2m/s的速度从左到右运动,同时使物块C以速度v2=2m/s从右向左运动,已知当A、B速度相等时,B、C发生碰撞,碰后粘在一起运动,重力加速度g取10m/s2,B、C均看为质点,则:
(1)木板A的最大速度为多少?
(2)A、B间摩擦产生的热量为多少?
展开答案
【解析】
(1)B、C碰撞前,A做加速运动,B、C碰撞后,A做减速运动,故A、B速度相等时,A的速度最大;
对A、B系统,取向右为正方向,由动量守恒定律:$m_1v_1=(m_1+M)v$
解得$v=1m/s$
(2)B、C碰撞过程,取向右为正方向,由动量守恒定律得:$m_1v-m_2v_2=(m_1+m_2)v′$
解得:$v′=-0.5m/s$
碰撞过程中能量损失为:$\Delta E_1=\dfrac{1}{2}m_1v^2+\dfrac{1}{2}m_2v_2^2-\dfrac{1}{2}(m_1+m_2)v′^2$
解得:$\Delta E_1$=9J
当A、B、C相对静止时有:$m_1v_1-m_2v_2=(M+m_1+m_2)v″$
解得:$v″=0$
A、B间摩擦产生的热量:$Q=\dfrac{1}{2}m_1v_2^2+\dfrac{1}{2}m_2v_2^2-\Delta E_1$
解得:Q=7J。
如图所示,一质量为0.5kg的一块橡皮泥自距小车上表面1.25m高处由静止下落,恰好落入质量为2kg、速度为2.5m/s沿光滑水平地面运动的小车上,并与小车一起沿水平地面运动,取g=10m/s2,不计空气阻力,下列说法正确的是
A.橡皮泥下落的时间为0.3s
B.橡皮泥与小车一起在水平地面上运动的速度大小为3.5m/s
C.橡皮泥落入小车的过程中,橡皮泥与小车组成的系统动量守恒
D.整个过程中,橡皮泥与小车组成的系统损失的机械能为7.5J
展开答案
【答案】D
【解析】橡皮泥下落的时间为:$t=\sqrt{dfrac{2h}{g}}=\sqrt{\dfrac{2\times1.25}{10}}=0.5s$.故A错误;橡皮泥与小车在水平方向的动量守恒,选取向右为正方向,则有:m1v0=(m1+m2)v,所以共同速度为:$v=\dfrac{m_1v_0}{m_1+m_2}=\dfrac{2\times2.5}{2+0.5}=2m/s$,故B正确;橡皮泥落入小车的过程中,橡皮泥与小车组成的系统在水平方向的动量守恒,但竖直方向的动量不守恒.故C错误;在整个的过程中,系统损失的机械能等于橡皮泥的重力势能与二者损失的动能,得:$\Delta=m_2gh+\dfrac{1}{2}m_1v_0^2-\dfrac{1}{2}(m_1+m_2)v^2$,代入数据可得:△E=7.5J.故D正确.
