动量冲量经典例题
(多选)关于动量的变化,下列说法中正确的是 ( )
A.做直线运动的物体速度增大时,动量的增量$Delta p$的方向与运动方向相同
B.做直线运动的物体速度减小时,动量的增量$Delta p$的方向与运动方向相反
C.物体的速度大小不变时,动量的增量$Delta p$为零
D.物体做平抛运动时,动量的增量一定不为零
展开答案
【答案】ABD
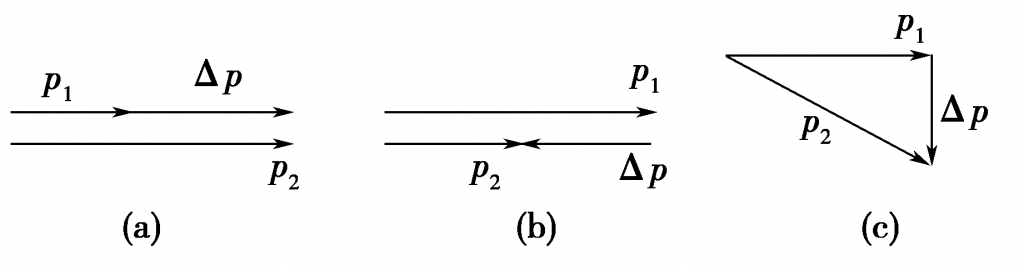
【解析】当做直线运动的物体的速度增大时,其末态动量$p_2$大于初态动量$p_1$,由矢量的运算法则可知$Delta p =p_2-p_1>0$,与物体运动方向相同,如图(a)所示,所以A选项正确。当做直线运动的物体速度减小时,$p_2<p_1$,如图(b)所示,$Delta p$与$p_1$(或$p_2$)方向相反,与运动方向相反,故B选项正确。当物体的速度大小不变时,其方向可能变化,也可能不变化,故动量可能不变化即Δp=0,也可能动量大小不变而方向变化,此种情况$Delta p≠0$,故C选项错误。当物体做平抛运动时,速度的大小和方向变化,即动量一定变化,$Delta p$一定不为零,如图(c)所示,故D选项正确。
一质量为m 的物体静止在光滑水平面上,在水平力F 作用下,经时间t,通过位移L后,动量变为p,动能变为Ek。若上述过程F 不变,物体的质量变为$dfrac{m}{2}$,以下说法正确的是( )
A.经过时间2t,物体动量变为2p
B.经过位移2L,物体动量变为2p
C.经过时间2t,物体动能变为4Ek
D.经过位移2L,物体动能变为4Ek
展开答案
【答案】A
【答案】A
【解析】由动量定理得$p=Ft$,则经过时间2t,物体的动量$p_2=F·2t=2p$,由$p^2=2mE_k$得物体的动能$E_{k2}=dfrac{2p^2}{2dfrac{m}{2}}=8E_K$,选项A正确,C错误;
由动能定理$E_k=FL$,则经过位移$2L$,物体的动能$E_{k2}=F2L=2E_k$,由$p^2=2mE_k$,得物体的动量$P_2=sqrt{2 dfrac{m}{2}2E_k}=p$,选项B、D错误。
若采用下图中甲、乙两种实验装置来验证动量守恒定律(图中小球半径相同、质量均已知,且mA>mB,B、B´两点在同一水平线上),下列说法正确的是
A.采用图甲所示的装置,必需测量OB、OM、OP和ON的距离
B.采用图乙所示的装置,必需测量OB、B´N、B´P和B´M的距离
C.采用图甲所示的装置,若$m_Acdot ON=m_A cdot OP +m_B cdot OM$,则表明此碰撞动量守恒
D.采用图乙所示的装置,若$dfrac{1}{sqrt{B’N}}=dfrac{1}{sqrt{B’M}}+dfrac{1}{sqrt{B’P}}$,则表明此碰撞机械能也守恒
展开答案
【答案】D
【解析】A. 如果采用图甲所示装置,由于小球平抛运动的时间相等,故可以用水平位移代替速度进行验证,不需要测量OB的长度,故A错误;
B. 如果采用图乙所示装置时,利用水平距离相等,根据下落的高度可确定飞行时间,从而根据高度可以表示出对应的水平速度,从而确定动量是否守恒,故不需要测量OB的距离,故B错误;
C. 采用图甲所示装置,一个球时水平距离为OP,两球相碰时,A球距离为OM,B球为ON,则根据动量守恒定律有:$m_Av=m_Av_1+m_B+m_Bv_2$,因下落时间相同,则两端同时乘以t后有$m_Acdot OP=m_A cdot OM +m_B cdot ON$,则表明此碰撞动量守恒,故C错误;
D. 小球碰后做平抛运动,速度越快,下落高度越小,单独一个球下落时,落点为P,两球相碰后,落点分别为M和N,根据动量守恒定律有$m_Av=m_Av_1+m_bv_2$,而速度$v=dfrac{l}{t}$,根据$h=dfrac{1}{2}gt^2$可得$t=dfrac{2h}{g}$,则可解得:
$v=dfrac{BB’}{sqrt{dfrac{2B’P}{g}}}$
$v_1=dfrac{BB’}{sqrt{dfrac{2B’M}{g}}}$
$v_2=dfrac{BB’}{sqrt{dfrac{2B’N}{g}}}$
代入动量守恒表达式,消去公共项后,有$dfrac{m_A}{sqrt{B’P}}=dfrac{m_A}{sqrt{B’M}}+dfrac{m_A}{sqrt{B’N}}$,机械能守恒定律可知:$dfrac{1}{2}m_Av^2=dfrac{1}{2}m_Av_1^2+dfrac{1}{2}m_Bv_2^2$,联立动量表达式和机械能表达式可知:$dfrac{1}{sqrt{B’N}}=dfrac{1}{sqrt{B’M}}+dfrac{1}{sqrt{B’P}}$,故可以根据该式表明此碰撞机械能守恒,故D正确;
故选D.
如图所示,一质量为0.5kg的一块橡皮泥自距小车上表面1.25m高处由静止下落,恰好落入质量为2kg、速度为2.5m/s沿光滑水平地面运动的小车上,并与小车一起沿水平地面运动,取g=10m/s2,不计空气阻力,下列说法正确的是
A.橡皮泥下落的时间为0.3s
B.橡皮泥与小车一起在水平地面上运动的速度大小为3.5m/s
C.橡皮泥落入小车的过程中,橡皮泥与小车组成的系统动量守恒
D.整个过程中,橡皮泥与小车组成的系统损失的机械能为7.5J
展开答案
【答案】D
【解析】橡皮泥下落的时间为:$t=sqrt{dfrac{2h}{g}}=sqrt{dfrac{2times1.25}{10}}=0.5s$.故A错误;橡皮泥与小车在水平方向的动量守恒,选取向右为正方向,则有:m1v0=(m1+m2)v,所以共同速度为:$v=dfrac{m_1v_0}{m_1+m_2}=dfrac{2times2.5}{2+0.5}=2m/s$,故B正确;橡皮泥落入小车的过程中,橡皮泥与小车组成的系统在水平方向的动量守恒,但竖直方向的动量不守恒.故C错误;在整个的过程中,系统损失的机械能等于橡皮泥的重力势能与二者损失的动能,得:$Delta=m_2gh+dfrac{1}{2}m_1v_0^2-dfrac{1}{2}(m_1+m_2)v^2$,代入数据可得:△E=7.5J.故D正确.
如图所示,两平行光滑杆水平放置,两相同的小球M、N分别套在两杆上,并由轻弹簧拴接,弹簧与杆垂直。已知两杆间距为0.4m,弹簧原长为0.5m,两球的质量均为0.2kg。现给M球一沿杆向右0.6N.S的瞬时冲量,关于之后的运动,以下说法正确的是( )
A.M球在开始的一段时间内做加速度增大的加速运动,直到达到运动中的最大速度
B.弹簧第一次达到0.6m时,M球的速度大小为3m/s
C.弹簧达到0.5m时,M球和N球总动能最大
D.弹簧达到最长时,M球的速度大小为1.5m/s
展开答案
【答案】BCD
【解析】A.在最开始时,弹簧处于压缩状态,当M球开始运动后,弹簧恢复原长,形变量逐渐减小,因此弹力逐渐减小,根据牛顿第二定律可知,加速度逐渐减小,即该过程M球做加速度逐渐减小的加速运动,故A错误;
B.设一开始弹簧的形变量为$x_1$,当弹簧达到0.6m时形变量为$x_2$,则有
$x_1=0.5-0.4=0.1m$
$x_2=0.6-0.5=0.1m$
M球在瞬间冲量作用后,获得动量,由动量定理可得
$I_M=0.6Ncdot s= m_MV_0$
两球和弹簧组成的系统,合外力为零,根据动量守恒定律可得
$m_MV_0=m_MV_1+m_N+v_2$
当弹簧第一次达到0.6m时,根据能量守恒定律有
$dfrac{1}{2}k_1^2+dfrac{1}{2}m_MV_0^2=dfrac{1}{2}m_MV_1^2+dfrac{1}{2}m_NV_2^2+dfrac{1}{2}kx_2^2$
解得
$V_1=3m/s$
即弹簧达到0.6m时,M球的速度大小为3m/s,故B正确;
C.根据能量守恒定律,该过程M球和N球的总动能与弹簧的弹性势能相互转化,当弹簧的弹性势能为0时,M球和N球的总动能达到最大。故C正确。
D.当两球速度第一次相等时,弹簧第一次达到最大伸长量,根据动量守恒定律可得
$m_MV_0=(m_M+m_N)V_g$
解得
$V_g=1.5m/s$
即弹簧达到最长时,M球的速度大小为1.5m/s,故D正确。
2022年10月1日,中国女篮在女篮世界杯决赛中获得亚军,追平了在本项赛事中的历史最好成绩。如图所示,水平地面上,某运动员手拿篮球站在滑板车上向一堵竖直的墙(向右)滑行,为了避免与墙相撞,在接近墙时,运动员将篮球水平向右抛出,篮球反弹后运动员又接住篮球,速度恰好减为0。不计地面的摩擦和空气阻力,忽略篮球在竖直方向的运动,篮球与墙的碰撞过程不损失能量。运动员和滑板车的总质量为M,篮球的质量为m。抛球前,运动员、滑板车和篮球的速度为$v_0$。则( )
A.整个过程中运动员、滑板车及篮球的总动量守恒
B.运动员抛球与接球时对篮球的冲量相同
C.墙对篮球的冲量大小为$dfrac{1}{2}(M+m)v_0$
D.篮球被墙反弹后的速度大小为$dfrac{M+m}{2m}v_0$

展开答案
【答案】D
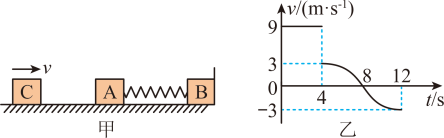
如图甲所示,物块A、B的质量分别为2kg、3kg,用轻弹簧拴接,放在光滑的水平地面上,物块B右侧与竖直墙壁接触但不黏连。物块 C 从 t=0时以一定速度向右运动,在t=4s时与物块A相碰,并立即与物块A粘在一起不再分开,物块 C 的v-t 图像如图乙所示,下列说法正确的是
A.物块C的质量为2kg
B.物块B离开墙壁前,弹簧的最大弹性势能为40.5J
C.4s到12s的时间内,弹簧对物块A的冲量大小为12N.s
D.物块B离开墙壁后的最大速度为3m/s
展开答案
【答案】D
【解析】

如图所示,竖直平面内有一半圆槽,A、C等高,B为圆槽最低点,小球从A点正上方O点静止释放,从A点切入圆槽,刚好能运动至C点.设球在AB段和BC段运动过程中,运动时间分别为t 1 、t 2 ,合外力的冲量大小为I 1 、I 2 ,则( )
A. t 1 >t 2 B. t 1 =t 2 C. I 1 >I 2 D. I 1 =I 2
展开答案
【答案】C
【解析】小球从A点正上方O点静止释放,做自由落体运动,从A点切入圆槽,刚好能运动至C点.即从A到C速度越来越小,AB段平均速率大于BC段平均速率,两段路程相等,所以球在AB段和BC段运动过程中的运动时间为t1<t2,AB不符合题意;
沿圆心方向的合力与速度垂直,动量变化为零,AB段平均速率大于BC段平均速率,说明切线方向上AB段速度变化量较大,根据动量定理,合外力的冲量等于动量的变化,所以合外力的冲量大小为 I 1 >I 2
计算变力的冲量,一般用动量的变化来衡量!
(2014·全国·高考真题)一中子与一质量数为A(A>1)的原子核发生弹性正碰.若碰前原子核静止,则碰撞前与碰撞后中子的速率之比为( )
A.$dfrac{A+1}{A-1}$ B.$dfrac{A-1}{A+1}$ C.$dfrac{4A}{(A+1)^2}$ D.$dfrac{(A+1)^2}{(A-1^2)}$
展开答案
【解析】A
【解析】设中子的质量为m,因为发生的是弹性正碰,动量守恒,机械能守恒,规定初速度的方向为正方向,有:$mv_1=mv_2+Amv$,$dfrac{1}{2}mv_1^2=dfrac{1}{2}mv_2^2+dfrac{1}{2}Amv^2$
联立两式解得:$dfrac{v_1}{v_2}=dfrac{A+1}{A-1}$.故A正确,BCD错误.故选A.
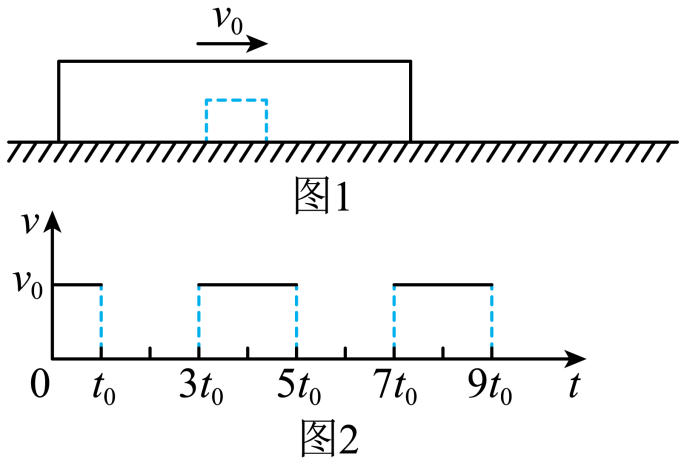
(2008·山东·高考真题).一个物体静置于光滑水平面上,外面扣一质量为M的盒子,如图1所示。现给盒子一初速度v0,此后,盒子运动的v–t图象呈周期性变化,如图2所示。请据此求盒内物体的质量。
展开答案
【答案】m=M
【解析】设物体的质量为m。t0时刻受盒子碰撞获得速度v,根据动量守恒定律
Mv0=mv①
3t0时刻物体与盒子右壁碰撞使盒子速度又变为v0,说明碰撞是弹性碰撞,能量守恒
$dfrac{1}{2}mv_0^2=dfrac{1}{2}mv^2$②
联立①②解得:m=M
(复旦大学自主招生)太空飞船在宇宙空间中飞行时,会遇到太空尘埃的碰撞而受到阻碍作用。设单位体积的太空均匀分布着尘埃 n 颗,每颗尘埃平均质量为 m ,尘埃速度可忽略、飞船的横截面积为 S ,与尘埃碰撞后将尘埃完全黏附住。当飞船维持恒定的速率 v 飞行时,飞船引擎需要提供的平均推力为( )
A.$dfrac{1}{2}nmv^2S$ B.$nmv^2S$ C.$dfrac{3}{2}nmv^2S$ D.$dfrac{1}{3}nmv^2S$
展开答案
【答案】B
【解析】以飞船为参照物,选择一和飞船横截面积相等的圆柱内的尘埃进行研究。
则该圆柱内的尘埃相对于飞船以速度v做匀速直线运动,在t时间内,由长度为x=vt,横截面积为S、体积为V=vtS的尘埃柱碰到飞船上,尘埃柱内尘埃颗粒数目为N=nvtS,尘埃总质量为M=Nm=mnvtS,根据动量定理,Ft=Mv,联立解得:F=nmv2S,选项B正确。
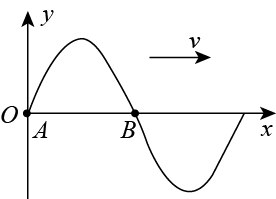
(2011·天津·高考真题)(多选)位于坐标原点处的波源A沿y轴做简谐运动,A刚好完成一次全振动时,在介质中形成简谐横波的波形如图所示,B是沿波传播方向上介质的一个质点,则( )
A.波源A开始振动时的运动方向沿y轴负方向
B.此后的$dfrac{1}{4}$周期内回复力对波源A一直做负功
C.经半个周期时间质点B将向右迁移半个波长
D.在一个周期时间内A所受回复力的冲量为零
展开答案
答案:ABD
