带电粒子在磁场中的运动知识点

---

1．洛伦兹力的定义

磁场对运动电荷的作用力

2．洛伦兹力的大小

(1)v∥B时，F＝0；

(2)v⊥B时，F＝qvB；

(3)v与B的夹角为θ时，F＝qvBsin θ.

3．洛伦兹力的方向

---

---

---

1．临界条件

带电粒子刚好穿出(不穿出)磁场边界的条件是带电粒子在磁场中运动的轨迹与边界相切，故边界(边界的切线)与轨迹过切点的半径(直径)垂直．

2．解题步骤

分析情景→作基础图→作动态图→确定临界轨迹→分析临界状态→构建三角形→解三角形

3．常见的几种临界情况

(1)直线边界

最长时间：弧长最长，一般为轨迹与直线边界相切．

最短时间：弧长最短(弦长最短)，入射点确定，入射点和出射点连线与边界垂直．

如图1，P为入射点，M为出射点．

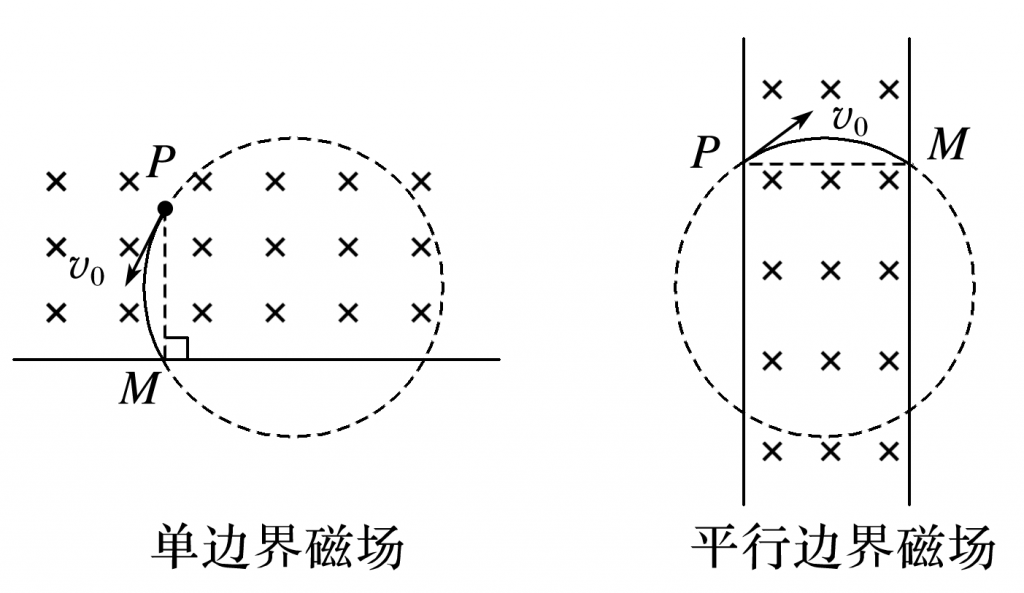
(2)圆形边界：公共弦为小圆直径时，出现极值，即：

当运动轨迹圆半径大于圆形磁场半径时，以磁场直径的两端点为入射点和出射点的轨迹对应的圆心角最大．

模型一　“平移圆”模型

模型二　“旋转圆”模型

模型三　“放缩圆”模型

模型四　“磁聚焦”模型

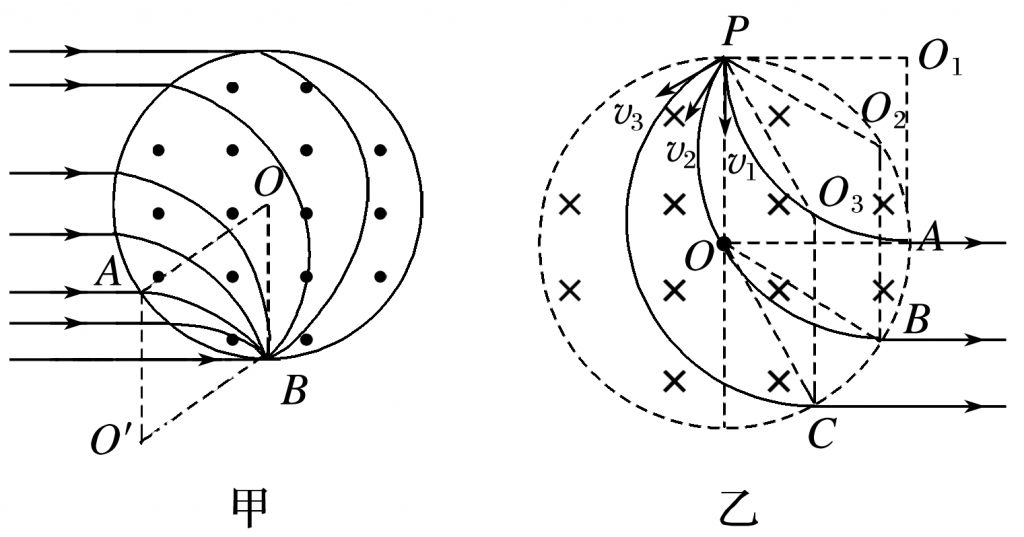
1．带电粒子的会聚

如图甲所示，大量的同种带正电的粒子，速度大小相同，平行入射到圆形磁场区域，如果轨迹圆半径与磁场圆半径相等(R＝r)，则所有的带电粒子将从磁场圆的最低点B点射出．(会聚)

证明：四边形OAO′B为菱形，必是平行四边形，对边平行，OB必平行于AO′(即竖直方向)，可知从A点发出的带电粒子必然经过B点．

2．带电粒子的发散

如图乙所示，有界圆形磁场的磁感应强度为B，圆心为O，从P点有大量质量为m、电荷量为q的正粒子，以大小相等的速度v沿不同方向射入有界磁场，不计粒子的重力，如果正粒子轨迹圆半径与有界圆形磁场半径相等，则所有粒子射出磁场的方向平行．(发散)

证明：所有粒子运动轨迹的圆心与有界圆圆心O、入射点、出射点的连线为菱形，也是平行四边形，O₁A(O₂B、O₃C)均平行于PO，即出射速度方向相同(即水平方向)．