近代物理初步
1.(多选)已知某金属发生光电效应的截止频率为νc,则( )
A.当用频率为2νc的单色光照射该金属时,一定能产生光电子
B.当用频率为2νc的单色光照射该金属时,所产生的光电子的最大初动能为hνc
C.当照射光的频率ν大于νc时,若ν增大,则逸出功增大
D.当照射光的频率ν大于νc时,若ν增大一倍,则光电子的最大初动能也增大一倍
展开答案
【答案】AB
【解析】该金属的截止频率为νc,则可知逸出功$W_0=hν_c$,逸出功由金属材料的性质决定,与照射光的频率无关,因此C错误;
由光电效应的实验规律可知A正确;由爱因斯坦光电效应方程$E_k=hν-W_0$,将$W0=hν_c$代入可知B正确,D错误。
如图所示,在研究光电效应实验的电路中,设光电管阴极K的逸出功为$W_0$,电源的电动势$E=4.0V$,内阻可忽略。滑动变阻器的金属丝电阻均匀,总有效长度为$L$。滑动触头$P$置于金属电阻丝的正中央$c$点,闭合开关,用光子能量为$3.5 eV$的一束单色光照射光电管阴极$K$,发现灵敏电流计示数不为零;将滑动触头$P$从$c$点向左移动$\dfrac{1}{4}L$,电流计示数刚好减小到零。若将滑动触头$P$从$c$点向右移动$\dfrac{1}{4}L$,光电子到达阳极A的最大动能为,则$E_{kmax}$( )
A.$W_0=2.5 eV,E_{kmax}=1.0 eV$
B.$W_0=2.5 eV,E_{kmax}=2.0 eV$
C.$W_0=1.0 eV,E_{kmax}=1.0 eV$
D.$W_0=1.0 eV,E_{kmax}=2.0 eV$
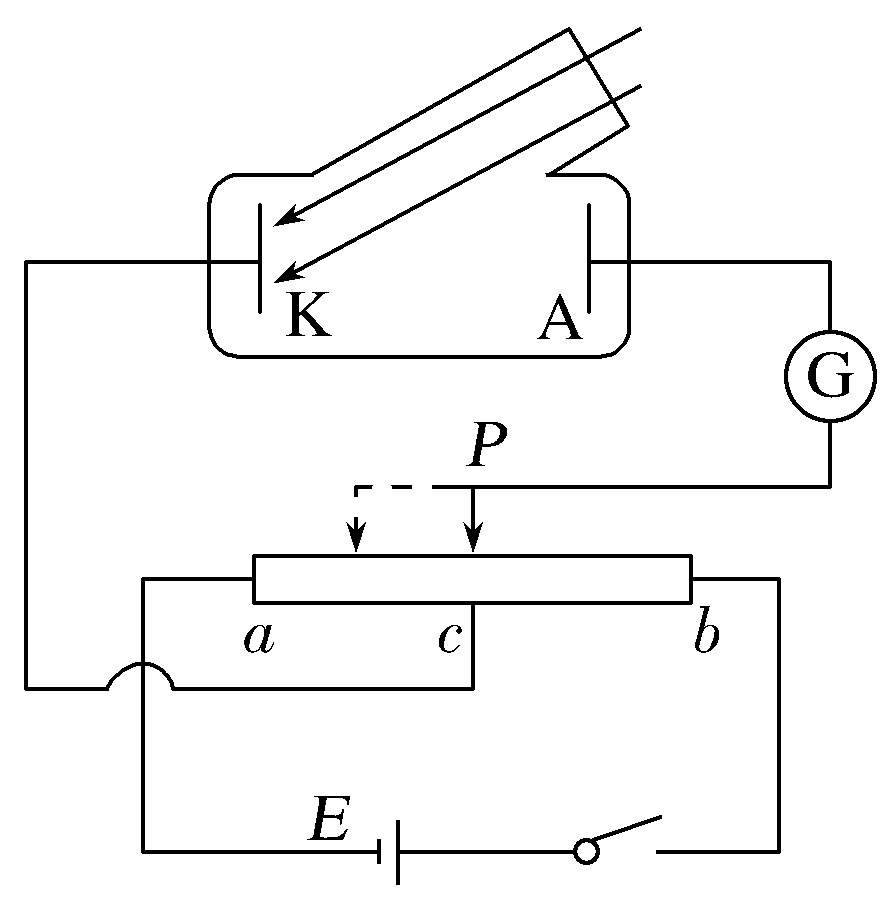
展开答案
【答案】A
【解析】 入射光的光子能量$ε=hν=3.5 eV$,阴极$K$的逸出功为$W_0$,则逸出光电子的最大初动能$E_{k1}=hν-W_0$;
$P$从$c$点向左移动$\dfrac{1}{4}L$,光电管上加有反向电压$U=\dfrac{1}{4}E=1.0 V$,电流计示数刚好减小到零,故$-eU=0-E_{k1}$,$E_{k1}=1.0 eV$,$W_0=3.5 eV-1.0 eV=2.5 eV$;
触头P从c点向右移动$\dfrac{1}{4}L$时,光电管上加有正向电压$U=\dfrac{1}{4}E=1.0eV$,则光电子到达阳极A的最大动能$E_{kmax}=E_{k1}+eU′=2.0 eV$,故选项B正确。
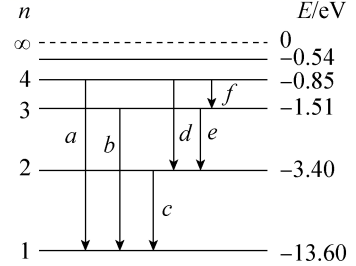
氢原子的能级图如图甲所示,一群处于第4能级的氢原子,向低能级跃迁过程中能发出几种不同频率的光,其中只有频率为$v_1$、$v_2$的两种光可让图乙所示的光电管阴极K发生光电效应,现分别用频率为$v_1$或$v_2$的三个光源a、b、c分别照射该光电管阴极K,测得电流随电压变化的图像如图丙所示,下列说法中正确的是
A.一群处于第4能级的氢原子向低能级跃迁时最多能发出4种不同频率的光子
B.图线c对应的光是氢原子由第3能级向第1能级跃迁发出的
C.图线a对应的光子频率大于图线c对应的光子频率
D.用图线6对应的光照射光电管时,光电流会随着正向电压的增大而不断增大
展开答案
【答案】 B
【解析】 一群4-1 就是$C_4^2=6$,一个是$n-1=4-1=3$。所以A错
根据图像,只有两种能发生光电效应,那么肯定是跨越能级最高的两个!分别是4-1和3-1 ,由$eU_C=hv-w_0$,可以推断b的4-1,那么b、c都是3-1,所以B对
(2021·浙江湖州、衢州、丽水质检)下列说法正确的是( )
A.光电效应说明光具有粒子性,康普顿效应说明光具有波动性
B.天然放射的三种射线,电离能力最弱的是α射线
C.电子束穿过铝箔后的衍射图样说明电子具有波动性
D.卢瑟福α粒子散射实验,揭示了原子只能处于一系列不连续的能量状态中
展开答案
【答案】 C
【解析】
在原子物理学中,康普顿散射,或称康普顿效应(英语:Compton effect),是指当X射线或伽马射线的光子跟物质相互作用,因失去能量而导致波长变长的现象。相应的还存在逆康普顿效应——光子获得能量引起波长变短。这一波长变化的幅度被称为康普顿偏移。
康普顿效应首先在1923年由美国华盛顿大学物理学家康普顿观察到,并在随后的几年间由他的研究生吴有训进一步证实。康普顿因发现此效应而获得1927年的诺贝尔物理学奖。
这个效应反映出光不仅仅具有波动性。此前汤姆孙散射的经典波动理论并不能解释此处波长偏移的成因,必须引入光的粒子性。这一实验说服了当时很多物理学家相信,光在某种情况下表现出粒子性,光束类似一串粒子流,而该粒子流的能量与光频率成正比。
在引入光子概念之后,康普顿散射可以得到如下解释:电子与光子发生弹性碰撞(弹性碰撞产生的非弹性散射),电子获得光子的一部分能量而反弹,失去部分能量的光子则从另一方向飞出,整个过程中总动量守恒,如果光子的剩余能量足够多的话,还会发生第二次甚至第三次弹性碰撞。
康普顿散射可以在任何物质中发生。当光子从光子源发出,射入散射物质(一般指金属)时,主要是与电子发生作用。如果光子的能量相当低(与电子束缚能同数量级),则主要产生光电效应,原子吸收光子而产生电离。如果光子的能量相当大(远超过电子的束缚能)时,则我们可以认为光子对自由电子发生散射,而产生康普顿效应。如果光子能量极其大(>1.022百万电子伏特)则足以轰击原子核而生成一对粒子:电子和正电子,这个现象被称为成对产生。
由于光子具有波粒二象性,因此,应该可以用波动理论诠释这效应。埃尔温·薛定谔于1927年给出半经典理论。这理论是用经典电动力学来描述光子,用量子力学来描述电子。
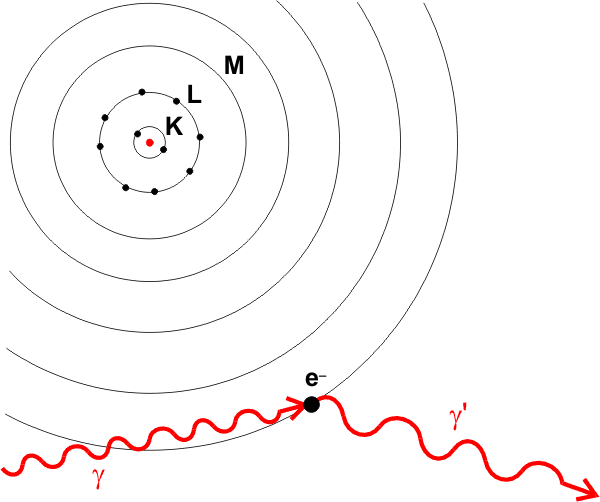
康普顿效应
光电效应、康普顿效应均说明光具有粒子性,故A错误;
天然放射的三种射线,电离能力最弱的是γ射线,α射线电离能力最强,故B错误;
电子束穿过铝箔后的衍射图样说明电子能发生衍射,具有波动性,故C正确;
卢瑟福α粒子散射实验,揭示了在原子内部存在原子核,故D错误。
关于核反应方程$^{238}_{92}U \rightarrow ^x_{90}Th+^4_2He$,其中$x$为$Th$原子核的质量数,则下列说法正确的是( )
A.该反应属于$\beta$衰变
B.$ ^x_{90}Th$中含有144个中子
C.$^{238}_{92}U$的平均结合能比$ ^x_{90}Th$大
D.该反应新生成的粒子$ ^x_{90}Th$不具有放射性
展开答案
【答案】 B
【解析】
A.该反应属于$\alpha$衰变,故A错误。
B.$ ^x_{90}Th$的质量数为238-4=234(个)。
$ ^x_{90}Th$中含有的中子数为234-90=144(个)故B正确。
C.$^{238}_{92}U$衰变过程中释放能量,新核更稳定,因此新核$ ^x_{90}Th$的比结合能较大,故C错误。
D.$ ^x_{90}Th$具有放射性,它能放出一个电子而衰变成镤核,故D错误。
氡222检测是指使用采样泵或自由扩散方法将待测空气中的氡抽入或扩散进入测量室,通过直接测量所收集氡产生的子体产物或经静电吸附浓集后的子体产物的a放射性,推算出待测空气中氡的浓度的测量过程。已知质量为m0的氡222,经过时间t后剩余的氡222质量为m,其$\dfrac{m}{m_0}-t$图像如图所示。从图中可以得到氡222的半衰期为( )
A.1.22d B.3.91d C.5.02d D.3.80d
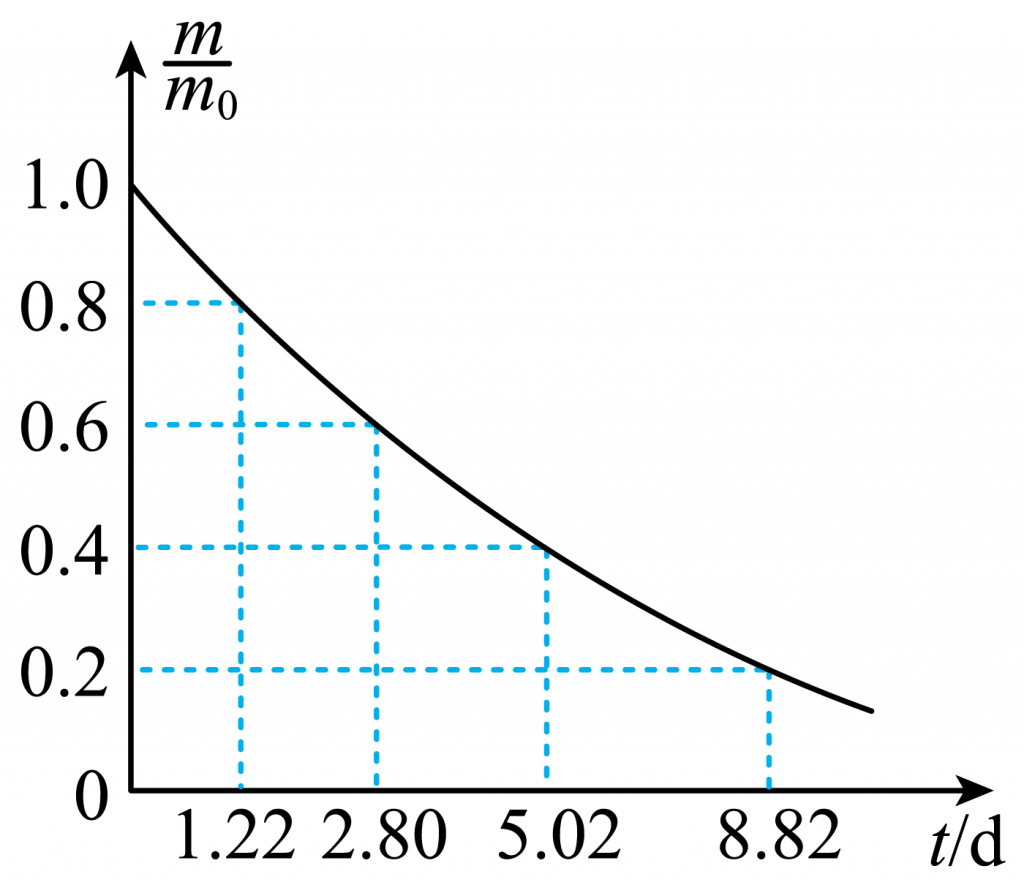
展开答案
【答案】 D
【解析】
由图可知质量为0.8m0的氡222变到0.4m0所用的时间
$\Delta t =3.80d$
0.4m0的氡222衰变到0.2m0所用的时间
$\Delta t ‘=3.80d$
即氡222的半衰期为3.80d。故ABC错误,D正确。
一群处于基态的氢原子吸收某种单色光子后,向外辐射了$v_1$,$v_2$,$v_3$三种频率的光子,且$v_3>v_2>v_1$,则
A.$v_2:v_3=27:32$
B.被氢原子吸收的光子能量为$h(v_1+v_2+v_3)$
C.用光子能量为$h(v_1+v_2)$的单色光照射处于基态的原子,可以使氢原子电离。
D.$v_1$,$v_2$,$v_3$三种频率的光子对应的波长分别为$\lambda_1$、$\lambda_2$、$\lambda_2$、则有$\lambda_1=\lambda_2+\lambda_3$
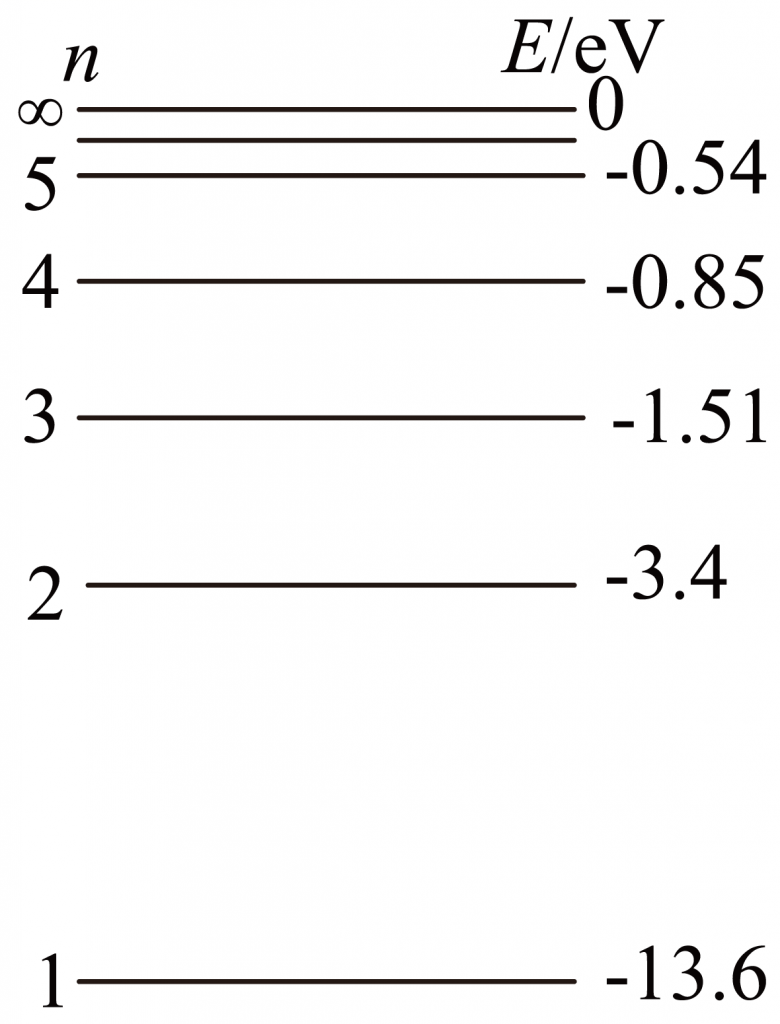
展开答案
【答案】 A
【解析】根据玻尔理论,处于基态的氢原子被12.75eⅤ光子照射,可跃迁至第四能级,自第四能级向下跃迁可释放6种不同频率的光子,如图所示,c光子能量
Ec=-3.4eV-(-13.6eV)=10.2eV
为紫外线,a、b光子能量大于c光子能量,也为紫外线
Ed=0.85eV-(-3.4eV)=2.55cV
为可见光,e光子能量
Ee=-1.51eV-(-3.4eV)=1.89eV
为可见光
Ef=-0.85eV-(-1.51eV)=0.66eV<1.62eV
为不可见光;
因此有3种紫外线,2种可见光,1种不可见光,A正确。
智能手机带有感光功能,可以自动调整屏幕亮度,其光线传感器的工作原理是光电效应。在光电效应中,当一定频率的光照射某种金属时,实验得到的遏止电压$U_c$与入射光的频率v的关系如图所示,其横截距为$a$,纵截距为$-b$,元电荷电量为。下列说法正确的是( )
A.遏止电压与入射光的频率成正比
B.金属的截止频率为$b$
C.金属的逸出功为$eb$
D.普朗克常量$h=\dfrac{ea}{b}$
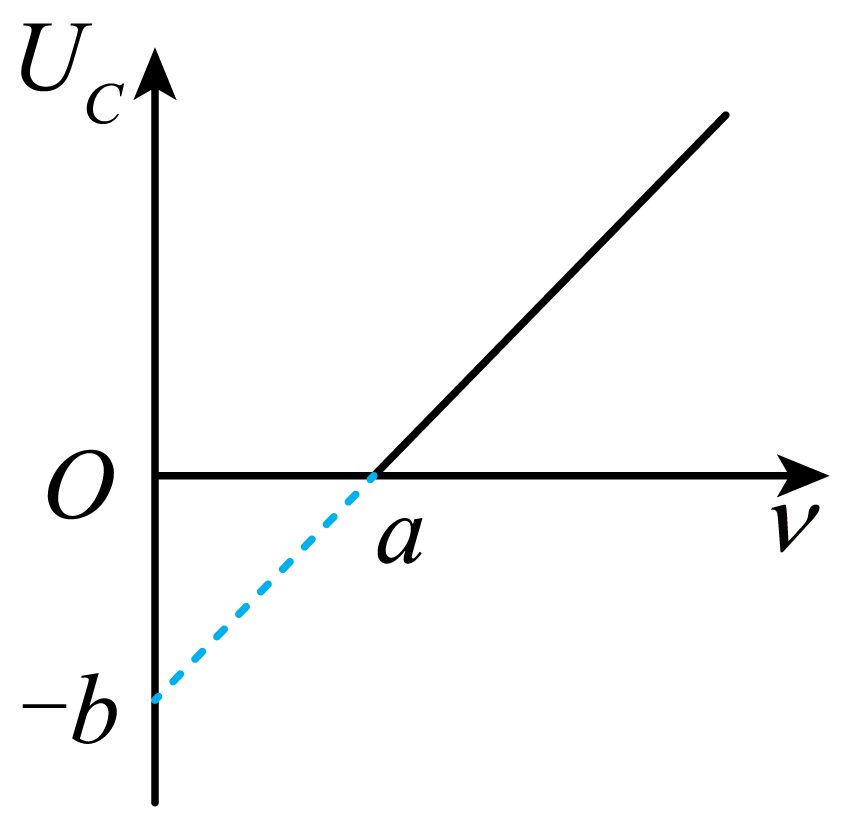
展开答案
【答案】 C
【解析】
A.由$eU_C=E_{km}=hv-W_0$得$U_C=\dfrac{h}{e}v-\dfrac{W_0}{e}$
入射光的频率与遏止电压成线性关系但不是正比关系,故A错误;
B.由公式$W_0= h v_0$
得金属的截止频率
$v_0=\alpha$
故B错误;
CD.结合图像得
$k=\dfrac{h}{e}=\dfrac{b}{a}$,$\dfrac{W_0}{e}=b$
故金属的逸出功$W_0=eb$,普朗克常量$h=\dfrac{eb}{a}$,故C正确,D错误。
氢原子的能级如图所示,已知可见光的光子能量范围约为$1.62eV-3.11eV$,下列说法正确的是( )
A.处于$n=3$能级的氢原子可以吸收任意频率的紫外线,并发生电离
B.大量氢原子从高能级向$n=3$能级跃迁时,发出的光是紫外线
C.大量处于$n=4$能级的氢原子向低能级跃迁时,可能发出2种不同频率的可见光
D.大量处于$n=4$能级的氢原子向基态跃迁时所发出的光子通过同一双缝干涉实验装置,以$n=4$直接跃迁到$n=1$能级发出的光子所形成的干涉条纹最宽

展开答案
【答案】 AC
【解析】
A.由于紫外线的能量大于$3.11eV$,并且也大于处于$n=3$能级的能量$-1.51eV$,则紫外线能让处于$n=3$能级的氢原子发生电离,所以A正确;
B.量氢原子从高能级向$n=3$能级跃迁时,发出的光其能量小于$-1.51eV$,所以是红外线,则B错误;
C.大量处于$n=4$能级的氢原子向低能级跃迁时,可能发出6种不同频率的光,如
$4\rightarrow3$ ,$\Delta E_1=E_4-E_3=0.66eV$
$4\rightarrow2$ ,$\Delta E_2=E_4-E_2=2.55eV$
$4\rightarrow1$ ,$\Delta E_3=E_4-E_1=12.75eV$
$3\rightarrow2$ ,$\Delta E_4=E_3-E_2=1.89eV$
$3\rightarrow1$ ,$\Delta E_5=E_3-E_1=12.09eV$
$2\rightarrow1$ ,$\Delta E_6=E_2-E_1=10.02eV$
由于可见光的光子能量范围约为$1.62eV-3.11eV$,则大量处于$n=4$能级的氢原子向低能级跃迁时,可能发出2种不同频率的可见光,所以C正确;
D.$n=4$直接跃迁到$n=1$能级发出的光子能量最大,则其波长最短,根据
$\Delta=\dfrac{L}{d}\lambda$
则大量处于$n=4$能级的氢原子向基态跃迁时所发出的光子通过同一双缝干涉实验装置,以$n=4$直接跃迁到$n=1$能级发出的光子所形成的干涉条纹最窄,所以D错误;
(2021·北京·高考真题)北京高能光源是我国首个第四代同步辐射光源,计划于2025年建成。同步辐射光具有光谱范围宽(从远红外到X光波段,波长范围约为10-5m~10-11m,对应能量范围约为10-1eV~105eV)、光源亮度高、偏振性好等诸多特点,在基础科学研究、应用科学和工艺学等领域已得到广泛应用。速度接近光速的电子在磁场中偏转时,会沿圆弧轨道切线发出电磁辐射,这个现象最初是在同步加速器上观察到的,称为“同步辐射”。以接近光速运动的单个电子能量约为109eV,回旋一圈辐射的总能量约为104eV。下列说法正确的是( )
A.同步辐射的机理与氢原子发光的机理一样
B.用同步辐射光照射氢原子,不能使氢原子电离
C.蛋白质分子的线度约为10-8 m,不能用同步辐射光得到其衍射图样
D.尽管向外辐射能量,但电子回旋一圈后能量不会明显减小
展开答案
【答案】D
【解析】A.同步辐射是在磁场中圆周自发辐射光能的过程,氢原子发光是先吸收能量到高能级,在回到基态时辐射光,两者的机理不同,故A错误;
B.用同步辐射光照射氢原子,总能量约为104eV大于电离能13.6eV,则氢原子可以电离,故B错误;
C.同步辐射光的波长范围约为10-5m~10-11m,与蛋白质分子的线度约为10-8 m差不多,故能发生明显的衍射,故C错误;
D.以接近光速运动的单个电子能量约为109eV,回旋一圈辐射的总能量约为104eV,则电子回旋一圈后能量不会明显减小,故D正确;
2021·全国·高考真题)如图,一个原子核X经图中所示的一系列$\alpha$、$\beta$衰变后,生成稳定的原子核Y,在此过程中放射出电子的总个数为( )
A.6
B.8
C.10
D.14
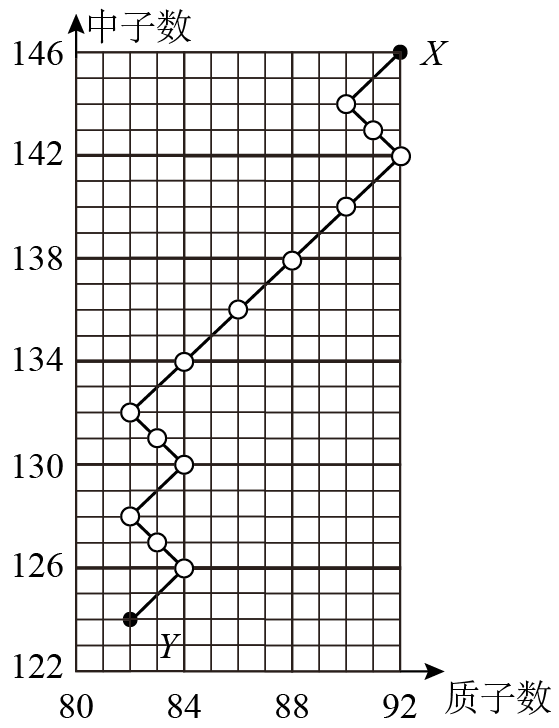
展开答案
【答案】A
【解析】由图分析可知,核反应方程为
$^{238}_{92}X \rightarrow ^{206}_{82}Y+a^{4}_{2}He+b^{0}_{-1}e$
设经过a次$\alpha$衰变,b次$\beta$衰变。由电荷数与质量数守恒可得
$238=206+4a$;$92=82+2a-b$
解得
$a=8,b=6$
故放出6个电子。
(2020·全国·高考真题)氘核$^2_1H$可通过一系列聚变反应释放能量,其总效果可用反应式$6^2_1H \rightarrow 2^4_2H+2^1_1H+2^1_0n+43.15MeV$表示。海水中富含氘,已知$1kg$海水中含有的氘核约为$1.0×10^22$个,若全都发生聚变反应,其释放的能量与质量为M的标准煤燃烧时释放的热量相等;已知1 kg标准煤燃烧释放的热量约为$2.9×10^7 J$,$1 MeV= 1.6×10^{–13}J$,则$M$约为( )
A.$40kg$ B.$100kg$ C.$400 kg $ D.$1000 kg$
展开答案
【答案】C
【解析】氘核$^2_1$可通过一系列聚变反应释放能量,其总效果可用反应式
$6^2_1H \rightarrow 2^4_2H+2^1_1H+2^1_0n+43.15MeV$
则平均每个氘核聚变释放的能量为
$\varepsilon = \dfrac{E}{6}=\dfrac{43.15}{6}MeV$
1kg海水中含有的氘核约为1.0×1022个,可以放出的总能量为
$E_0=N \varepsilon$
由$Q=mq$可得,要释放的相同的热量,需要燃烧标准煤燃烧的质量
$m=\dfrac{Q}{q}=\dfrac{E_0}{q}=400kg$
“微光夜视仪”是利用光电效应原理工作的一种仪器。被视物体反射的红外辐射照射在“银氧铯”阴极上激发出光电子,电子的电荷量大小为e,下列说法正确的是( )
A.红外辐射的频率可以很低,但辐射强度必须足够大才能发生光电效应
B.向右调节滑动变阻器的滑片,电流表的示数将随电压表示数的增大而增大
C.保持红外辐射强度不变,提高红外辐射的频率,则饱和电流值将减小
D.调换电源正负极,调节滑动变阻器,电压表示数为U时,电流表示数恰为零,则光电子逸出金属表面时的初动能为Ue
展开答案
答案 C
