牛顿运动定律的应用及计算题
(全国卷Ⅲ)如图,两个滑块A和B的质量分别为mA=1 kg和mB=5 kg,放在静止于水平地面上的木板的两端,两者与木板间的动摩擦因数均为μ1=0.5;木板的质量为m=4 kg,与地面间的动摩擦因数为μ2=0.1.某时刻A、B两滑块开始相向滑动,初速度大小均为v0=3 m/s.A、B相遇时,A与木板恰好相对静止.设最大静摩擦力等于滑动摩擦力,取重力加速度大小g=10 m/s2.求:
(1)B与木板相对静止时,木板的速度;
(2)A、B开始运动时,两者之间的距离.
展开答案
【答案】(1)1 m/s,方向与B的初速度方向相同 (2)1.9 m
【解析】(1)滑块A和B在木板上滑动时,木板也在地面上滑动.设A、B和木板间所受的摩擦力的大小分别为f1、f2,木板与地面间的摩擦力的大小为f3,A、B、木板相对于地面的加速度大小分别是aA、aB和a1,在滑块B与木板达到共同速度前有:
$f_1=\mu _1m_Ag$…….①
$f_2=\mu_1m_Bg$……②
$f_3=\mu_2(m_A+m_B+m)g$……③
由牛顿第二定律得$f_1=m_Aa_A$……④
$f_2=m_Ba_B$……..⑤
$f_2-f_1-f_3=ma_1$…..⑥
设在t1时刻,B与木板达到共同速度,设大小为v1.由运动学公式有$v_1=v0-a_Bt_1$…..⑦
$v_1=a_1t_1$…….⑧
联立①②③④⑤⑥⑦⑧式,代入数据得v1=1 m/s,方向B的初速度方向相同.
(2)在t1时间间隔内,B相对于地面移动的距离为$s_B=v_0t_1-\dfrac{1}{2}a_B t_1^2$…..⑨
设在B与木板达到共同速度v1后,木板的加速度大小为a2,对于B与木板组成的体系,由牛顿第二定律有$f_1+f_3=(m_B+m)a_2$……⑩
由①②④⑤式知,aA=aB;再由⑦⑧可知,B与木板达到共同速度时,A的速度大小也为v1,但运动方向与木板相反,由题意知,A和B相遇时,A与木板的速度相同,设其大小为v2,设A的速度大小从v1变到v2所用的时间为t2,根据运动学公式,对木板有
$v_2=v_1-a_2t_2$…….⑪
对A有$v_2=-v_1+a_At_2$…..⑫
在t2时间间隔内,B(以及木板)相对地面移动的距离为$s_1=v_1t_2-\dfrac{1}{2}a_2t^2$…….⑬
在(t1+t2)时间间隔内,A相对地面移动的距离为$s_A=v_0(t_1+t_2)-\dfrac{1}{2}a_A(t_1+t_2)^2$…….⑭
A和B相遇时,A与木板的速度也恰好相同,因此A和B开始运动时,两者之间的距离为$s_0=s_A+s_1+s_B$…….⑮
联立以上各式,并代入数据得
s0=1.9 m.(也可用如图所示的速度—时间图象求解)
一长木板在水平地面上运动,在t=0时刻将一相对于地面静止的物块轻放到木板上,以后木板运动的速度一时间图象如图所示.已知物块与木板的质量相等,物块与木板间及木板与地面间均有摩擦,物块与木板间的最大静摩擦力等于滑动摩擦力,且物块始终在木板上.取重力加速度的大小g=10m/s2,求:
(1)物块与木板间的动摩擦因数μ1;
(2)木板与地面间的动摩擦因数μ2;
(3)从t=0时刻到物块与木板均停止运动时,物块相对于木板的位移的大小.
展开答案
【答案】(1)0.20;(2)0.30 ; (3)1.125 m
【解析】
试题分析:(1)从t=0 s时开始,木板与物块之间的摩擦力使物块加速,使木板减速,此过程一直持续到物块和木板具有共同速度为止。
由图可知,在t1=0.5 s时,物块和木板的速度相同。设t=0到t=t1时间间隔内,物块和木板的加速度大小分别为a1和a2,则:
$a_1=\dfrac{v_1}{t_1}$①
$a_2=\dfrac{v_0-v_1}{t_1}$②
式中v0=5 m/s、v1=1 m/s分别为木板在t=0、t=t1时速度的大小。
设物块和木板的质量为m,物块和木板间、木板与地面间的动摩擦因数分别为μ1、μ2,由牛顿第二定律得:
$\mu mg=ma_1 $③
$(\mu_1+2\mu_2)mg=ma_1$④
联立①②③④式得:⑤ μ1=0.20 ⑥μ2 =0.30
(2)在t1时刻后,地面对木板的摩擦力阻碍木板运动,物块与木板之间的摩擦力改变方向。设物块与木板之间的摩擦力大小为f,物块和木板的加速度大小分别为a1‘和a2‘,则由牛顿第二定律得:
$f=ma_1’$ ⑦
$2\mu_2mg-f=ma_2’$⑧
假设f<μ1mg,则a1‘=a2‘;由⑤⑥⑦⑧式得f=μ2mg>μ1mg,与假设矛盾。
故:$f=\mu_1mg$⑨
由⑦⑨式可知,物块加速度的大小等于a1;物块的v-t图像如图中点划线所示。由运动学公式可推知,物块和木板相对于地面的运动距离分别为:
$s_1=2\dfrac{v_1^2}{2a_1}$
$s_2=2\dfrac{v_0+v_1}{2}t_1 +\dfrac{v_1^2}{2a_2′}$,
物块相对于木板的位移的大小为:$s=s_2-s_1$
联立以上式解得:s=1.125 m
一轻弹簧的一端固定在倾角为θ的固定光滑斜面的底部,另一端和质量为m的小物块a相连,如图所示.质量为$\dfrac{3}{5}m$的小物块b紧靠a静止在斜面上,此时弹簧的压缩量为$x_0$,从t=0时开始,对b施加沿斜面向上的外力,使b始终做匀加速直线运动.经过一段时间后,物块a、b分离;再经过同样长的时间,b距其出发点的距离恰好也为$x_0$.弹簧的形变始终在弹性限度内,重力加速度大小为g.求:
(1)弹簧的劲度系数;
(2)物块b加速度的大小;
(3)在物块a、b分离前,外力大小随时间变化的关系式.
展开答案
【答案】 (1) 4 m/s (2) 4 m (3) 4.5 s
【解析】 (1)从A到B过程,根据牛顿第二定律有
$\mu_1mgcos 37°-mgsin 37°=ma_1$
解得:$a_1=0.4 m/s^2$
根据速度位移公式有$v_B^2-v_0^2=-2a_1L_1$
解得vB=4 m/s
(2)从B到静止过程,根据牛顿第二定律有$\mu_2mg=ma_2$
$0-v_B^2=-2a_2x_1$
解得x1=4 m
(3)从B到速度减为零的过程,根据运动学公式有
$t_1=\dfrac{0-v_B}{-a_2}s=2s$
从速度减为零开始向左运动过程
$v_2^2-0=2a__2x_2$,$x_2=1 m<4 m$
则箱子先匀加速1 m后匀速运动$t_2=\dfrac{v_2-0}{a_2}=1s$
匀速运动到B过程x3=x1-x2=3 m,$t_3=\dfrac{x_3}{v_2}=1.5s$
因为μ1mgcos 37°>mgsin 37°,所以箱子最后会停在斜面上,t总=t1+t2+t3=4.5 s.
(2021·四川双流中学6月月考)如图所示,质量为m0=20 kg的长木板静止在水平面上,质量m=10 kg的小木块(可视为质点)以v0=4.5 m/s的速度从木板的左端水平滑到木板上,小木块最后恰好没有滑出长木板。已知小木块与木板间的动摩擦因数为μ1=0.4,木板与水平地面间的动摩擦因数为μ2=0.1,最大静摩擦力等于滑动摩擦力,重力加速度g=10 m/s2。求:
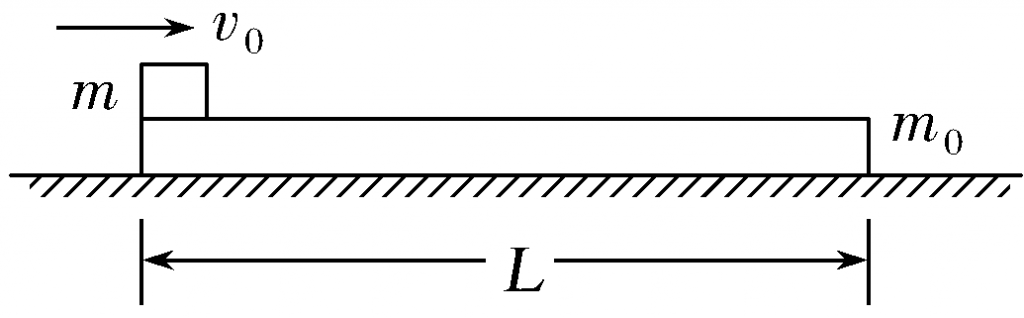
(1)木块刚滑上木板时木块、木板的加速度大小;
(2)木板的长度L;
(3)木板的运动时间及木块运动的位移大小。
展开答案
【答案】 (1)4 m/s2 0.5 m/s2 (2)2.25 m (3)1.5 s 2.625 m
【解析】 (1)对木块受力分析知木块做减速运动,设其加速度大小为a1,则由牛顿第二定律可得
$\mu_1mg=ma_1$(1分)
代入数据解得a1=4 m/s2(1分)
对木板受力分析,设木板加速度大小为a2,由牛顿第二定律可得
$\mu_1mg-\mu_2(m+m_0)g=m_0a_2$(2分)
代入数据解得a2=0.5 m/s2(2分)
(2)设经过时间t1二者共速,则有
$v_0-a_1t_1=a_2t_1$(1分)
解得$t_1=1 s$(1分)
设其共速时的速度大小为v1,则有v1=a2t1,
解得v1=0.5 m/s(1分)
t1时间内木块的位移为$x_1=\dfrac{v_0+v_1}{2}t_1$(1分)
解得x1=2.5 m(1分)
木板的位移为$x_2=\dfrac{v_1}{2}t_1$(1分)
解得x2=0.25 m(1分)
所以木板的长度为$L=x_1-x_2=2.25 m$(1分)
(3)木块与木板共速后,二者一起减速运动,加速度大小为
$a_3=μ2g=1 m/s^2$(1分)
设再经过时间t2停止,则有$v_1=a_3t_2$(1分)
代入数据解得$t_2=0.5 s$(1分)
故木块运动的总时间为$t=t_1+t_2=1.5 s$(1分)
木块运动的总位移为$x=x_1+\dfrac{v_1}{2}t_2$(1分)
解得x=2.625 m(1分)
某粮库使用额定电压$U=380V$,内阻$R=0.25Ω$的电动机运粮,如图所示,配重和电动机连接小车的缆绳均平行于斜坡,装满粮食的小车以速度$v=2m/s$沿斜坡匀速上行,此时电流$I=40A$,关闭电动机后,小车又沿斜坡上行路程L到达卸粮点时,速度恰好为零。卸粮后,给小车一个向下的初速度,小车沿斜坡刚好匀速下行。已知小车质量$m_1=100kg$,车上粮食质量$m_2=1200kg$,配重质量$m_0=40kg$,取重力加速度$g=10m/s$,小车运动时受到的摩擦阻力与车及车上粮食总重力成正比,比例系数为 $k$,配重始终未接触地面,不计电动机自身机械摩擦损耗及缆绳质量。求:
(1)比例系数$k$值;
(2)上行路程$L$值。
【答案】(1)、0.1 (2)、$\dfrac{13}{37}$
【解析】本题考点有二,一个是电动机的非纯电阻电路的计算,第二就是斜面平衡问题。
难点在于计算要细心,而细心是要靠计算的流程,只有掌握了流程,并且严格执行,才能一次计算正确。
根据上升和下降时都是匀速,可以得出以下方程,假设角度是$\theta$
$P_出=Fv=UI-I^2R$
$F+m_0g=(m_1+m_2)gsin\theta+k(m_1+m_2)g$
$m_1gsin\theta=km_1g+m_0g$
先检查一下上面的等式有没有问题,然后带入正确的数字,检查之后才能进行计算。
$2F=380\times40-40\times40\times\dfrac{1}{4}$
$F=370\times20$
$1300\times 10 \times sin\theta + k1300 \times 10 =400+370\times 20$
同时除100
$13 \times 10\times sin\theta +k13\times10=39\times2$
$10\times sin\theta=10k+4$
$sin\theta=\dfrac{1}{2}$
$a=\dfrac{74}{13}$
(2)
$a(m_1+m_2)=(m_1+m_2)gsin\theta+k(m_1+m_2)g-m_0g$
$v^2=2aL$
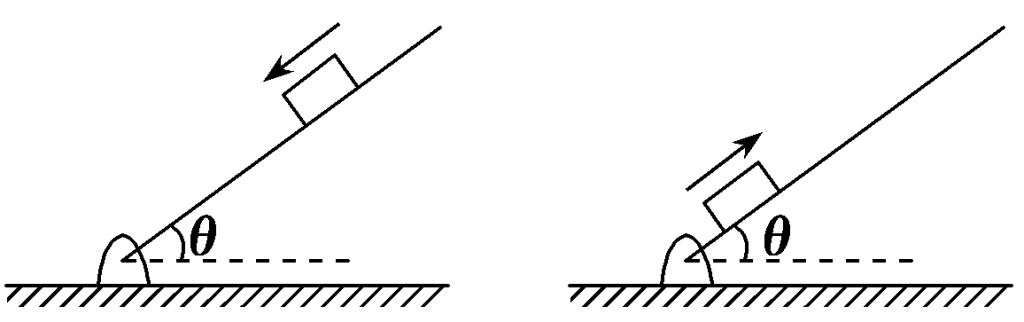
如图所示,木板与水平地面间的夹角θ可以随意改变,当θ=30°时,可视为质点的一小木块恰好能沿着木板匀速下滑。若让该小木块从木板的底端以大小恒定的初速率v0沿木板向上运动,随着θ的改变,小木块沿木板向上滑行的距离x将发生变化,重力加速度为g。
(1)求小木块与木板间的动摩擦因数;
(2)当θ角为何值时,小木块沿木板向上滑行的距离最小,并求出此最小值。
展开答案
【答案】(1)$\dfrac{\sqrt{3}}{3}$ ;(2)60°,$\dfrac{\sqrt{3}v_0^2}{4g}$
【解析】解:(1)当θ=30°时,木块处于平衡状态,对木块受力分析
$mgsin\theta$=\mu F_N$
$F_N-mgcos\theta=0$解得
$\mu=tan \theta =tan 30°=\dfrac{sqrt{3}}{3}$
(2)当θ变化时,设沿斜面向上为正方向,木块的加速度为a,则
$-mgsin \theta – \mu mgcos \theta=ma$
由
$0-v_0^2=2ax$
得
$x=\dfrac{v_0^2}{2g(sin \theta + \mu cos \theta)}=\dfrac{v_0^2}{2g\sqrt{1+\mu^2}sin(\theta+a)}$
其中tan α=μ,则当α+θ=90°时x最小,即θ=60°,所以x最小值
$x_{min}=\dfrac{v_0^2}{2g(sin60°+\mu cos60°)}=\dfrac{\sqrt{3}v_0^2}{4g}$
如图所示,一个质量为M长为L的圆管竖直放置,顶端塞有一个质量为m的弹性小球,M=4m,球和管间的滑动摩擦力和最大静摩擦力大小均为4mg.管从下端离地面距离为H处自由落下,运动过程中,管始终保持竖直,每次落地后向上弹起的速度与落地时速度大小相等,不计空气阻力,重力加速度为g.求:
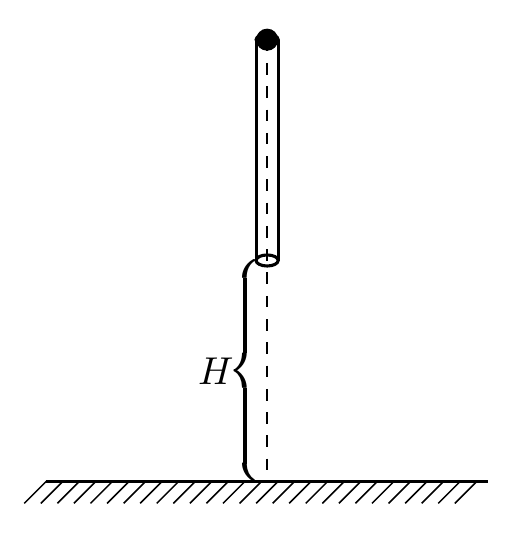
(1)管第一次落地弹起时管和球的加速度;
(2)管第一次落地弹起后,若球没有从管中滑出,则球与管达到相同速度时,管上升的最大高度。
(3)管第二次弹起后球不致滑落,L应满足什么条件.
展开答案
(1)管第一次落地弹起时,管瞬间向上运动,受到自身重力以及摩擦力,所以管的加速度$a_1=\dfrac{4mg+4mg}{4m}=2g$方向向下。球受到向上的摩擦力和向下的重力,球加速度$a_2=\dfrac{f-mg}{m}=\dfrac{4mg-mg}{m}=3g$方向向上。
(2)取竖直向下为正方向.球与管第一次碰地时速度$v_0=\sqrt{2gH}$ ,方向向下.碰地后管的速度$v_1=- \sqrt{2gH}$,方向向上;球的速度$v_2=\sqrt{2gH}$,方向向下若球刚好没有从管中滑出,设经过时间$t_1$,球管速度v相同,则有
$$-v_1+a_1t_1=v_2-a_2 {t_1}^2$$
$$-\sqrt{2gH}-2gt_1=\sqrt{2gH}+3mgt_1$$
$$2\sqrt{2gH}=5mgt_1$$
$$t_1=\frac{2}{5}\sqrt{\frac{2H}{g}}$$
此时管下端的高度为$h_1=v_0 t_1-\frac{1}{2} {a_1} {t_1}^2$ 带入数据
$$h_1=\frac{12}{25}H$$
此后管和球共速上升$v_g=v_0-a_2 t_1=\frac{1}{5} \sqrt{2gH}$
共速上升的高度 $$h_2=\frac{v_g ^2}{2g}=\frac{1}{25}H$$
管上升的最大高度$H_1$$$H_1=h_1+h_2=\frac{13}{25}H $$
(3)设第一次弹起过程中球相对于管的位移$x_1$,在管开始下落到上升到$H_1$的过程中,由动能减少量等于摩擦力做功
$$Mg(H-H_1+mg(H-h_1 + x_1)-4mg x_1=0$$
$$x_1= \frac{4}{5}H_1$$
即L应满足条件$x_1 +x_2 \leq L$
$$\frac{4}{5}H +\frac{4}{5}H_1\leq L$$
$$\frac{4}{5}H +\frac{4}{5} \frac{13}{25}H\leq L$$
$$\frac{152}{125}H\leq L$$
