牛顿定律经典例题
某工地小型升降电梯的原理图如图所示,轿厢A、对重B通过跨过轻质定滑轮的足够长轻质缆绳连接,电机通过轻质缆绳拉动对重,使轿厢由静止开始向上运动,运动过程中A未接触滑轮、B未落地。已知A、B质量分别为M=600 kg、m=400 kg,电机输出功率恒为P=3kW,不考虑空气阻力与摩擦阻力,重力加速度g取10m/S²,则当轿厢速度为1m/s时,A、B之间轻质缆绳的拉力大小为( )
A.5 400 N
B.6 000 N
C.6 600 N
D.7 000 N
展开答案
【答案】C
【解析】电机的力$F_B=\dfrac{P}{v}=3000N$
$F_B+mg-F_T=ma$
$F_T-Mg=Ma$
解得$F_T=6600N$
(多选)如图所示,劲度系数为k的轻弹簧竖直放置,下端固定在水平地面上。一质量为m的小球,从离弹簧上端高h处自由下落,接触弹簧后继续向下运动。小球从开始下落到小球第一次运动到最低点的过程中,下列关于小球的速度v、加速度a随时间t变化的图象中符合实际情况的是( )
展开答案
【答案】 AD
【解析】 在小球下落的开始阶段,小球做自由落体运动,加速度为g;接触弹簧后,开始时重力大于弹力,加速度方向向下,随着小球的不断下降,弹力逐渐变大,故小球做加速度减小的加速运动,某时刻加速度可减小到零,此时速度最大;小球继续下落时,弹力大于重力,加速度方向变为向上,且加速度逐渐变大,直到速度减小到零,到达最低点,由对称知识可知,到达最低点的加速度大于g,故A、D正确。
如图1,A、B、C三个小球质量均为m,A、B之间用一根没有弹性的轻质细线连在一起,B、C之间用轻弹簧拴接,整个系统用细线悬挂在天花板上并且处于静止状态。现将A上面的细线剪断,则在剪断细线的瞬间,A、B、C三个小球的加速度分别是(重力加速度为g)( )
A.1.5g,1.5g,0 B.g,2g,0 C.g,g,g D.g,g,0
展开答案
【答案】 A
【解析】 剪断细线前,由共点力的平衡条件可知,A上面的细线的拉力为3mg,A、B之间细线的拉力为2mg,轻弹簧的拉力为mg。在剪断A上面的细线的瞬间,轻弹簧中拉力不变,小球C所受合力为零,所以C的加速度为零;A、B小球被细线拴在一起,整体受到二者重力和轻弹簧向下的拉力,由牛顿第二定律得3mg=2ma,解得a=1.5g,选项A正确。
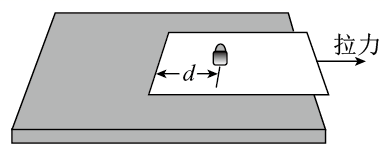
如图所示,将小砝码置于桌面上的薄纸板上,用水平向右的拉力将纸板迅速抽出,砝码的移动很小,几乎观察不到,这就是大家熟悉的惯性演示实验。若砝码和纸板的质量分别为2m和m,各接触面间的动摩擦因数均为μ。重力加速度为g,最大静摩擦力等于滑动摩擦力。要使纸板相对砝码运动,所需拉力的大小应大于( )
A.3μmg B.4μmg C.5μmg D.6μmg
展开答案
【答案】D
【解析】当纸板相对砝码运动时,设砝码的加速度为a1,纸板的加速度为a2,根据牛顿第二定律,对砝码有
f1=μ·2mg=2ma1
解得
a1=μg
对纸板有
F-f1-f2=ma2
其中
f2=μ·3mg
二者发生相对运动需要纸板的加速度大于砝码的加速度,即
a2>a1
所以
F=f1+f2+ma2>f1+f2+ma1=μ·2mg+μ·3mg+μmg=6μmg
即
F>6μmg
D正确。
如图甲所示,一轻质弹簧的下端固定在水平面上,上端叠放两个质量均为M的物体A、B(B物体与弹簧连接),弹簧的劲度系数为k,初始时物体处于静止状态.现用竖直向上的 拉力F作用在物体A上,使物体A开始向上做加速度为a的匀加速运动,测得两个物体的v—t图像如图乙所示(重力加速度为g),则
A.施加外力前,弹簧的形变量为$\dfrac{2g}{k}$
B.外力施加的瞬间A、B间的弹力大小为M(g–a)
C.A、B 在t1时刻分离,此时弹簧弹力恰好为零
D.弹簧恢复到原长时,物体B的速度达到最大值
展开答案
【答案】B
【解析】A.施加F前,物体AB整体平衡,根据平衡条件有:
2Mg=kx
解得:
$x=\dfrac{2mg}{k}$
故A错误;
解法一:这是一个相对违法直觉的,所以我们先看一种情况。
我们看到中间的弹力是由最小力决定的,所以B对A的弹力开始是mg,A向上加速,所以等于失去了F的力,所以他们之间的弹力只有m(g-a)
解法二:施加外力F 的瞬间,对B 物体,根据牛顿第二定律有:
$F_弹-Mg-F_AB=Ma$
其中
$F_弹=2Mg$
解得:
$F_AB=M(g-a)$
C.物体A、B在t1时刻分离,此时A、B具有共同的v与a;且$F_AB=0$;对B:
$F_弹’-Mg=Ma$
解得:
$F_弹’=M(g-a)$
弹力不为零,故C错误;
D.而弹簧恢复到原长时,B受到的合力为重力,已经减速一段时间;速度不是最大值;故D错误。
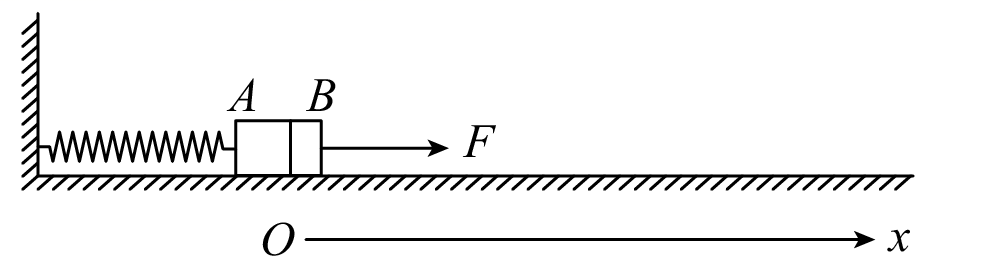
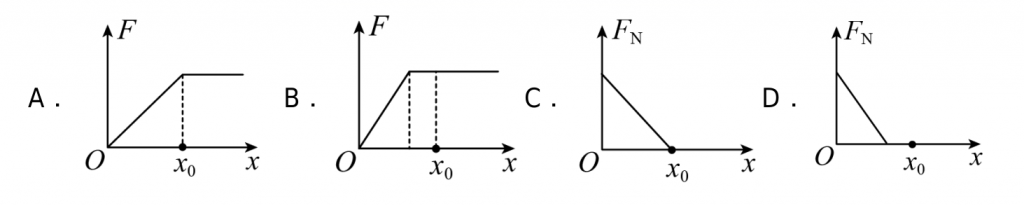
如图所示,光滑水平地面上,可视为质点的两滑块A、B在水平外力作用下紧靠在一起压紧弹簧,弹簧左端固定在墙壁上,此时弹簧的压缩量为x0,以两滑块此时的位置为坐标原点建立如图所示的一维坐标系。现将外力突然反向并使B向右做匀加速运动,下列关于拉力F、两滑块间弹力FN与滑块B的位移x关系的图象可能正确的是( )
展开答案
【答案】BD
【解析】当A和B相对静止加速时,对A、B整体,由牛顿第二定律得
F+k(x0-x)=(mA+mB)a
因为可能有
kx0=(mA+mB)a
则得
F=kx
即Fx图象可能为过原点的直线,当A、B分离时,对A
k(x0-x)=mAa
此时x<x0,当A、B分离后,对B,F=mBa大小恒定,与x无关,在A、B分离前,对A
k(x0-x)-FN=mAa
分离后
FN=0
故选BD。
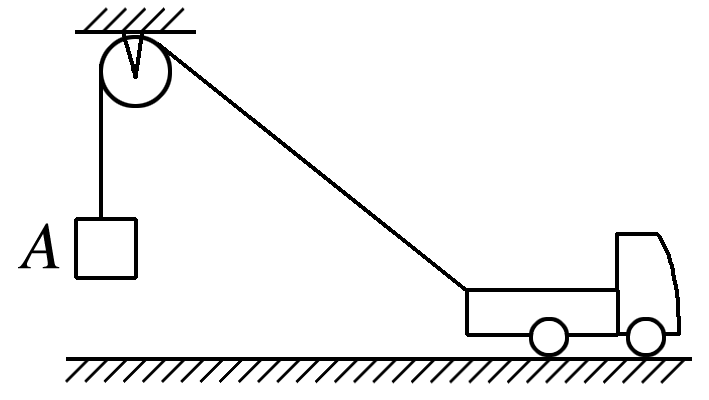
如图所示,汽车用跨过定滑轮的轻绳提升物块A。汽车匀速向右运动,在物块A到达滑轮之前,关于物块A,下列说法正确的是( )
A.将竖直向上做匀速运动
B.将处于超重状态
C.将处于失重状态
D.将竖直向上先加速后减速
展开答案
【答案】B
【解析】如果凭直觉,可能会有人选出正确答案,但是物理不能仅仅凭借直觉,还需要把直觉变成一个规律,并且让其有使用所有情形的公式,只有这种思想才能让我们的物理越来越简单,也会让一门学问越来越系统化。
这里涉及一个速度的合成与分解,原理只有一条,平行四边形原则。速度和力一样是可以进行分解的,而分解的原理和力一样,于是我们可以推断,所有的矢量都是可以平行变形原则分解。
力的方向限定了分解的方式,固定了分解的结果,速度的分解也是类似,汽车的移动方向和绳子的方向也限定了速度的分解。
$v_绳子= vcos\theta$ 角度变大绳子的速度变大,所以选B
这就是物理的魅力所在。
如图所示,50个大小相同、质量均为m的小物块,在平行于斜面向上的恒力F 作用下一起沿斜面向上运动.已知斜面足够长,倾角为30°,各物块与斜面的动摩擦因数相同,重力加速度为 g,则第48个小物块对第49个小物块的作用力大小为( )
A.$\dfrac{24}{25}F$F B.$\dfrac{1}{25}F$
C.$24mg+\dfrac{F}{2}$ D.因为动摩擦因数未知,所以不能确定
展开答案
【答案】B
【解析】zuijia fangan ztf
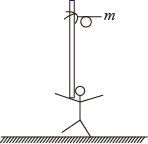
如图所示为杂技“顶竿”表演,一人站在地上,肩上扛一质量为M的竖直竹竿,竿上有一质量为m的人可以看成质点,当此人沿着竖直竿以加速度a加速下滑时,竿对地面上的人的压力大小为( )
A.(M+m)g+ma B.(M+m)g–ma
C.(M+m)g D.(M–m)g
展开答案
【答案】B
【解析】对竹竿上的人由牛顿第二定律知
$mg-f=ma$
所以
$f=m(g-a)$
由牛顿第三定律知竹竿上的人对竹竿的摩擦力竖直向下,对竹竿由平衡条件知
$Mg+f’=F_N$
$f=f’$
由牛顿第三定律知竹竿对底人的压力
$F_N=(M+m)g-ma$
故B正确ACD错误,习惯用方程的方式解决问题
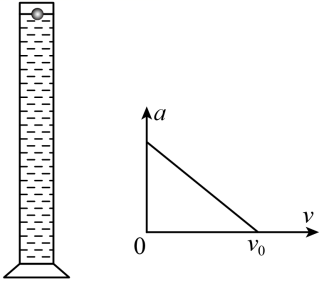
如图所示,一竖直放置的足够长的玻璃管中装满某种液体,一半径为r、质量为m的金属小球,从t=0时刻起,由液面静止释放,小球在液体中下落,其加速度a随速度v的变化规律如图所示。已知小球在液体中受到的阻力$f=6\pi \eta vr$,式中r是小球的半径,v是小球的速度,η是常数。忽略小球在液体中受到的浮力,下列说法正确的是( )。
A.小球的最大加速度为g
B.小球的速度从0增加到v0的过程中,做匀变速运动
C.小球先做加速度减小的变加速运动,后做匀速运动
D.小球的最大速度为$\dfrac{mg}{6\pi\eta r}$
展开答案
【答案】ACD
【解析】A.当t=0时,小球所受的阻力f=0,此时加速度为g,A正确; 看似难得题目往往很简单
B.随着小球速度的增加,加速度减小,小球的速度从0增加到v0的过程中,加速度减小,B错误;
CD.根据牛顿第二定律有
$mg-f=ma$
解得
$a=g-\dfrac{6\pi \eta vr}{m}$
当a=0时,速度最大,此后小球做匀速运动,最大速度
$v_m=$\dfrac{mg}{6\Pi\eta r}$
C、D正确。
(2011·福建高考真题)如图,一不可伸长的轻质细绳跨过滑轮后,两端分别悬挂质量为m1和m2的物体A和B,若滑轮有一定大小,质量为m且分布均匀,滑轮转动时与绳之间无相对滑动,不计滑轮与轴之间的摩擦.设细绳对A和B的拉力大小分别为T1和T2,已知下列四个关于T1的表达式中有一个是正确的,请你根据所学的物理知识,通过一定的分析,判断正确的表达式是( )
A.$T_1=\dfrac{(m+2m_2)m_1g}{m+2(m_1+m_2)}$
B.$T_1=\dfrac{(m+2m_2)m_1g}{m+4(m_1+m_2)}$
C.$T_1=\dfrac{(m+4m_2)m_1g}{m+2(m_1+m_2)}$
D.$T_1=\dfrac{(m+4m_2)m_1g}{m+4(m_1+m_2)}$
展开答案
【答案】 C
【解析】M=0带入即可
