理想气体与热力学定律

---

1.分子动理论要掌握的“一个桥梁、三个核心”

1宏观量与微观量的转换桥梁

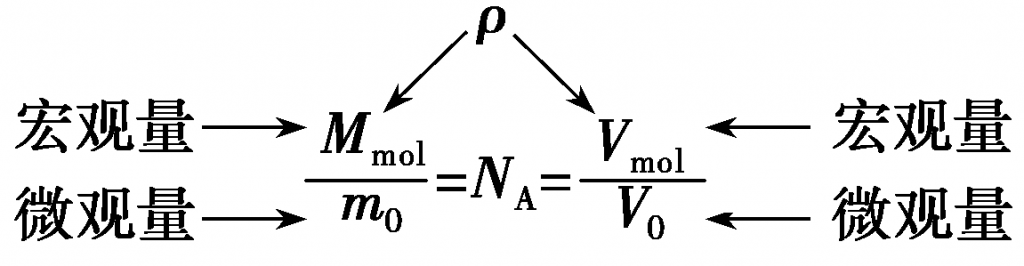
(1)分子的直径(视为球模型)：数量级为10^－10 m；

(2)分子的质量：数量级为10^－26 kg.

2.阿伏加德罗常数

(1)1 mol的任何物质都含有相同的粒子数.通常可取N_A＝6.02×10²³ mol^－1；

(2)阿伏加德罗常数是联系宏观物理量和微观物理量的桥梁.

3.微观量与宏观量

(1)微观量：分子质量m₀、分子体积V₀、分子直径d等.

(2)宏观量：物体的质量m、摩尔质量M、物体的密度ρ、物体的体积V、摩尔体积V_mol等.

4.分子的两种模型

(1)球模型：$v_0=\dfrac{1}{6}\pi d^3$，得直径$d=^3\sqrt{\dfrac{6v_0}{\pi}}$(常用于固体和液体).

(2)立方体模型：$v_0=d^3$，得边长$d=^3\sqrt{v_)}$(常用于气体).

5.几个重要关系

(1)一个分子的质量：$m_0=\dfrac{M}{N_A}$

(2)一个分子的体积：$V_0=\dfrac{V_{mol}}{N_A}$(注意：对于气体，V₀表示一个气体分子占有的空间).

(3)1 mol物体的体积：$V_{mol}=\dfrac{M}{P}$

(3)分子运动：分子永不停息地做无规则运动，温度越高，分子的无规则运动越剧烈，即平均速率越大，但某个分子的瞬时速率不一定大．

(4)分子势能、分子力与分子间距离的关系．

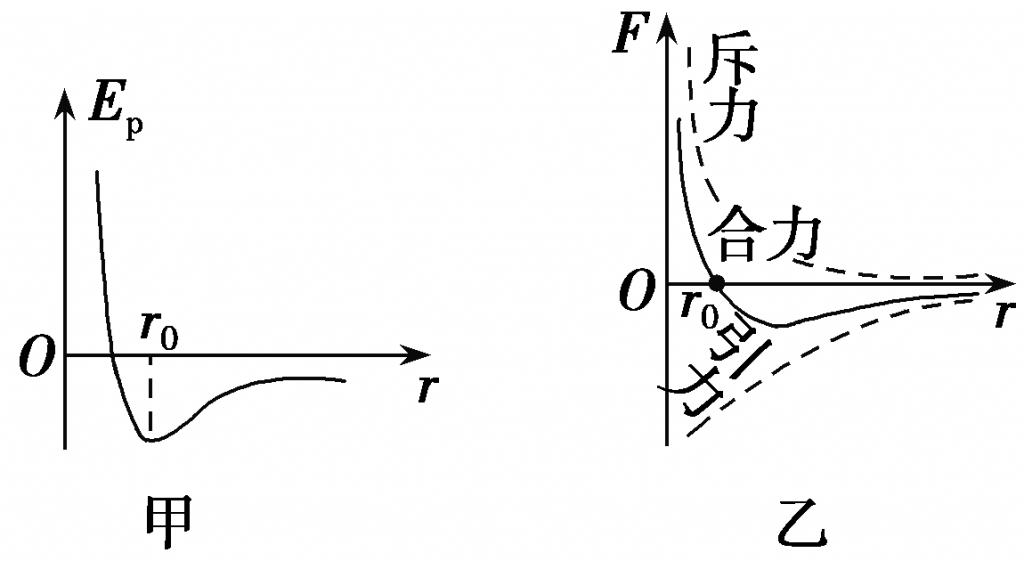
2.理想气体相关三量$\Delta U$、$W$、$Q$的分析思路

(1)内能变化量$\Delta U$的分析思路

①由气体温度变化分析气体内能变化．温度升高，内能增加；温度降低，内能减少．

②由公式$\Delta U=W+Q$分析内能变化．

(2)做功情况W的分析思路

①由体积变化分析气体做功情况．体积膨胀，气体对外界做功；体积被压缩，外界对气体做功．

②由公式$W=\Delta U-Q$分析气体做功情况．

(3)气体吸、放热Q的分析思路：一般由公式$Q=\Delta U-W$ 分析气体的吸、放热情况．

---

---

1．固体和液体的主要特点

(1)晶体和非晶体的分子结构不同，表现出的物理性质不同．晶体具有确定的熔点，单晶体表现出各向异性，多晶体和非晶体表现出各向同性．晶体和非晶体在适当的条件下可以相互转化．

(2)液晶是一种特殊的物质状态，所处的状态介于固态和液态之间，液晶具有流动性，在光学、电学物理性质上表现出各向异性．

(3)液体的表面张力使液体表面具有收缩到最小的趋势，表面张力的方向跟液面相切．

2．饱和汽压的特点

液体的饱和汽压与温度有关，温度越高，饱和汽压越大，且饱和汽压与饱和汽的体积无关．

3.相对湿度

某温度时空气中水蒸气的压强与同一温度时水的饱和汽压之比．即$B=\dfrac{p}{p_s}$.

4．对气体压强的两点理解

(1)气体对容器壁的压强是气体分子频繁碰撞的结果，温度越高，气体分子数密度越大，气体对容器壁因碰撞而产生的压强就越大．

(2)地球表面大气压强可认为是大气重力产生的．

(1)内能的变化都要用热力学第一定律进行综合分析。

(2)做功情况看气体的体积：体积增大，气体对外做功，W为负；体积缩小，外界对气体做功，W为正。

(3)与外界绝热，则不发生热传递，此时Q＝0。

(4)如果研究对象是理想气体，因理想气体忽略分子势能，所以当它的内能变化时，主要体现在分子动能的变化上，从宏观上看就是温度发生了变化。

---

---

(1)充气问题

设想将充进容器内的气体用一个无形的弹性口袋收集起来，那么当我们取容器和口袋内的全部气体为研究对象时，这些气体状态不管怎样变化，其质量总是不变的．这样，就将变质量问题转化为定质量问题．

(2)抽气问题

用抽气筒对容器抽气的过程中，对每一次抽气而言，气体质量发生变化，其解决方法同充气问题类似，假设把每次抽出的气体包含在气体变化的始末状态中，即把变质量问题转化为定质量问题．

(3)灌气(分装)问题

将一个大容器里的气体分装到多个小容器中的问题，可以把大容器中的气体和多个小容器中的气体看作整体作为研究对象，可将变质量问题转化为定质量问题．

(4)漏气问题

容器漏气过程中气体的质量不断发生变化，不能用理想气体状态方程求解．如果选容器内剩余气体为研究对象，可将变质量问题转化为定质量问题．

---

---

1．一定质量的理想气体的状态变化图象与特点

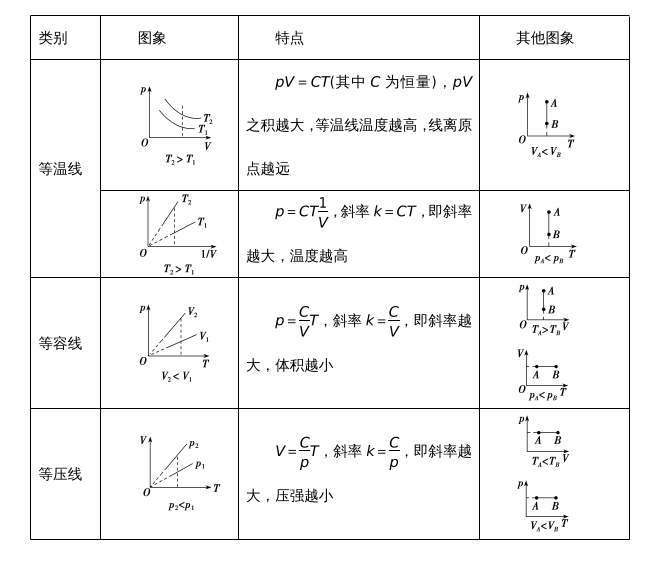
2.对热力学第一定律的考查有定性判断和定量计算两种方式

(1)定性判断

利用题中的条件和符号法则对W、Q、ΔU中的其中两个量做出准确的符号判断，然后利用ΔU＝W＋Q对第三个量做出判断．

(2)定量计算

一般计算等压变化过程的功，即W＝p·ΔV，然后结合其他条件，利用ΔU＝W＋Q进行相关计算．

(3)注意符号正负的规定

若研究对象为气体，对气体做功的正负由气体体积的变化决定．气体体积增大，气体对外界做功，W<0；气体的体积减小，外界对气体做功，W>0.