机械振动与机械波
1.简谐运动
(1)定义:物体在跟偏离平衡位置的位移大小成正比,并且总是指向平衡位置的回复力的作用下的振动,叫做简谐运动.
描述简谐运动的物理量
①位移x:由平衡位置指向振动质点所在位置的有向线段,是矢量,其最大值等于振幅。
②振幅A:振动物体离开平衡位置的最大距离,是标量,表示振动的强弱。
③周期T和频率f:表示振动快慢的物理量,二者互为倒数关系,即$T=\dfrac{1}{f}$。
(2)简谐运动的“五个特征”
①.动力学特征:$F=-kx$,“-”表示回复力的方向与位移方向相反,$k$是比例系数,不一定是弹簧的劲度系数。
②.运动学特征:简谐运动的加速度的大小与物体偏离平衡位置的位移的大小成正比,而方向相反,为变加速运动,远离平衡位置时,$x、F、a、E_p$均增大,$v、E_k$均减小,靠近平衡位置时则相反。

③.运动的周期性特征:相隔T 或nT 的两个时刻,振子处于同一位置且振动状态相同。
④.对称性特征
(1).相隔$\dfrac{T}{2}$ 或 $\dfrac{(2N+1)}{2}T($(n为正整数)的两个时刻,振子位置关于平衡位置对称,位移、速度、加速度大小相等,方向相反。
(2).如图所示,振子经过关于平衡位置O 对称的两点P、P′(OP=OP′)时,速度的大小、动能、势能相等,相对于平衡位置的位移大小相等。
(3).振子由P到O所用时间等于由O到P′所用时间,即tPO=tOP′。
(4).振子往复过程中通过同一段路程(如OP段)所用时间相等,即tOP=tPO。
⑤.能量特征:振动的能量包括动能Ek和势能Ep,简谐运动过程中,系统动能与势能相互转化,系统的机械能守恒。
(3)简谐运动图像的理解和应用
(1).简谐运动的数学表达式
x=Asin(ωt+φ)
(2).根据简谐运动图象可获取的信息
①确定振动的振幅A和周期T。
$T=\dfrac{2\pi}{\omega}$
②确定振动物体在任一时刻的位移。
$x=Asin(\omega t+\varphi)$
带入$t$具体数值就可以求出任意时刻的位移。
③确定各时刻质点的振动方向。
判断方法:振动方向可以根据下一时刻位移的变化来判定。下一时刻位移若增加,质点的振动方向是远离平衡位置;下一时刻位移如果减小,质点的振动方向指向平衡位置。
2.弹簧振子
周期和频率只取决于弹簧的劲度系数和振子的质量,与其放置的环境和放置的方式无任何关系。如某一弹簧振子做简谐运动时的周期为T,不管把它放在地球上、月球上还是卫星中;是水平放置、倾斜放置还是竖直放置;振幅是大还是小,它的周期就都是T。
3.单摆:
摆线的质量不计且不可伸长,摆球的直径比摆线的长度小得多,摆球可视为质点.单摆是一种理想化模型。
(1)单摆的振动可看作简谐运动的条件是:最大摆角α<5°.
(2)单摆的回复力是重力沿圆弧切线方向并且指向平衡位置的分力.
(3)作简谐运动的单摆的周期公式为::$T=2\pi \sqrt{\dfrac{L}{g}}$
猜想,一般震动的频率均和震动物体的长度有关,越长频率越低,比如钢琴,二胡,单摆,笛子等等。.
4.受迫振动
(1)受迫振动:振动系统在周期性驱动力作用下的振动叫受迫振动.
(2)受迫振动的特点:受迫振动稳定时,系统振动的频率等于驱动力的频率,跟系统的固有频率无关.
(3)共振:当驱动力的频率=振动系统的固有频率时,振动物体的振幅最大,这种现象叫做共振。共振的条件:驱动力的频率等于振动系统的固有频率.
5.机械波:机械振动在介质中的传播形成机械波.
(1)机械波产生的条件:①波源;②介质
(2)机械波的分类
①横波:质点振动方向与波的传播方向垂直的波叫横波.横波有凸部(波峰)和凹部(波谷).
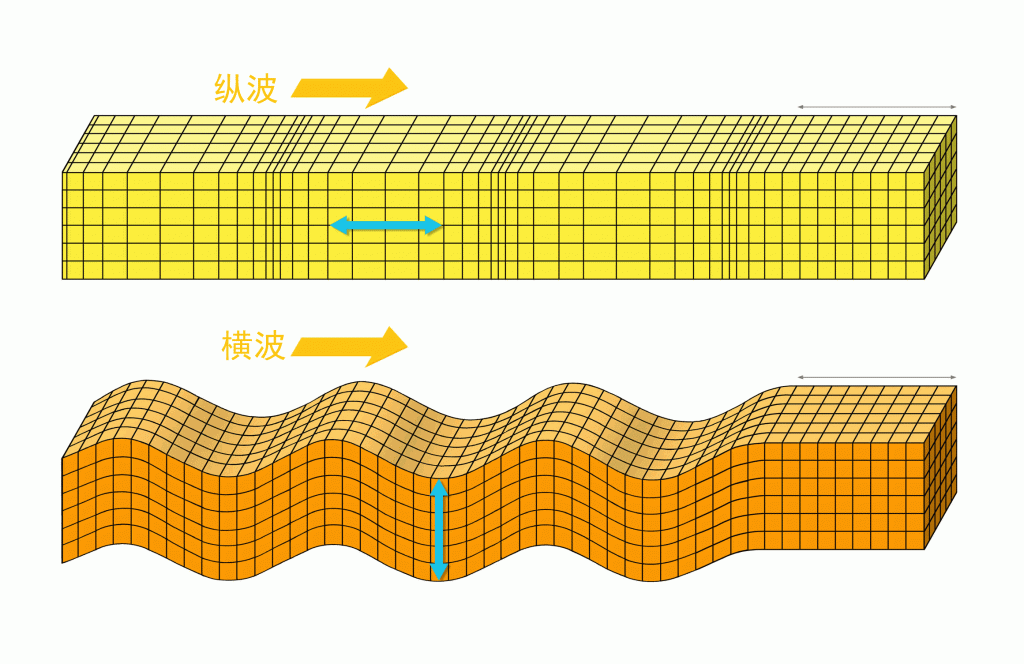
②纵波:质点振动方向与波的传播方向在同一直线上的波叫纵波.纵波有密部和疏部. [注意]气体、液体、固体都能传播纵波,但气体、液体不能传播横波.

(3)机械波的特点 ①机械波传播的是振动形式和能量.质点只在各自的平衡位置附近振动,并不随波迁移. ②介质中各质点的振动周期和频率都与波源的振动周期和频率相同.③离波源近的质点带动离波源远的 质点依次振动.
6.波长、波速和频率及其关系
(1)波长:两个相邻的且在振动过程中对平衡位置的位移总是相等的质点间的距离叫波长.振动在一个周期里在介质中传播的距离等于一个波长.
(2)波速:波的传播速率.机械波的传播速率由介质决定,与波源无关.
(3)频率:波的频率始终等于波源的振动频率,与介质无关.
(4)三者关系:$v=λf$
7. 波动图像:表示波的传播方向上,介质中的各个质点在同一时刻相对平衡位置的位移.当波源作简谐运动时,它在介质中形成简谐波,其波动图像为正弦或余弦曲线.
(1)由波的图像可获取的信息 ①从图像可以直接读出振幅(注意单位).②从图像可以直接读出波长(注意单位). ③可求任一点在该时刻相对平衡位置的位移(包括大小和方向) ④在波速方向已知(或已知波源方位)时可确定各质点在该时刻的振动方向.⑤可以确定各质点振动的加速度方向(加速度总是指向平衡位置)
(2)波动图像与振动图像的比较:
| 图像类型 | 振动图像 | 波的图像 |
| 研究对象 | 一个振动的质点 | 沿波传播方向上所有的质点 |
| 研究内容 | 一个质点的位移随时间变化规律 | 某时刻所有质点的空间分布规律 |
| 图像 | ||
| 物理意义 | 质点各个时刻的位移 | 某时刻质点的位移 |
| 图像信息 | 1、质点振动周期 2、质点振幅 3、各时刻质点位移 4、各时刻质点速度、加速度方向 | 1、波长、振幅 2、任意一质点在该时刻的位移 3、任意一质点在该时刻加速度方向 4、传播方向、振动方向的互判 |
| 图像变化 | 随时间推移,图像延续,但已有形状不变 | 随时间推移,图像传播方向平移。 |
| 一个完整曲线占横坐标的距离 | 表示一个周期 | 表示一个波长 |
8.波动问题多解性
波动图像与振动图像的比较:波的传播过程中时间上的周期性、空间上的周期性以及传播方向上的双向性是导致“波动问题多解性”的主要原因.若题目假设一定的条件,可使无限系列解转化为有限或惟一解。
9.波的衍射
波在传播过程中偏离直线传播,绕过障碍物的现象。衍射现象总是存在的,只有明显与不明显的差异.波发生明显衍射现象的条件是;障碍物(或小孔)的尺寸比波的波长小或能够与波长差不多。
10.波的叠加
几列波相遇时,每列波能够保持各自的状态继续传播而不互相干扰,只是在重叠的区域里,任一质点的总位移等于各列波分别引起的位移的矢量和。
两列波相遇前、相遇过程中、相遇后,各自的运动状态不发生任何变化,这是波的独立性原理.
11.波的干涉:
频率相同的两列波叠加,某些区域的振动加强,某些区域的振动减弱,并且振动加强和振动减弱的区域相互间隔的现象,叫波的干涉。产生干涉现象的条件;两列波的频率相同,振动情况稳定。[注意]干涉时,振动加强区域或振动减弱区域的空间位置是不变的。
加强区域中心质点的振幅等于两列波的振幅之和,减弱区域中心质点的振幅等于两列波的振幅之差. ②两列波在空间相遇发生干涉,两列波的波峰相遇点为加强点,波峰和波谷的相遇点是减弱的点,加强的点只是振幅大了,并非任一时刻的位移都大;减弱的点只是振幅小了,也并非任一时刻的位移都最小. 如图若SA、SB为振动方向同步的相干波源,当PSA-PSB=nλ时,振动加强;当PSA-PSB=(2n+1)λ/2时,振动减弱。
12.声波
(1)空气中的声波是纵波,传播速度为340m/s. (2)能够引起人耳感觉的声波频率范围是:20~2Hz.
(3)超声波:频率高于2Hz的声波. ①超声波的重要性质有:波长短,不容易发生衍射,基本上能直线传播,因此可以使能量定向集中传播;穿透能力强.②对超声波的利用:用声纳探测潜艇、鱼群,探察金属内部的缺陷;利用超声波碎石治疗胆结石、肾结石等;利用“B超”探察人体内病变.
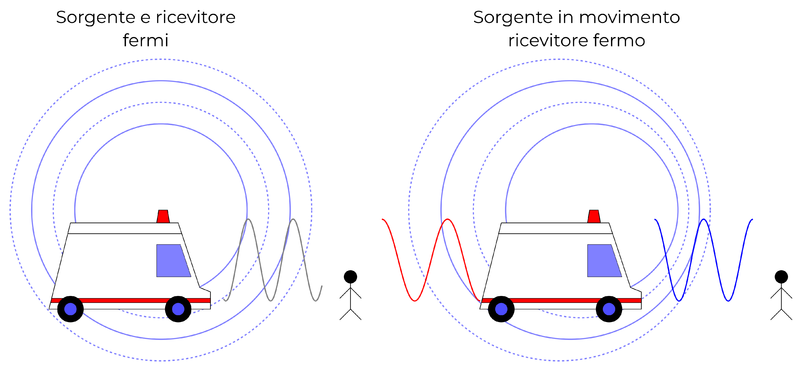
13.多普勒效应:
由于波源和观察者之间有相对运动使观察者感到频率发生变化的现象.其特点是:当波源与观察者有相对运动,两者相互接近时,观察者接收到的频率增大;两者相互远离时,观察者接收到的频率减小.