实验经典例题

【例1】（2021年高考全国甲卷第10题）某同学用图（a）所示电路探究小灯泡的伏安特性，所用器材有：
小灯泡（额定电压2.5V，额定电流0.3A）
电压表（量程300mV，内阻300 $Ω$ ）
电流表（量程300mA，内阻0.27 $Ω$ ）
定值电阻R₀
滑动变阻器R₁（阻值0-20 $Ω$ ）
电阻箱R₂（最大阻值9999.9 $Ω$ ）
电源E（电动势6V，内阻不计）
开关S、导线若干。
完成下列填空：

图（a）

（1）有3个阻值分别为10 $Ω$ 、20 $Ω$ 、30 $Ω$ 的定值电阻可供选择，为了描绘小灯泡电流在0~300mA的U–I曲线，R₀应选取阻值为___________ $Ω$ 的定值电阻；
（2）闭合开关前，滑动变阻器的滑片应置于变阻器的___________（填“a ”或“b ”）端；
（3）在流过电流表的电流较小时，将电阻箱R₂的阻值置零，改变滑动变阻器滑片的位置，读取电压表和电流表的示数U、I，结果如图（b）所示。当流过电流表的电流为10mA时，小灯泡的电阻为___________ $Ω$ （保留1位有效数字）；

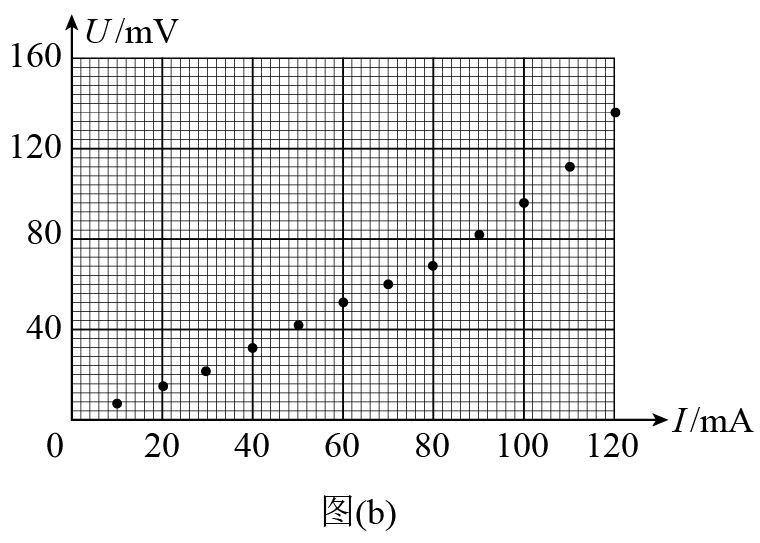
（4）为使得电压表满量程时对应于小灯泡两端的电压为3V，该同学经计算知，应将R₂的阻值调整为_______ $Ω$ 。然后调节滑动变阻器R₁，测得数据如下表所示：

U/mV	46.0	76.0	110.0	128.0	152.0	184.0	216.0	250.0
I/mA	160.0	180.0	200.0	220.0	240.0	260.0	280.0	300.0

（5）由图（b）和上表可知，随流过小灯泡电流的增加，其灯丝的电阻___________（填“增大”“减小”或“不变”）；
（6）该同学观测到小灯泡刚开始发光时流过电流表的电流为160mA，可得此时小灯泡电功率W₁=_______W（保留2位有效数字）；当流过电流表的电流为300mA时，小灯泡的电功率为W₂，则 $\frac{W_{2}}{W_{1}}$ =_______（保留至整数）。

展开答案

【答案】 (1). 10 (2). a (3). 0.7 (4). 2700 (5). 增大 (6). 0.074 (7). 10

【解析】（1）因为小灯泡额定电压2.5V，电动势6V，则滑动滑动变阻器时，为了保证电路安全，需要定值电阻分担的电压

$U = 6 V - 2.5 V = 3.5 V$

则有

$R_{0} = \frac{3.5 V}{0.3 V} \approx 11.7 Ω$

则需要描绘小灯泡在0~300mA的伏安特性曲线，即R₀应选取阻值为10 $Ω$ ；

（2）这是一个非常容易犯错的地方，要看清结构，为了保护电路，滑动变阻器的滑片应置于变阻器的a 端，这样上半部分的电压会小。

（3）由图可知当流过电流表的电流为10mA时，电压为7mV，则小灯泡的电阻为

$R = \frac{7 \times 10^{- 3}}{10 \times 10^{- 3}} = 0.7 Ω$

（4）由题知电压表满量程时对应于小灯泡两端的电压为3V时，有

$\frac{3}{R_{2} + R_{V}} = \frac{0.3}{R_{V}}$

解得 $R_{2} = 2700 Ω$

（5）由图（b）和表格可知流过小灯泡电流增加，图像中 $\frac{U}{I}$ 变大，则灯丝的电阻增大；

（6）根据表格可知当电流为160mA时，电压表的示数为46mA，根据（4）的分析可知此时小灯泡两端电压为0.46A，则此时小灯泡电功率

$W_{1} = 0.46 V \times 0.16 A \approx 0.074 W$

（7）同理可知当流过电流表的电流为300mA时，小灯泡两端电压为2.5V，此时小灯泡电功率

$W_{2} = 2.5 V \times 0.3 A = 0.75 W$

故有

$\frac{W_{2}}{W_{1}} = \frac{0.75}{0.074} = 10$

例题2（计算力）

（2021年高考全国乙卷物理第10题）一实验小组利用图（a）所示的电路测量一电池的电动势E（约1.5V）和内阻r（小于2 $Ω$ ）。图中电压表量程为1V，内阻 $R_{V} = 380.0 Ω$ ：定值电阻 $R_{0} = 20 .0 Ω$ ；电阻箱R，最大阻值为 $999.9 Ω$ ；S为开关。按电路图连接电路。完成下列填空：

图（a）

（1）为保护电压表，闭合开关前，电阻箱接入电路的电阻值可以选___________ $Ω$ （填“5.0”或“15.0”）；

（2）闭合开关，多次调节电阻箱，记录下阻值R和电压表的相应读数U；

（3）根据图（a）所示电路，用R、R₀、R_V、E 和r 表示 $\frac{1}{U}$ ，得 $\frac{1}{U}$ ___________；

（4）利用测量数据，做 $U - \frac{1}{U}$ 图线，如图（b）所示：

图（b）

（5）通过图（b）可得E___________V（保留2位小数），r___________ $Ω$ （保留1位小数）；

（6）若将图（a）中的电压表当成理想电表，得到的电源电动势为E’，由此产生的误差为

$∣ \frac{E^{'} - E}{E} ∣ \times 100 %$ ________

展开答案

【答案】 (1). 15.0 (2). $\frac{1}{U} = \frac{R_{V} + R_{0}}{E R_{V} R_{0}} R + \frac{1}{E} + \frac{R_{V} + R_{0}}{E R_{V} R_{0}} r$ (3). 1.55 (4). 1.0 (5). 5

【解析】（1）为了避免电压表被烧坏，接通电路时电压表两端的电压不能比电表满偏电压大，则由并联电路分压可得

$\frac{U}{\frac{R_{V} R_{0}}{R_{V} + R_{0}}} = \frac{E - U}{R + r}$

代入数据解得 $R = 7.5 Ω$ 因此选 $15 Ω$ 。

（3）由闭合回路的欧姆定律可得

$E = U + \frac{U}{\frac{R_{V} R_{0}}{R_{V} + R_{0}} (R + r)}$

化简可得

$\frac{1}{U} = \frac{R_{V} + R_{0}}{E R_{V} R_{0}} R + \frac{1}{E} + \frac{R_{V} + R_{0}}{E R_{V} R_{0}} r$

（5）[3][4]由上面公式可得

$\frac{R_{V} + R_{0}}{E R_{V} R_{0}} = k = \frac{1}{19 E}$

$\frac{1}{E} + \frac{R_{V} + R_{0}}{E R_{V} R_{0}} r = b = \frac{1}{E} + \frac{r}{19 E}$

由 $\frac{1}{U} - R$ 图象计算可得

选取两点求出斜率

$k = 0.034 V^{- 1} \cdot Ω$ , $b = 0.068 V^{- 1}$

代入可得 $E \approx 1.55 V$ , $r = 1.0 Ω$ 。

难点在于一是计算力大、二是选择不同的点计算结果会不一样，选择两个看上去最接近焦点的点，反而计算出0.032，图中的两点与标准答案一致，但是p2明显不在焦点，这种方式出题简直是毒害青年朋友，这也难怪很多优秀的人被埋没，都被培养成僵化的做题机器，本不想吐槽，这种出题思路不是在培养思维，想象力，熟练的应用方法，是彻底的傻逼行为，为了难为人而难为人，就好像再问你知道茴字有几种写法。好在后面的计算不需要这步的计算结果，实验题很多时候，相关新没那么大，如果计算不出果断放弃，继续做下面的分析。

（6）[5]如果电压表为理想电压表，则可有

$\frac{1}{U} = \frac{1}{E} + \frac{r}{E R_{0}} + \frac{1}{E R_{0}} R$

则此时

$E^{'} = \frac{1}{20 k}$

因此误差为

$η =∣ \frac{\frac{1}{20 k} - \frac{1}{19 k}}{\frac{1}{19 k}} ∣ \times 100 % = 5 %$

例题3

（新高考全国卷Ⅱ·浙江·第19题）小李在实验室测量一电阻R的阻值。
（1）因电表内阻未知，用如图1所示的电路来判定电流表该内接还是外接。正确连线后，合上开关S，将滑动变阻器的滑片P移至合适位置。单刀双掷开关K掷到1，电压表的读数 $U_{1} = 1.65 V$ ，电流表的示数如图2所示，其读数 $I_{1}$ ___________A；将K掷到2，电压表和电流表的读数分别为 $U_{2} = 1.75 V$ ， $I_{1} = 0.33 A$ 。由此可知应采用电流表___________（填“内”或“外”）接法。

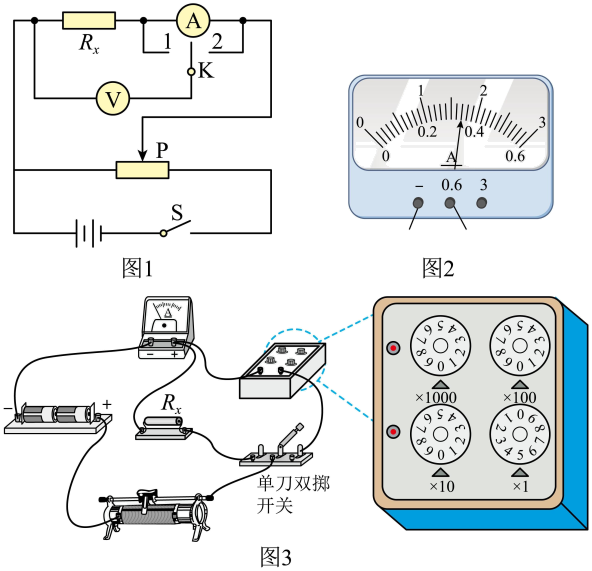
（2）完成上述实验后，小李进一步尝试用其它方法进行实验：

①器材与连线如图3所示，请在虚线框中画出对应的电路图___________；

②先将单刀双掷开关掷到左边，记录电流表读数，再将单刀双掷开关挪到右边，调节电阻箱的阻值，使电流表的读数与前一次尽量相同，电阻箱的示数如图3所示。则待测电阻 $R_{X} =$ ___________ $Ω$ 。此方法___________（填“有”或“无”）明显的实验误差，其理由是___________。

展开答案

【答案】 (1). 0.34 (2). 见解析 (3). 外 (4). 5 (5). 有 (6). 电阻箱的最小分度与待测电阻比较接近（或其它合理解释）

【解析】（1）由电流表的表盘可知电流大小为0.34A

（2）电路图

（3）

电压表的百分比变化为 $η_{1} = \frac{1.75 - 1.65}{1.75}$ =5.7%

电流表的百分比变化为 $η_{2} = \frac{0.34 - 0.33}{0.33}$ =3.0%

因此可知电压表的示数变化更明显，说明电流表的分压更严重，因此不能让电流表分压，采用外接法。

（4）.两次实验中电路电流相同，因此可有

$I = \frac{E}{R_{A} + r + R_{X}} = \frac{E}{R_{A} + r + R_{0}}$

可得 $R_{0} = R_{X}$

读数可得 $R_{X} = 5 Ω$

（5）.有

（6）电阻箱的最小分度和待测阻值阻值接近，这样测得的阻值不够精确，如待测电阻阻值为5.4Ω，则实验只能测得其为 $R_{X} = 5 Ω$ ，误差较大

例题4（电动势）

（新高考全国卷Ⅱ·湖南·第12题）某实验小组需测定电池的电动势和内阻，器材有：一节待测电池、一个单刀双掷开关、一个定值电阻（阻值为 $R_{0}$ ）、一个电流表（内阻为 $R_{A}$ ）、一根均匀电阻丝（电阻丝总阻值大于 $R_{0}$ ，并配有可在电阻丝上移动的金属夹）、导线若干。由于缺少刻度尺，无法测量电阻丝长度，但发现桌上有一个圆形时钟表盘。某同学提出将电阻丝绕在该表盘上，利用圆心角来表示接入电路的电阻丝长度。主要实验步骤如下：

（1）将器材如图（a）连接：

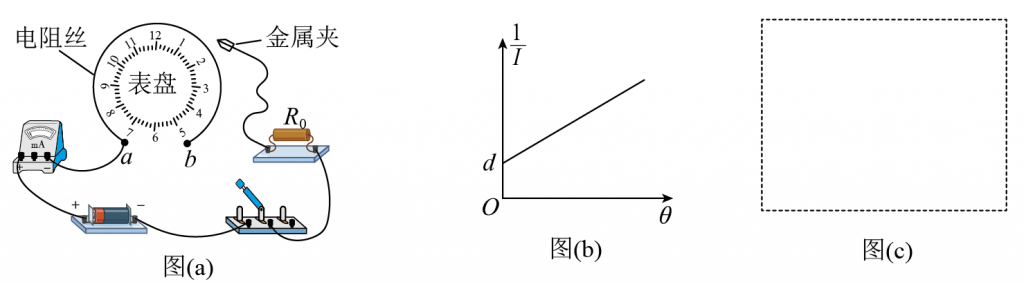
（2）开关闭合前，金属夹应夹在电阻丝的___________端（填“a”或“b”）；

（3）改变金属夹的位置，闭合开关，记录每次接入电路的电阻丝对应的圆心角 $Θ$ 和电流表示数 $I$ ，得到多组数据；

（4）整理数据并在坐标纸上描点绘图，所得图像如图（b）所示，图线斜率为 $k$ ，与纵轴截距为 $d$ ，设单位角度对应电阻丝的阻值为 $r_{0}$ ，该电池电动势和内阻可表示为 $E =$ ___________， $r =$ ___________（用 $R_{0}$ 、 $R_{A}$ 、 $k$ 、 $d$ 、 $r_{0}$ 表示）

（5）为进一步确定结果，还需要测量单位角度对应电阻丝的阻值 $r_{0}$ 。利用现有器材设计实验，在图（c）方框中画出实验电路图__________（电阻丝用滑动变阻器符号表示）；

（6）利用测出的 $r_{0}$ ，可得该电池的电动势和内阻。

展开答案

(1). $b$ (2). $\frac{r_{0}}{k}$ (3). $\frac{r_{0} d}{k} - R_{0} - R_{A}$

(4).

【解析】（2）[1]开关闭合前，为了保护电路中的元件，应将电阻丝的最大阻值接入电路，根据电阻定律 $R = ρ \frac{L}{S}$ 可知电阻丝接入越长，接入电阻越大，金属夹应夹在电阻丝的 $b$ 端。

（4）[2]设圆心角为 $θ$ 时，电阻丝接入电路中的电阻为 $θ r_{0}$ ，根据闭合电路欧姆定律 $E = U + I r$ 可知

$E = I (R_{A} + R_{0} + θ r_{0}) + I r$

整理得

$\frac{1}{I} = \frac{r_{0}}{E} θ + \frac{R_{A} + R_{0} + r}{E}$

结合图象的斜率和截距满足

$\frac{r_{0}}{E} = k$ , $\frac{R_{A} + R_{0} + r}{E} = d$

解得电源电动势和内阻为

$E = \frac{r_{0}}{k}$

$r = \frac{r_{0} d}{k} - R_{0} - R_{A}$

（5）[3]实验器材中有定值电阻 $R_{0}$ 和单刀双掷开关，考虑使用等效法测量电阻丝电阻，如图

原理的简单说明：

① 将开关置于 $R_{0}$ 位置，读出电流表示数 $I_{0}$ ；

② 将开关置于电阻丝处，调节电阻丝的角度，直到电流表示数为 $I_{0}$ ，读出此时角度θ ；

③ 此时 $θ r_{0} = R_{0}$ ，即可求得 $R_{0}$ 的数值。

例题5多（电表改装）

(2021·四川绵阳市第二次诊断)将一微安表先改装成量程1 mA的电流表，再改装成量程5 V的电压表，并与标准电压表对比校准。图1甲是改装后电压表与标准电压表对比校准的电路图，虚线框中是改装后电压表电路，V₀是量程6 V的标准电压表。已知微安表满偏电流为250 μA，标记的内阻为600 Ω，电阻箱R₁、R₂调节范围为0～9 999.99 Ω。

(1)微安表改装。图甲中电阻箱的阻值分别调节到R₁＝________ Ω，R₂＝________ Ω。

(2)实物连线。选用合适的器材，按照图甲正确连接电路。

(3)对比校准。正确连接电路后，闭合开关，调节滑动变阻器，当标准电压表的示数如图乙所示时，微安表(改装后电压表)的示数如图丙所示，由此可以推测出改装电压表量程的真实值________5 V(选填“大于”或“小于”)。

(4)重新调整。通过检测发现：电阻箱R₁、R₂阻值是准确的，而微安表标记的内阻不准确，这是改装电压表量程的真实值不是5 V的原因。再通过调节电阻箱R₁、R₂的阻值，使改装电压表量程的真实值为5 V，以下调节方案可行的有________(填序号)。

A.保持R₁不变，将R₂增大到合适值

B.保持R₁不变，将R₂减小到合适值

C.保持R₂不变，将R₁增大到合适值

D.保持R₂不变，将R₁减小到合适值

展开答案

【答案】　(1)200　4 850　(3)小于　(4)AD

【解析】　(1)微安表并联电阻改装为1 mA的电流表，有 $I_{g} R_{g} ＝ (I － I_{g}) R_{1}$
即 $250 \times 10^{- 6} \times 600 ＝ (1 \times 10^{- 3} － 250 \times 10^{- 6}) R_{1}$
解得 $R_{1} ＝ 200 Ω$ .

改装后的电流表满偏电流为1 $m A$ ，再改装为5 V的电压表，总电阻应该是 $R = \frac{5 V}{10^{- 3} A} = 5000 Ω$ 内阻为 $R_{A} = \frac{R_{1} R_{g}}{R_{1} + R_{g}} = 150 Ω$ 串联电阻R₂， $R_{A} + R_{2} = 5000 Ω$ ，解得 $R_{2} ＝ 4850 Ω$ 。

(3)标准电压表的精度为 $0.2 V$ ，指针对应的真实电压为 $3.2 V$ ；微安表的精度为 $5 μ A$ ，读数为 $170 μ A$ ，从读数的比例可以看出偏小。

根据偏角和电压成正比有 $\frac{3.2}{170} = \frac{U}{250}$ ，解得 $U \approx 4.71 V < 5 V$ ，即改装电压表量程的真实值小于5 V。

(4)因电压表的量程偏小，改装关系为 $U ＝ I (R_{A} ＋ R_{2}), I_{g} R_{g} ＝ (I － I_{g}) R_{1}$ ，则保持 $R_{1}$ 不变，即保持 $I$ 不变，可将 $R_{2}$ 增大到合适值，从而使 $U$ 增大；另保持 $R_{2}$ 不变，将 $R_{1}$ 减小到合适值，即将I变大，也能使 $U$ 增大，故选A、D。

例题6（电动势内阻）

(2021·安徽淮北市高三一模)某同学用图甲所示电路测量电池的电动势和内阻以及一个未知电阻 $R_{1}$

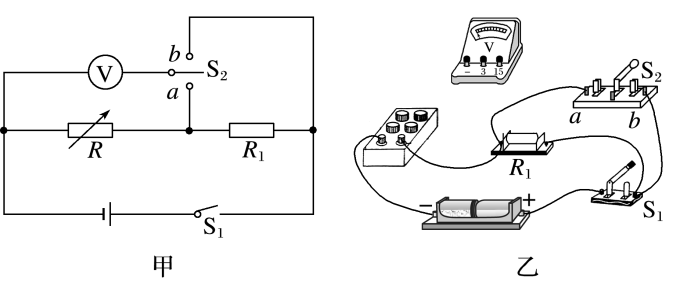
(1)请用笔画线代替导线完成图乙实物图连接；

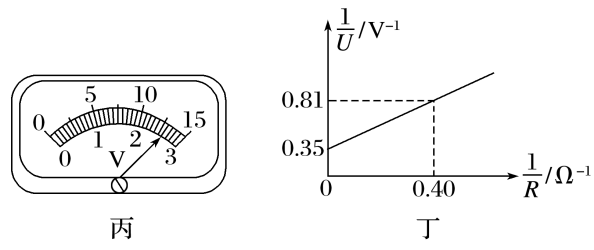
(2)将 $S_{2}$ 接到a，闭合 $S_{1}$ ，拨动电阻箱旋钮，使电阻箱阻值为 $11.0 Ω$ ，此时电压表(内阻很大)读数为 $2.20 V$ ；然后保持电阻箱示数不变，将 $S_{2}$ 切换到 $b$ ，闭合 $S_{1}$ ，电压表读数如图丙所示，则其读数为________ $V$ ，此可算出电阻 $R_{1}$ 的阻值为________ $Ω$ (结果保留三位有效数字)；

(3)在完成上述操作后，该同学将 $S_{2}$ 切换到 $a$ ，闭合 $S_{1}$ ，多次调节电阻箱，读出多组电阻箱的示数R和对应的电压表示数U，由测得的数据，绘出了如图丁所示的 $\frac{1}{U} - \frac{1}{R}$ 图线，由此可求得电源电动势 $E$ ＝________ $V$ ，电源内阻 $r$ ＝________ $Ω$

展开答案

【答案】　(1)见解析图　(2)2.60　2.00　(3)2.86　1.29

【解析】　(1)题图甲中电源是两节电池串联，所以电压表选3 V量程，根据原理图连接实物图如下

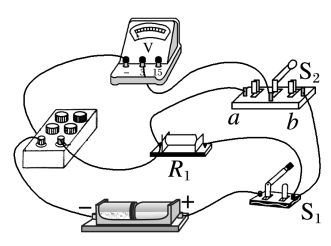
(2)题图丙电压表量程是 $3 V$ ，精确度为 $0.1 V$ ，故其读数为 $2.60 V$ ；

电路中的电流为 $I ＝ \frac{U_{R}}{R} ＝ \frac{2.20}{11.0} A ＝ 0.20 A$

电阻R₁的阻值为

$R_{1} ＝ \frac{U - U_{R}}{I} = \frac{2.60 - 2.20}{0.20} Ω = 2 Ω$

由闭合电路欧姆定律可得 $E ＝ U + \frac{U}{R} (R_{1} + r)$
则可得 $\frac{1}{U} = \frac{1}{E} + \frac{R_{1} + r}{E} \times \frac{1}{R}$

可知，题图丁图线的截距为电动势的倒数，则可得 $E = \frac{1}{0.35} V \approx 2.86 V$

图线斜率为 $\frac{R_{1} + r}{E} = \frac{0.81 - 0.35}{0.4}$

则可得 $r = \frac{0.81 - 0.35}{0.4} \times 2.86 Ω - 2 Ω \approx 1.29 Ω$

例题7（中值电阻）

图甲为一个简单的多用电表的电路图，其中电源的电动势E＝1.5 V、内阻r＝1.0 Ω，电流表内阻R_g＝10 Ω、满偏电流I_g＝100 mA。该多用电表表盘如图乙所示，下排刻度均匀，C为上排刻度线的中间刻度。

(1)选择开关接“1”，指针指在图乙所示位置时示数为________ mA。

(2)如果选择开关接“3”，此状态下多用电表为量程50 V的电压表，图甲中电阻R₂＝________ Ω。

(3)如果选择开关接“2”，该多用电表可用来测电阻，C刻度应标为________ Ω。

(4)如果选择开关接“2”，将该多用电表的电池换成一个电动势为1.5 V、内阻为12 Ω的电池，正确调零后测量某电阻的阻值，其测量结果________(选填“偏大”“偏小”或“准确”)。

(5)如果选择开关接“2”，可以采用变换电源的方式将倍率调为×10挡，且能够正常进行欧姆调零，则需新电源的电动势应为E₂＝________ V。

展开答案

【答案】　(1)71　(2)490　(3)15 $Ω$ 　(4)准确　(5)15 $V$

【解析】　(1)选择开关接“1”时测电流，电表表盘下面刻度的最小分度值为2 mA，指针在两最小刻度之间进行估读，故其示数为71 mA。

(2)根据串联电路有分压作用可知，当电表满偏时有

U＝I_g(R_g＋R₂)

所以开关接“3”时R₂＝490 $Ω$ 。

(3)欧姆表的内阻R_内＝ $\frac{E}{I_{g}}$ ＝15 $Ω$ ，由于欧姆表的中值电阻等于欧姆表内阻，故C处刻度为15 $Ω$ 。

(4)准确，因为电源内阻的变化，可以通过调零电阻阻值的变化来抵消，所以调零后测量某电阻阻值的测量结果是准确的。

(5)×10挡中值电阻为150 Ω，根据闭合电路欧姆定律有E＝I_gR_内得E＝15 V。

例题8（测量电阻）

（2021·湘豫名校4月联考） 某同学欲测量一阻值大约为10 Ω，粗细均匀的金属线的电阻率。实验桌上除游标卡尺、螺旋测微器、导线和开关外，还有以下器材可供选择：

A.电源E（电动势为6.0 V）

B.电压表V（量程为0～6 V，内阻约为8 kΩ）

C.电流表A₁（量程为0～0.6 A，内阻约为0.2 Ω）

D.电流表A₂（量程3 A，内阻约0.05 Ω）

E.滑动变阻器R₂（最大阻值5 Ω，额定电流2 A）

（1）用游标卡尺测得该材料的长度L如图甲所示，读数L＝________mm；用螺旋测微器测得该材料的直径D如图乙所示，读数D＝________mm。

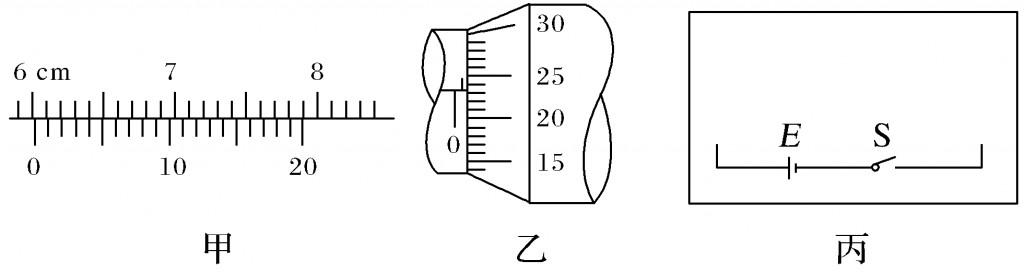
（2）测量导电材料的电阻时，为了便于调节，测量尽可能地准确，实验中所用电流表应选用________（填所选仪器前的字母符号），选择合适的实验器材，在图丙方框内把实验原理图补充完成，把器材符号标在电路图上。

（3）设测得导电材料的电阻为R，导电材料的长度为L，导电材料的直径为D，求得导电材料的电阻率为________（用R、L、D三个物理量表述）。

（4）为了验证实验数据，实验小组决定用欧姆表测一下电阻，使用步凑，调节调节____，使电表表针停在____（填“电阻”或“电流”）的0刻度线，然后将黑表笔分别插入“-”“+”插口，并将两笔短接，调节________。使电表表针停在____（填“电阻”或“电流”）。

展开答案

【答案】　（1）60.20　0.732　（2）C　见解析　（3） $\frac{π D^{2}}{4 L} R$ （4）指针定位螺丝电流欧姆调零旋钮电阻

【解析】

（1）游标卡尺的读数为60 mm＋4×0.05 mm＝60.20 mm

根据螺旋测微器读数规则可得d＝0.5 mm＋0.232 mm＝0.732 mm。

（2）待测电阻的最大电流 $I_{m a x} = \frac{U}{R} = 0.6 A$ ，因此电流表选A₁，滑动变阻器阻值较小，用分压式接法，待测电阻远小于电压表内阻，属于小电阻，电流表采用外接法，电路图如图所示。

（3）根据电阻定律 $R = \frac{L}{ρ \frac{1}{4} π D^{2}}$ (，解得 $ρ = \frac{π D^{2} R}{4 L}$

例题9

如图为某同学组装完成的简易多用电表的电路图。图中 $E$ 是电池； $R_{1}$ 、 $R_{2}$ 、 $R_{3}$ 、 $R_{4}$ 和 $R_{5}$ 是固定电阻， $R_{6}$ 是可变电阻；虚线方框内为换挡开关， $A$ 端和 $B$ 端分别与两表笔相连。该多用电表有 $5$ 个挡位， $5$ 个挡位分别为直流电压 $1 V$ 挡和 $5 V$ 挡。直流电流 $1 m A$ 和 $2.5 m A$ 挡，欧姆 $\times 100 Ω$ 挡。

（1）测量时，接线柱 $B$ 接的是______（填“红”或“黑”）表笔；若开关 $B$ 端是与“ $1$ ”相连的，则此时多用电表的挡位为______挡；（填题干中所给 $5$ 个挡位中的一个）

（2）电路中 $R_{4}$ 与 $R_{5}$ 的比值______（填“大于”“小于”或“等于”） $\frac{1}{4}$ ；

（3）若电池 $E$ 的电动势为 $1.5 V$ ，当把开关 $B$ 端接到位置 $3$ ，短接 $A$ 、 $B$ 表笔进行欧姆调零后，用该挡测量一个未知电阻阻值，指针偏转到电流表 $G$ 满偏刻度的 $\frac{3}{4}$ 处，则该电阻的阻值为______ $Ω$ 。电池 $E$ 使用时间较长，电池的电动势变小、内阻变大；重新调零后，实验要求若被测电阻阻值等于中值电阻时，测量的相对误差 $\frac{| R_{测} - R_{真} |}{R_{真}} \times 100 %$ 不能超过 $\pm 5 %$ ，则电池电动势降低为______（结果保留两位有效数字）时必须更换电池；

（4）另一个同学设计了一只简易欧姆表，并将表盘的电流刻度转化为电阻刻度；其电路如下图所示。关于该欧姆表，下列说法正确的是______。

A、电阻刻度的零位在表盘的左端

B、表盘上的电阻刻度是均匀的

C、测量前，需要红、黑表笔短接调零

D、测量后，应将开关 $S$ 断开

展开答案

【】

解析 (1) [1]根据欧姆表原理可知，黑笔接电源正极，红笔接电源负极，所以与 $B$ 接线柱相连的是红表笔； [2]若开关 $B$ 端是与“ $1$ ”相连的，则此时应为量程较大的电流表，所以多用电表的挡位为 $2.5 mA$ ；

(2) [3]当开关接 $4$ 时，多用电表的量程为 $1 V$ 的电压表，有 $1 V = 1 mA \cdot R_{4} + 1 mA \cdot R_{g}$ 当开关接 $5$ 时，多用电表的量程为 $5 V$ 的电压表，有 $5 V = 1 mA \cdot (R_{4} + R_{5}) + 1 mA \cdot R_{g}$

联立可得 $R_{4} < 1000 Ω, R_{5} = 4000 Ω$

所以 $\frac{R_{4}}{R_{5}} < \frac{1}{4}$

(3) [4]当把开关 $B$ 端接到位置 $3$ ，短接 $A$ 、 $B$ 表笔，有

$\begin{aligned} I & = 1 mA \\ E & = I R_{内} \end{aligned}$

用该挡测量一个未知电阻阻值，指针偏转到电流表 $G$ 满偏刻度的 $\frac{3}{4}$ 处，有

$E = \frac{3}{4} I (R_{内} + R_{x})$ 联立解得 $R_{x} = 500 Ω$

[5]当电动势变小，内阻变大时，重新进行欧姆调零，其满偏电流保持不变，根据闭合电路欧姆定律可得 $I = \frac{E}{R_{内} + R_{x}} = \frac{I_{g} R_{内}}{R_{内} + R_{x}}$

当待测电阻等于内阻时，即 $\begin{aligned} R_{测} & = 1500 Ω \\ \frac{| R_{测} - R_{内} |}{R_{内}} \times 100 % & = 5 % \end{aligned}$

解得 $R_{真} = 1429 Ω$

此时 $\begin{aligned} R_{内}^{'} & = 1429 Ω \\ \frac{1}{2} I_{g} & = \frac{E^{'}}{2 R^{'}} \end{aligned}$ 解得 $E^{'} = 1.4 V$

(4) [6]A、C项，当红黑表笔短接时，电流表被短路，电流为零，所以电阻刻度的零位在表盘的左端，所以测量前不需要红、黑表笔短接调零，故A正确，C错误；

B、根据闭合电路欧姆定律可得 $E = (I + \frac{I R_{G}}{R_{x}}) (r + R + \frac{R_{G} R_{x}}{R_{G} + R_{x}})$ 所以 $I = \frac{E}{(1 + \frac{R_{G}}{R_{x}}) (r + R + \frac{R_{G} R_{x}}{R_{G} + R_{x}})}$ 由此可知 $I - R_{x}$ 为非线性关系，

所以表盘上的电阻刻度是不均匀的，故B错误； D、测量后，应将开关 $S$ 断开，使得电路处于断路状态，故D正确。

故选：A、D。

电学实验创新

Previous Topic

Back to Lesson

Next Topic