曲线运动
如图所示,固定半圆弧容器开口向上,AOB是水平直径,圆弧半径为R,在A、B两点,分别沿AO、BO方向同时水平抛出一个小球,结果两球落在了圆弧上的同一点,从A点抛出的小球初速度是从B点抛出小球初速度的3倍,不计空气阻力,重力加速度为g,则)( )
A.从B点抛出的小球先落到圆弧面上
B.从B点抛出的小球做平抛运动的时间为$\sqrt{\dfrac{\sqrt{3}R}{g}}$
C.从A点抛出的小球初速度大小为$\dfrac{\sqrt{3\sqrt{3}gR}}{2}$
D.从A点抛出的小球落到圆弧面上时,速度的反向延长线过圆心O
展开答案
【答案】BC
【解析】A.由于两球落在圆弧上的同一点,因此两球做平抛运动下落的高度相同,运动的时间相同,由于同时抛出,因此一定同时落到圆弧面上,A错误;
B.由水平方向的位移关系可知,由于A点处抛出的小球初速度是B点处抛出小球的3倍,因此A点处抛出小球运动的水平位移是B点处抛出小球运动的水平位移的3倍,由于$X_A+X_B=2R$,因此B点处小球运动的水平位移$X_B=\dfrac{1}{2}R$,根据几何关系可知,两球做平抛运动下落的高度为$\dfrac{\sqrt{3}}{2}$,运动的时间$t=\sqrt{\dfrac{2h}{g}}=\sqrt{\dfrac{\sqrt{3}R}{g}}$,B正确;
C.A点抛出的小球初速度$V_A=\dfrac{\dfrac{3}{2}R}{\sqrt{\dfrac{\sqrt{3}R}{g}}}=\dfrac{\sqrt{3\sqrt{3}gR}}{2}$,C正确;
D.由于O点不在A点抛出小球做平抛运动的水平位移的中点,D错误.
(2018·全国卷Ⅲ·17)在一斜面顶端,将甲、乙两个小球分别以$v$和$\dfrac{v}{2}$的速度沿同一方向水平抛出,两球都落在该斜面上。甲球落至斜面时的速率是乙球落至斜面时速率的( )
A.2倍 B.4倍 C.6倍 D.8倍
展开答案
【答案】 A
【解析】 如图所示,可知
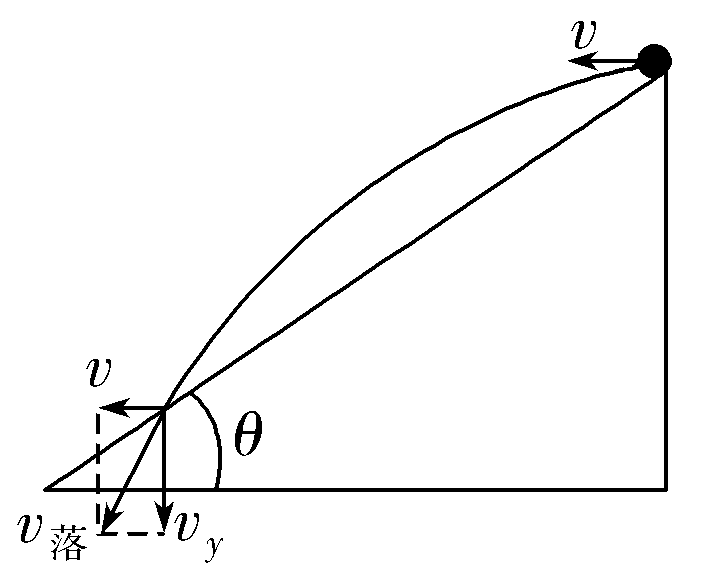
$x=vt$
$tan \theta=\dfrac{y}{x}=\dfrac{\dfrac{1}{2}gt^2}{vt}=\dfrac{gt}{2v}$
则$v_y=gt=2vtan \theta $
则落至斜面的速率$v_落=\sqrt{v^2+v_y^2}=v\sqrt{1+4tan^2\theta}$,即v落∝v,甲、乙两球抛出速度为v和$\dfrac{v}{2}$,则可得落至斜面时速率之比为2∶1。
拓展:
(多选)如图所示,倾角为θ的斜面上有A、B、C三点,现从这三点分别以不同的初速度水平抛出一小球,三个小球均落在斜面上的D点,今测得AB:BC:CD=5:3:1,由此可判断(不计空气阻力)( )
A. 图中三小球比较,从A处抛出的小球飞行过程速度变化最快
B. A、B、C处三个小球落在斜面上时速度与初速度间的夹角之比为1:1:1
C. A、B、C处三个小球的初速度大小之比为3:2:1
D. A、B、C处三个小球的运动轨迹可能在空中相交
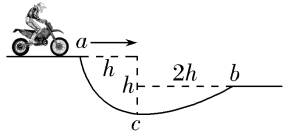
(2020·全国卷Ⅱ,16)如图,在摩托车越野赛途中的水平路段前方有一个坑,该坑沿摩托车前进方向的水平宽度为3h,其左边缘a点比右边缘b点高0.5h。若摩托车经过a点时的动能为E1,它会落到坑内c点,c与a的水平距离和高度差均为h;若经过a点时的动能为E2,该摩托车恰能越过坑到达b点。$\dfrac{E_2}{E_1}$等于( )
展开答案
【答案】 B
【解析】 摩托车落到c点时,根据平抛运动规律有$h=v_1t_1$,$2h=\dfrac{1}{2}gt_1^2$,解得$v_1^2=\dfrac{gh}{2}$;同理摩托车落到b点时有$v_2^2=9gh$。又动能$E_1=\dfrac{1}{2}mv_1^2$、$E_2=\dfrac{1}{2}mv_2^2$,所以$\dfrac{E_2}{E_1}=18$,故A、C、D项错误,B项正确。
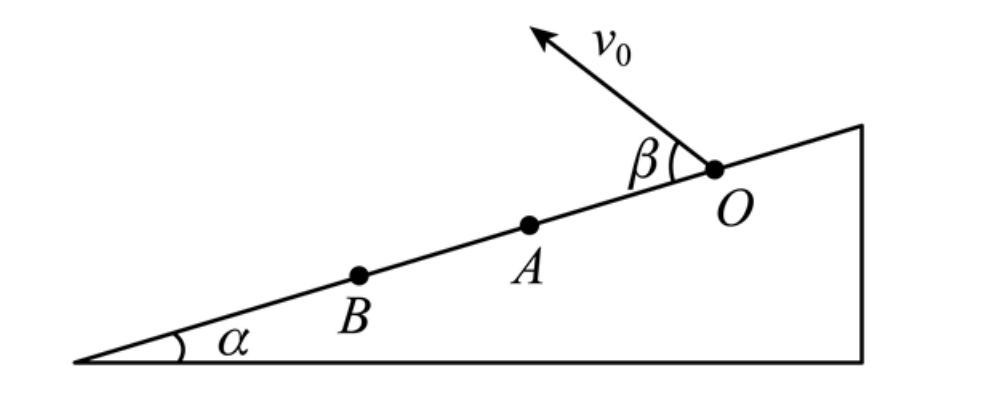
(2023·江苏南京·统考二模)如图所示,倾角为$a$的足够长斜面,现从斜面上 O点与斜面成$\beta$ 角($\beta <90°$),以速度 $v_0$ 、$2v_0$分别抛出小球 P、Q,小球 P、Q 刚要落在斜 面上 A、B 两点时的速度分别 $v_P$ 、 $v_Q$,设 O、A 间的距离为 $S_1$,O、B 间的距离为$S_2$, 不计空气阻力,当$\beta$取不同值时下列说法正确的是( )
A.$v_Q$ 一定等于 $2v_p$
B.$v_Q$ 方向与斜面的夹角一定小于$v_P$ 方向与斜面的夹角
C.P、Q 在空中飞行的时间可能相等
D.$s_2$ 可能大于$4s_1$
展开答案
【答案】 A
【解析】 我们只需要沿OA斜面进行速度分解,那么加速度就是$a_y= gcosa$ 这样就会大大简化分解方式, 相当与垂直于斜面做一个类竖直上抛运动,那么时间$t_Q=\dfrac{2v_{0y}}{a_y}$,$t_P=\dfrac{v_{0y}}{a_y}$. 所以飞行时间比就是2:1
也就是说以斜面对称,落地速度就等于初速度,所以速度就是2:1
也可以正常理解水平速度不变,因为斜面是同一个,那么实际速度和水平速度的比例应该一样,水平速度的比值是2:1,那么实际速度也应该一样。
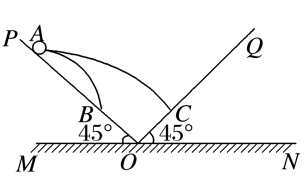
(多选)如图所示,固定斜面PO、QO与水平面MN的夹角均为45°,现由A点分别以$v_1$、$v_2$先后沿水平方向抛出两个小球(可视为质点),不计空气阻力,其中以$v_1$抛出的小球恰能垂直于QO落于C点,飞行时间为t,以v2抛出的小球落在PO斜面上的B点,且B、C在同一水平面上,重力加速度大小为g,则( )
A.落于B点的小球飞行时间为t
B.$v_2=gt$
C.落于C点的小球的水平位移为$gt^2$
D.A点距水平面MN的高度为$\dfrac{3}{4}gt^2$
展开答案
【答案】 ACD
【解析】 落于C点的小球速度垂直QO,分解速度如图所示,
则$V_1=gt$,水平位移$x=v_1=gt^2$,选项C正确;落于B点的小球,因B、C在同一水平面上,下落高度相同,故飞行时间也为t,有$tan45=\dfrac{\dfrac{1}{2}gt^2}{v_2t}=\dfrac{gt}{2v_2}$,$v_2=\dfrac{gt}{2}$,选项A正确,B错误;设C点距地面的高度为h,由几何关系知
$2h=v_1t-v_2t$,得$h=\dfrac{1}{4}gt^2$
故A点距水平面MN的高度$H=h+\dfrac{1}{2}gt^2=\dfrac{3}{4}gt^2$选项D正确.
如图所示,AC是倾角为30°的斜面,CD部分为水平面,小球从斜面顶端A点以初速度v0水平抛出,刚好落在斜面上的B点,AB=$\dfrac{1}{3}$AC,现将小球从斜面顶端A点以初速度2v0水平抛出,不计空气阻力,小球下落后均不弹起,重力加速度为g,则小球两次在空中运动过程中( )
A.时间之比为1∶2
B.时间之比为1:$\sqrt{3}$
C.水平位移之比为1: 9
D.当初速度为v0时,小球在空中离斜面的最远距离为$\dfrac{\sqrt{3}v_0^2}{12g}$
展开答案
【答案】BD
【答案】BD
【解析】AB.设小球的初速度为v0时,落在斜面上时所用时间为t,斜面长度为3L.小球落在斜面上时有
$tan \theta=\dfrac{\dfrac{1}{2}gt^2}{v_0t}=\dfrac{gt}{2v_0}$
解得
$t=\dfrac{2v_0 \cdot tan \theta}{g}$
设落点距斜面顶端距离为s,则有
$s=\dfrac{v_0t}{cos \theta}=\dfrac{2v_0^2tan \theta}{g cos \theta} \propto v_0^2$
若斜面足够长,两次小球均落在斜面上,落点距斜面顶端距离之比为1∶4,则第二次落在距斜面顶端4L处,大于斜面的长度,可知以2v0水平抛出时小球落在水平面上.两次下落高度之比为1∶3,根据
$h=\dfrac{1}{2}gt^2$
解得
$t=\sqrt{\dfrac{2h}{g}}$
所以时间之比为$1:\sqrt{3}$,故A错误,B正确;
图像法:这种方法超好,高中阶段用图像更容易理解!
C.根据
$x=v_0t$
可得水平位移之比为
$x_1:x_2=v_0t_1:2v_0t_2=1:2\sqrt{3}$
故C错误;
D.当小球的速度方向与斜面平行时,小球到斜面的距离最大.即在小球距离斜面最远时,垂直于斜面方向的速度等于零,建立沿斜面和垂直于斜面的平面直角坐标系,将初速度v0和重力加速度g进行分解,垂直于斜面的最远距离
$H=\dfrac{(v_0sin 30 °)^2}{2gcos 30 °}=\dfrac{\sqrt{3}v_0^2}{12g}$
故D正确。
(2020·辽宁瓦房店三中期中)如图所示,A、B两物体系在跨过光滑定滑轮的一根轻绳的两端,当A物体以速度v向左运动时,系A、B的绳分别与水平方向成α、β角,此时B物体的速度大小为( )
A.$\dfrac{v sin \alpha}{sin \beta}$ B.$\dfrac{v cos \alpha}{sin \beta}$ C.$\dfrac{v sin \alpha}{cos \beta}$ D.$\dfrac{v cos \alpha}{cos \beta}$
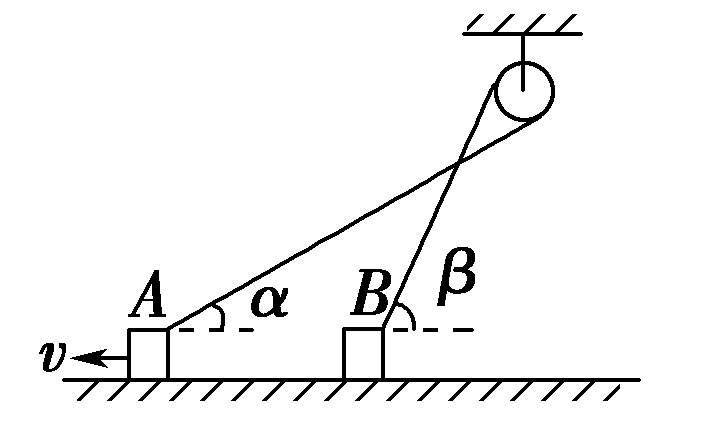
展开答案
【答案】D
【解析】将A物体的速度沿着绳子方向与垂直绳子方向进行分解,如图所示
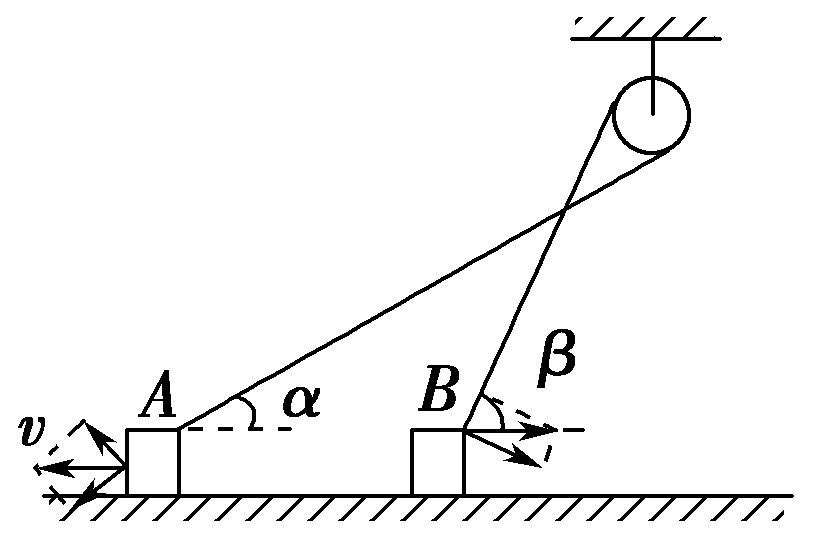
则A在沿绳方向的速度大小为$vcos \alpha$;将B物体的速度沿着绳子方向与垂直绳子方向进行分解,则B在沿着绳子方向的速度大小为$v_b cos \beta$,由于沿着绳子方向速度大小相等,所以有$vcos \alpha =v_Bcos \beta$,因此$v_B=\dfrac{v cos \alpha}{cos \beta}$,且方向向右,选项D正确。
如图所示为竖直黑板,下边为黑板的水平槽,现有一三角板ABC,∠C=30°。三角板上A处固定一大小不计的滑轮。现让三角板竖直紧靠黑板,BC边与黑板的水平槽重合,将一细线一端固定在黑板上与A等高的Q点,另一端系一粉笔头(可视为质点)。粉笔头最初与C重合,且细线绷紧。现用一水平向左的力推动三角板向左移动,保证粉笔头紧靠黑板的同时,紧靠三角板的AC边,当三角板向左移动的过程中,粉笔头会在黑板上留下一条印迹。关于此印迹,以下说法正确的是()
A.若匀速推动三角板,印迹为一条直线
B.若匀加速推动三角板,印迹为一条曲线
C.若变加速推动三角板,印迹为一条曲线
D.无论如何推动三角板,印迹均为直线,且印迹与AC边成75°角
展开答案
【答案】AD
解:ABC、若三角板向左移动的过程中,粉笔头会在黑板上留下的痕迹如图中CD轨迹,由于粉笔垂直于斜面向上运动,又小球相对于黑板水平方向向左运动,其运动轨迹为一条直线,故A正确,B、C错误;
日常生活中我们很容易被直觉欺骗,所以才需要画图验证。
D、根据图中的几何关系可得,∠ACD=∠ADC=180°−30°2=75°,故D正确。
故选AD。
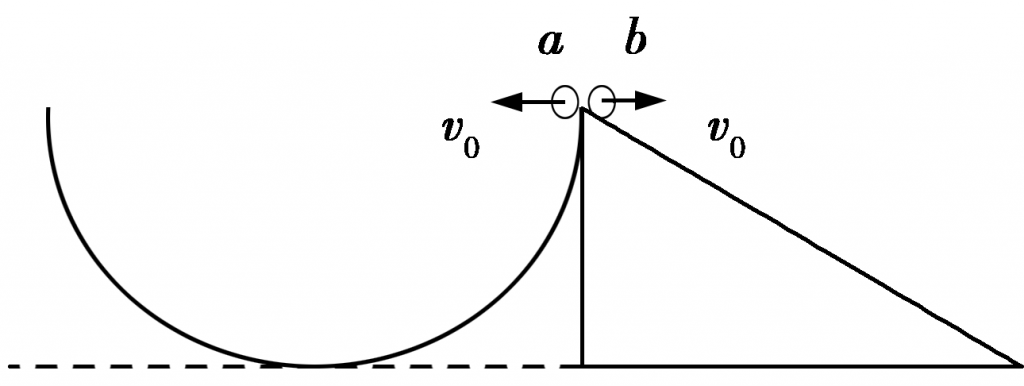
如图所示,a、b两小球分别从半圆轨道顶端和斜面顶端以大小相等的初速度v0同时水平拋出,已知半圆轨道的半径与斜面竖直高度相等,斜面底边长是其竖直高度的2倍,若小球a能落到半圆轨道上,小球b能落到斜面上,a、b均可视为质点,则( )
A.a球一定先落在半圆轨道上
B.b球一定先落在斜面上
C.a、b两球可能同时落在半圆轨道和斜面上
D.a球可能垂直落在半圆轨道上
展开答案
【答案】C
【解析】
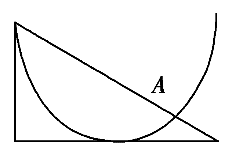
ABC.将半圆轨道和斜面轨道重叠一起,如图所示,可知若小球初速度合适,两小球可同时落在距离出发点高度相同的交点A处,改变初速度,可以落在半圆轨道,也可以落在斜面上,故AB错误,C正确;
D.若a小球垂直落在半圆轨道上,速度反向延长线必过水平位移中点,即圆心,那么水平位移就是直径,小球的水平位移一定小于直径,所以小球不可能垂直落在半圆轨道上,故D错误。
故选C。
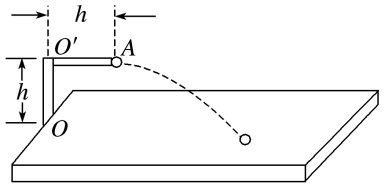
如图所示,乒乓球的发球器安装在足够大的水平桌面上,可绕竖直转轴OO′转动,发球器O′A部分水平且与桌面之间的距离为h,O′A部分的长度也为h,重力加速度为g。打开开关后,发球器可将乒乓球从A点以初速度v0水平发射出去,$\sqrt{2gh}$≤v0≤$2\sqrt{2gh}$ .设发射出去的所有乒乓球都能落到桌面上,乒乓球可视为质点,空气阻力不计。若使该发球器绕转轴OO′在90°的范围内来回缓慢地水平转动,持续发射足够长时间后,乒乓球第一次与桌面碰撞区域的面积S是( )
A.2πh2 B.3πh2 C.4πh2 D.8πh2
展开答案
【答案】C
【解析】设乒乓球做平抛运动的时间为t,则
$t=\sqrt{\dfrac{2h}{g}}$
当速度最大时,水平位移具有最大值
$x_{max}=v_{max}t=2\sqrt{2gh}\times \sqrt{\dfrac{2h}{g}}=4h$
当速度最小时,水平位移具有最小值
$x_{min}=v_{min}t=\sqrt{2gh}\times \sqrt{\dfrac{2h}{g}}=4h$
其中vmax、vmin为v0的最大值和最小值,又因为发球器O′A部分长度也为h,故乒乓球的落点距竖直转轴距离的范围为
3h≤x≤5h
乒乓球第一次与桌面碰撞区域是一个圆心角为90°的宽度为2h的环形带状区域,其面积为
$S=\dfrac{1}{4} \times \pi [(5h)^2-(3h)^2]=4 \pi h^2$
故选C。
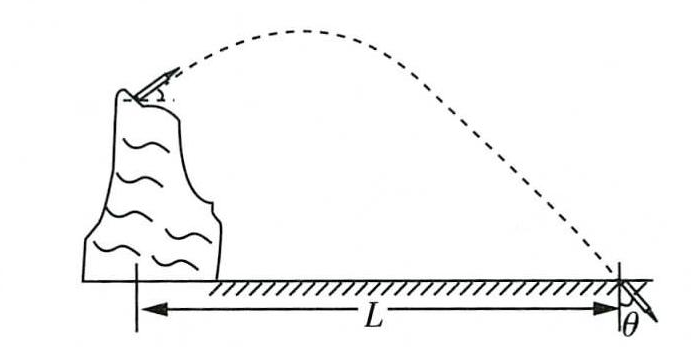
在某次军事演习中,某小队奉命在山上用小型迫击炮对某阵地进行打击,如图所示,发射位置与攻击阵地间的水平距离L=12 km。数字检测系统检测出炮弹打出时速度与水平方向的夹角$theta=37°$,击中目标时速度与竖直方向的夹角也为$theta=37°$,忽略炮弹飞行过程中受到的空气阻力,重力加速g=10m/s,sin37=0.6度为,则()
A:40 s.炮弹在空中飞行的时间为
B:3500 m.炮弹发射处与击中目标间的高度差为
C:16:9.炮弹发射速度与击中目标时的速度之比为
D.炮弹飞行过程中,单位时间内速度变化量的方向不断改变
展开答案
【答案】B
$\dfrac{v_0cos\theta}{tan\theta}=-v_0+gt$
$L=v_0 cos\theta t$
解得:
$v_0=300m/s$
$t=50s$
$H=-v_0sin\theta +\dfrac{1}{2}gt^2=3500m$
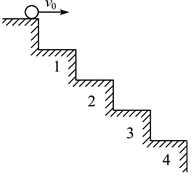
如图所示,小球从楼梯上以2m/s的速度水平抛出,所有台阶的高度和宽度均为30cm,g取10m/s2,小球抛出后首先落到的台阶是( )
A.1
B.2
C.3
D.4
展开答案
【答案】C
因为横着和竖着相等,所以才会
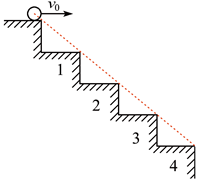
如图所示,设小球落在斜线上的时间为t,由位移公式可得
$x=v_0t$
$y=\dfrac{1}{2}gt^2$
由于所有台阶的高度和宽度均相等,故位移偏角为45°,即
$tan45=\dfrac{y}{x}$
联立解得t=0.4s,对应的水平位移为$x=0.8m$
每级台阶宽0.3m,故小球首先落到第3级台阶上,C正确。
将跳远运动员起跳落地的过程看成斜抛运动,若一运动员(可看做质点)跳远水平距离可达8.16m,最高可达2.04m,设他离开地面时的速度方向与水平面的夹角为α,不计空气阻力,则正切值$tana$等于( )
A、$\dfrac{1}{2}$
B、$\dfrac{3}{4}$
C、1
D、2
展开答案
答案:【C】
解:从起点A到最高点B可看做平抛运动的逆过程,如图所示:
运动员做平抛运动,初速度方向与水平方向夹角的正切值为:
$tan a = 2 tan \beta =2\dfrac{h}{\dfrac{x}{2}}=\dfrac{4h}{x}=\dfrac{4×2.06}{8.16}=1$
故ABD错误,C正确;
如图所示为一物体做平抛运动轨迹的一部分,测得轨迹上A、B间和B、C间水平距离均为a,竖直距离分别为b和2b。已知物体质量为m,重力加速度为g。则该物体平抛的初动能为( )
A:$\dfrac{2mga^2}{b}$
B:$\dfrac{2mga^2}{g}$
C:$\dfrac{mga^2}{2g}$
D:$\dfrac{mga^2}{2b}$
展开答案
【答案】D
【解析】看到图线题目,一定要考虑横坐标和纵坐标的物理意义,如果一眼看不出来,那就转换一下!!!!
横向是匀速,所以横向长度就可转换成时间!!!
纵向对应的时间也会相同!
$2b-b=aT^2$
$T=\sqrt{\dfrac{b}{g}}$
$a=\dfrac{a}{T}=a\sqrt{\dfrac{g}{b}}$
$E_k=\dfrac{1}{2}mv^2=\dfrac{mga^2}{2b}$
所以选D
一滑雪运动员以一定的初速度从一平台上滑出,刚好落在一斜坡上的B点,且与斜坡没有撞击,则A、B两点连线与竖直方向所成夹角a和斜坡倾角0的关系为( )
A:$tan\theta \cdot \dfrac{1}{tana}=2$
B:$tan\theta \cdot tana=2$
C:$tana \cdot \dfrac{1}{\theta}=2$
D:$tan\theta \cdot tana=1$
展开答案
【答案】B
曲线运动还是多考虑角度的物理意义,然后让他变成数学!
