圆周运动经典例题
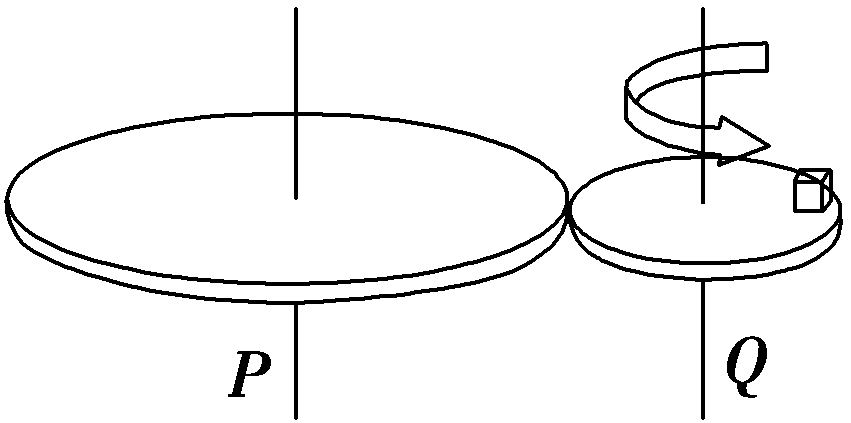
(2020·资阳诊断)如图所示，水平放置的两个用相同材料制成的轮P和Q靠摩擦传动，两轮的半径R∶r ＝2∶1.当主动轮Q匀速转动时，在Q轮边缘上放置的小木块恰能相对静止在Q轮边缘上，此时Q轮转动的角速度为ω1，木块的向心加速度为a1，若改变转速，把小木块放在P轮边缘也恰能静止，此时Q轮转动的角速度为ω2，木块的向心加速度为a2，则
A.$\dfrac{\omega_1}{\omega_2}=\dfrac{1}{2}$ B.$\dfrac{\omega_1}{\omega_2}=\dfrac{\sqrt{2}}{1}$
C.$\dfrac{a_1}{a_2}=\dfrac{1}{1}$ D.$\dfrac{a_1}{a_2}=\dfrac{1}{2}$
展开答案
【答案】：C
【解析】：根据题述，$a_1=\omega_1^2r$，$ma_1=\mu mg$，联立解得$\mu g=\omega_1^2r$。小木块放在P轮边缘也恰能静止，$\mu g=\omega^2R=2\omega^2r$.由$\omega R=\omega_2r$，联立解得$\dfrac{\omega_1}{\omega_2}=\dfrac{\sqrt{2}}{2}$，选项A、B错误；ma2＝μmg，所以.$\dfrac{a_1}{a_2}=\dfrac{1}{1}$，选项C正确，D错误．
关键点在于力是相等的！！！！物理的解题基本思路就是找等式。(多选)(2021·江苏省如东县第一次检测)在修筑铁路时，弯道处的外轨会略高于内轨。如图所示，当火车以规定的行驶速度转弯时，内、外轨均不会受到轮缘的挤压，设此时的速度大小为v，重力加速度为g，两轨所在面的倾角为θ，则( )
A．该弯道的半径$r=\dfrac{v^2}{gtan\theta}$
B．当火车质量改变时，规定的行驶速度大小不变
C．当火车速率大于v时，内轨将受到轮缘的挤压
D．当火车速率小于v时，外轨将受到轮缘的挤压
展开答案
【答案】AB
【解析】火车拐弯时不侧向挤压车轮轮缘，靠重力和支持力的合力提供向心力，设转弯处斜面的倾角为θ，根据牛顿第二定律得$mgtan\theta=m\dfrac{v^2}{r}$，解得$r=\dfrac{v^2}{gtan\theta}$，故选项A正确；
根据牛顿第二定律得$mg tan\theta=m\dfrac{v^2}{r}$ ，解得$v=\sqrt{grtan \theta}$，可知火车规定的行驶速度与质量无关，故选项B正确；
当火车速率大于v时，重力和支持力的合力不够提供向心力，此时外轨对火车有侧压力，轮缘挤压外轨，故选项C错误；
当火车速率小于v时，重力和支持力的合力大于所需的向心力，此时内轨对火车有侧压力，轮缘挤压内轨，故选项D错误。
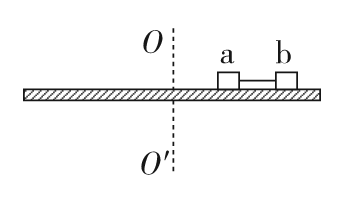
两个质量分别为2m和m的小木块a和b（可视为质点）放在水平圆盘上，a与转轴OO′的距离为L，b与转轴的距离为2L，a、b之间用长为L的强度足够大的轻绳相连，木块与圆盘间的最大静摩擦力为木块所受重力的k倍，重力加速度大小为g。若圆盘从静止开始绕转轴缓慢地加速转动，开始时轻绳刚好伸直但无张力，用ω表示圆盘转动的角速度，下列说法正确的是（ ）
A．a比b先达到最大静摩擦力
B．a、b所受的摩擦力始终相等
C．$\omega=\sqrt{\dfrac{kg}{2L}}$是b开始滑动的临界角速度
D．当$\omega=\sqrt{\dfrac{2kg}{3L}}$时，a所受摩擦力的大小为$\dfrac{5kmg}{3}$
展开答案
【答案】D
【解析】A．木块随圆盘一起转动，当绳子上无拉力时，静摩擦力提供向心力，由牛顿第二定律得
$F_f=mω^2r$，$F_{fmax}=kmg$
联立得
$ω_{max}=\sqrt{\dfrac{kg}{r}}$
故随着ω增大，b先达到临界角速度，b先达到最大静摩擦力，A错误；
B．在b的静摩擦力没有达到最大前，由
$F_f=mω^2r$
a、b质量分别是2m和m，而圆周运动的半径r分别为L和2L，所以开始时a和b受到的摩擦力是相等的；当b受到的静摩擦力达到最大后，即
$ω>\sqrt{\dfrac{kg}{2L}}$
对于b木块有
$kmg＋F=mω^2·2L$
对于a木块有
$F_f -F=2mω^2L$
联立得
$F_f=4mω^2L-kmg>kmg$
可知二者受到的摩擦力不一定相等，B错误；
C．b刚要滑动时，对b木块有
$kmg+F=mω_0^2·2L$
对a木块有
$k·2mg-F=2mω_0^2·L$
联立解得
$\omega_0=\sqrt{\dfrac{3kg}{4L}}$
C错误。
D．当
$\omega=\sqrt{\dfrac{2kg}{3L}}$
时，b未滑动，a所受摩擦力大小
$F_f=4mω^2L-kmg=\dfrac{5kmg}{3}$
D正确。
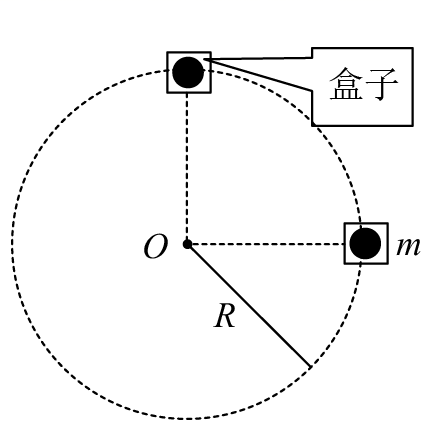
如图所示，质量为m的小球置于立方体的光滑盒子中，盒子的边长略大于球的直径。某同学拿着该盒子在竖直平面内做半径为R的匀速圆周运动，已知重力加速度为g，空气阻力不计，要使在最高点时盒子与小球之间作用力恰为mg，则（ ）
A．该盒子做匀速圆周运动的周期一定小于$\pi\sqrt{\dfrac{2R}{g}}$
B．该盒子做匀速圆周运动的周期一定等于$\pi\sqrt{\dfrac{2R}{g}}$
C．盒子在最低点时盒子与小球之间的作用力大小可能小于3mg
D．盒子在最低点时盒子与小球之间的作用力大小可能大于3mg
展开答案
【答案】B
【解析】AB．要使在最高点时盒子与小球之间恰好为mg，则盒子顶部对小球必然有向下的弹力mg，根据牛顿第二定律则有
$mg+mg=m\dfrac{v^2}{R}$
解得出该盒子做匀速圆周运动的速度
$v=\sqrt{2gR}$
该盒子做匀速圆周运动的周期为
$T=\dfrac{2\pi R}{v}=\pi\sqrt{\dfrac{2R}{g}}$
故A错误，B正确；
CD．在最低点时，盒子与小球之间的作用力和小球重力的合力提供小球运动的向心力，由牛顿第二定律则有
$F-mg=m\dfrac{v^2}{R}$
解得
$F=3mg$
故CD错误。
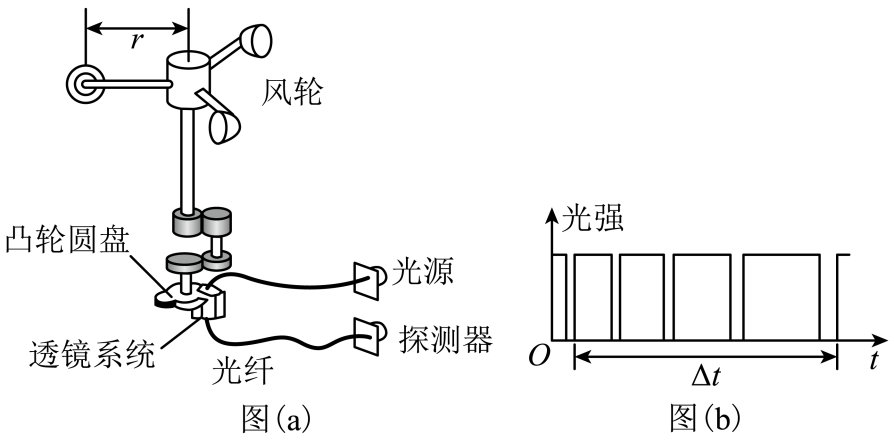
风能是可再生清洁能源，我国在风力发电方面的研究处于世界前列。在风能开发利用时，常用到风速仪，其结构如图（a）所示。光源发出的光经光纤传输，被探测器接收，当风轮旋转时，通过齿轮带动凸轮圆盘旋转，当圆盘上的凸轮经过透镜系统时光被遮挡。已知风轮叶片转动半径为r，每转动n圈带动凸轮圆盘转动一圈，凸轮每次经过透镜系统时，光线被挡住，接收不到光。若某段时间$\Delta t$内探测器接收到的光强随时间变化关系如图（b）所示，则该时间段内风轮叶片（ ）
A．转速逐渐增大，平均速率为$\dfrac{8\pi nr}{\Delta t}$ B．转速逐渐增大，平均速率为$\dfrac{4\pi nr}{\Delta t}$
C．转速逐渐减小，平均速率为$\dfrac{8\pi nr}{\Delta t}$ D．转速逐渐减小，平均速率为$\dfrac{4\pi nr}{\Delta t}$
展开答案
【答案】C
【解析】根据题意,从题图乙可以看出，在$\Delta t$时间内，探测器接收到光的时间越来越长，凸轮圆盘的挡光时间也越来越长，可以确定凸轮圆盘的转速在减小,即风轮叶片转动得越来越慢，从题图乙可以看出在$\Delta t$时间内有4次挡光，即凸轮圆盘转动了4周，风轮叶片转动了4n周，风轮叶片转过的弧长
$I=4n \times 2\pi r$
风轮叶片转动的平均速率
$\bar v = \dfrac{8 \pi n r}{\Delta t}$
故C正确。
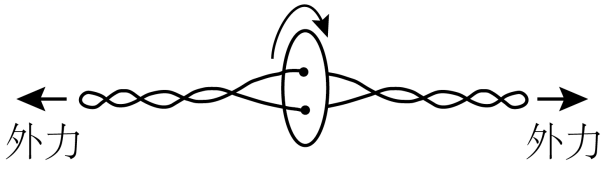
（2021·全国高考真题）“旋转纽扣”是一种传统游戏。如图，先将纽扣绕几圈，使穿过纽扣的两股细绳拧在一起，然后用力反复拉绳的两端，纽扣正转和反转会交替出现。拉动多次后，纽扣绕其中心的转速可达50r/s，此时纽扣上距离中心1cm处的点向心加速度大小约为（ ）
A．10m/s2 B．100m/s2 C．1000m/s2 D．10000m
展开答案
【答案】C
【解析】纽扣在转动过程中
$\omega =2\pi n=100\pi rad/s$
由向心加速度
$a =\omega ^2r=1000m/s^2$
(2020·全国卷Ⅰ，16)如图，一同学表演荡秋千。已知秋千的两根绳长均为10 m，该同学和秋千踏板的总质量约为50 kg。绳的质量忽略不计。当该同学荡到秋千支架的正下方时，速度大小为8 m/s，此时每根绳子平均承受的拉力约为( )
A.200 N B.400 N C.600 N D.800 N
展开答案
【答案】B
该同学身高相对于秋千的绳长可忽略不计，可以把该同学看成质点。当该同学荡到秋千支架的正下方时，由牛顿第二定律有$2F-mg=\dfrac{mv^2-}{L}$，代入数据解得F＝410 N，选项B正确。
(多选)(2021·天津市六校期末联考)如图所示，轻杆一端套在光滑水平转轴O上，另一端固定一质量为m＝1 kg的小球，使小球在竖直平面内做半径为R＝0.4 m 的圆周运动。设运动轨迹的最低点为A点，最高点为B点，不计一切阻力，重力加速度为g＝10 m/s2，下列说法中正确的是( )
A.要使小球能够做完整的圆周运动，则小球通过B点的速度至少为2 m/s
B.若小球通过B点的速度为1 m/s时，杆对小球的作用力为7.5 N，方向向上
C.小球能过最高点B时，杆对小球的作用力大小一定随着小球速度的增大而增大
D.小球能过最高点B时，杆对小球的作用力大小可能为零
展开答案
【答案】 BD
【解析】 在最高点，由于杆能支撑小球，所以小球在最高点B时的速度可以恰好为零，故A错误；设竖直向下为正方向，在B点由牛顿第二定律有$mg+F=m\dfrac{v^2}{R}$，得$F=m\dfrac{v^2}{R}-mg=(1\times \dfrac{1^2}{0.4}-1\times 10)N=-7.5N$，负号说明杆对小球的作用力方向竖直向上，故B正确；
在最高点，若小球所受的杆的作用力方向向上，根据牛顿第二定律$mg-F=m\dfrac{V^2}{R}$，若增大小球的速度，则F减小，若小球受杆的弹力方向向下，则$mg＋F＝m\dfrac{v^2}{R}$，v增大，F增大，当$V=\sqrt{gR}=2m/s$时，F＝0，故C错误，D正确。
(2021·陕西西安中学第二次模拟)长均为L的两根轻绳，一端共同系住质量为m的小球，另一端分别固定在等高的A、B两点，A、B两点间的距离也为L，重力加速度大小为g。今使小球在竖直平面内以A、B连线为轴做圆周运动，若小球在最高点速率为v时，两根绳的拉力恰好均为零，则小球在最高点速率为2v时，每根绳的拉力大小均为( )
A.$\sqrt{3}mg$ B.$2\sqrt{3}mg$
C.$3mg$ D.$\dfrac{4\sqrt{3}mg}{3}$
展开答案
【答案】A
【解析】小球在最高点速率为v时，两根绳的拉力恰好均为零，有$mg=m\dfrac{v^2}{r}$；当小球在最高点的速率为2v时，根据牛顿第二定律有$mg+2F_T cos30°= m\dfrac{(2v)^2}{r}$，解得$F_T=\sqrt{3}mg$，故选项A正确。
(2021·上海市闵行区一模)如图所示，半径为R光滑圆轨道固定在竖直平面内，水平轨道AB在圆轨道最低点与其平滑连接，AB长度为L.小球在外力作用下，由A向B以加速度a做匀加速运动，到达B点撤去外力．要使小球能沿圆轨道运动到D点，则小球过C点的最小速度值和在A点的最小速度值分别为( )
A．$v_C＝0$，$vA＝2Rg$
B．$v_C＝\sqrt{gR}$，$v_A＝\sqrt{5gR-2aL}$
C．$v_C＝\sqrt{gR}$，$v_A＝\sqrt{5gR}$
D．$v_C＝\sqrt{gR}$，$v_A＝\sqrt{5gR+2aL}$
展开答案
【答案】B
【解析】：小球恰能经过C点时速度最小，则根据$mg=m\dfrac{v_c^2}{R}$，解得$v_C＝\sqrt{gR}$；根据动能定理，
从B到C：$\dfrac{1}{2}mv_B^2=\dfrac{1}{2}mv_c^2+2mgR$，解得$v_B=\sqrt{5gR}$；
从A到B：$V_B^2-v_B^2=2aL$ ，解得$v_A＝\sqrt{5gR+2aL}$
一转动装置如图所示，两根轻杆0A和AB与一小球以及一小环通过铰链连接，两轻杆长度相同，球和环的质量均为m，0端通过铰链固定在竖直的轻质转轴上，套在转轴上的轻质弹簧连接在0与小环之间，原长为L，装置静止时，弹簧长为之$\dfrac{3L}{2}$。转动该装置并缓慢增大转速，小环缓慢上升。弹簧始终在弹性限度内，忽略一切摩擦和空气阻力，重力加速度为g,求:
（1)弹簧的劲度系数k;
（2）AB杆中弹力为零时，装置转动的角速$\omega$
展开答案
【答案】B
【解析】：1)可以单独分析，也可以整体分析，整体的话，A所有的重力肯定会被OB两点均分，一人分一半。
所以$\dfrac{mg}{2}+mg=k\dfrac{L}{2}$
解得：$k=\dfrac{3mg}{L}$
2)当AB完全不受力，那么弹簧只受mg的重力，伸长量为
$\Delta x = \dfrac{mg}{k}$
$\Delta x =\dfrac{L}{3}$
此时OB的长度为$\dfrac{4L}{3}$
$\omega ^2Rm=T$
$\dfrac{T}{R}=\dfrac{mg}{\dfrac{2L}{3}}$
解得：$\sqrt{\dfrac{3g}{2L}}$
