曲线运动
一、曲线运动的知识点
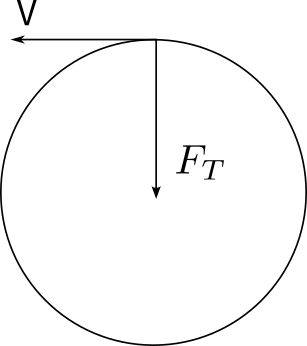
定义:轨迹是一条曲线的运动叫曲线运动。
条件:质点所受合外力的方向跟他的速度方向不在一条直线。
特点:
1、速度方向是曲线的切线方向
2、轨迹是一条曲线
3、速度的方向时刻在改变,所以变速运动必然具有加速度。
二、运动的合成与分解
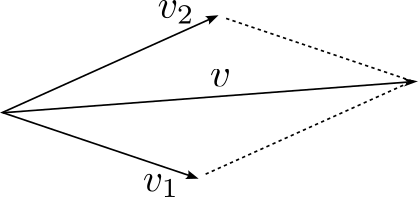
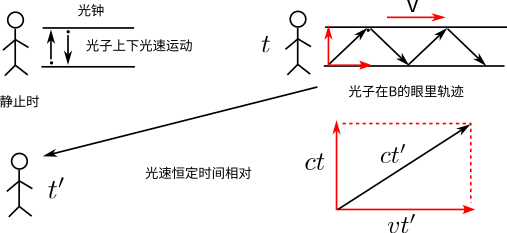
等时性:各分运动的时间与合运动的时间相同。毕竟在同一个时空
独立性:各个分运动独立进行,不受其他运动影响,这也是解题的关键思路。
等效性:各个分运动叠加起来与合运动有相同的效果。
小船渡河
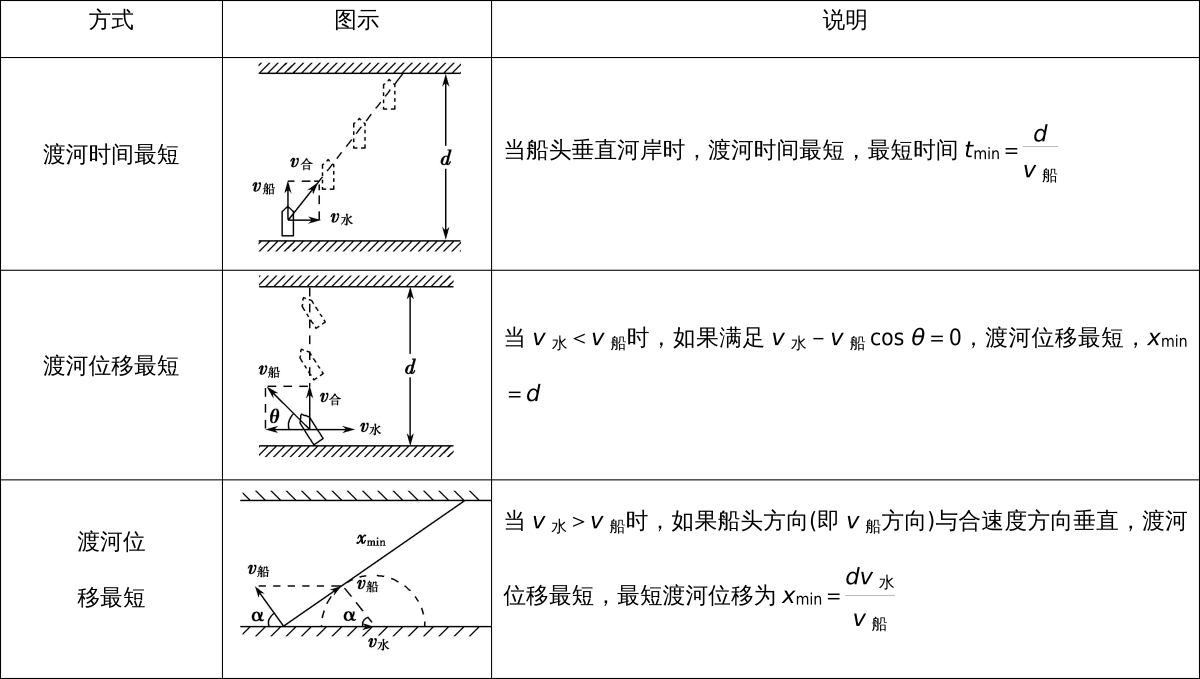
解题思路:
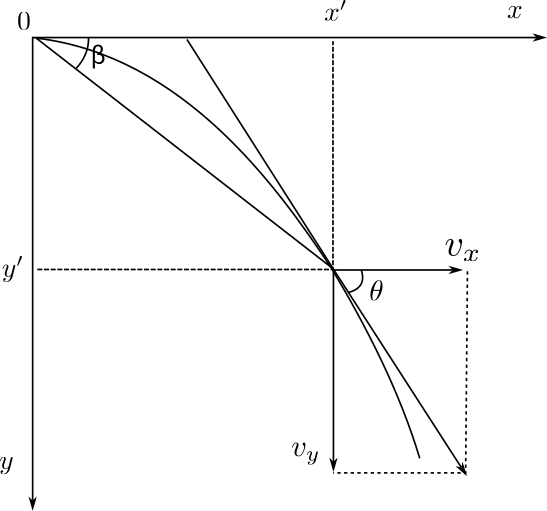
1.基本规律
水平速度:
竖直速度:
合速度大小:
速度关系:
位移关系:
推论:
以上的等式都是解题的关键点。
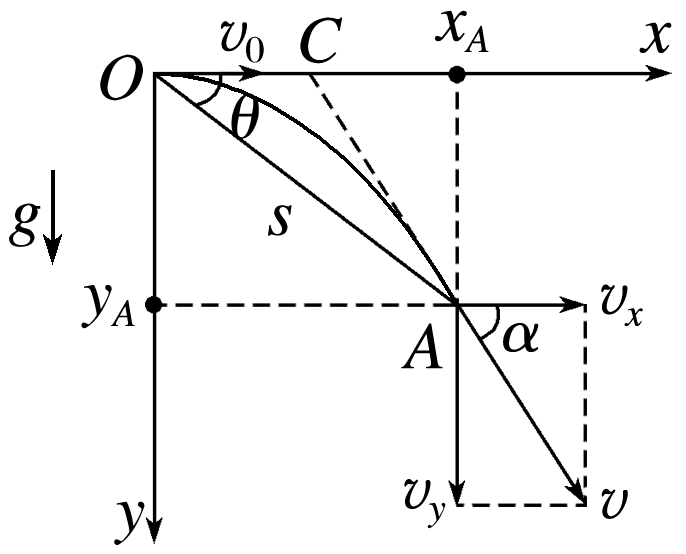
模型
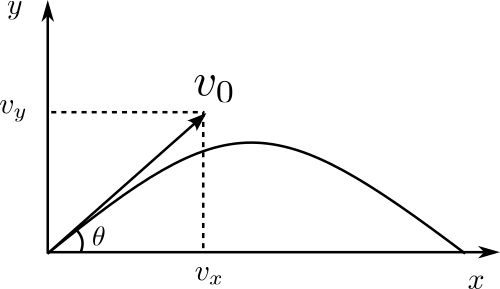
水平方向:
竖直方向:
飞行时间:
无论哪一种题型,关键点都是找等式,然后列方程,如此才能得出正确结果。

描述圆周运动的物理量
加速度和力的关系:F=am
线速度的定义:
角速度的定义:
线速度和周期的关系
角速度周期的关系:
关系:
周期和频率的关系:
知道定义和关系,一切推导就会顺其自的推出来。
F的形式模型:F=am 是解决圆周运动的核心。
轻绳轻杆模型
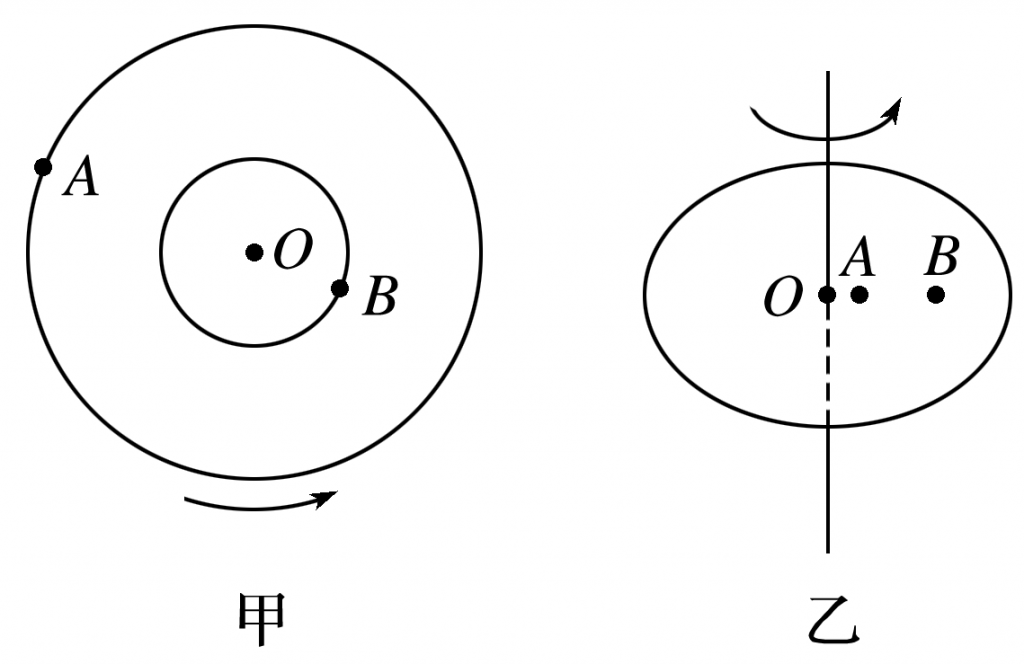
(1)皮带传动:如图甲、乙所示,皮带与两轮之间无相对滑动时,两轮边缘线速度大小相等,即vA=vB.
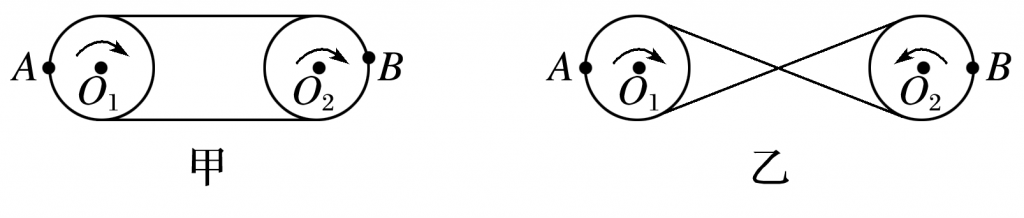
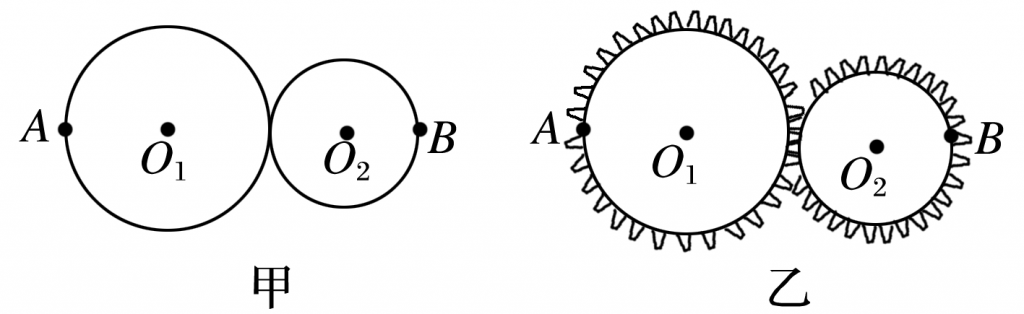
(2)摩擦传动和齿轮传动:如图甲、乙所示,两轮边缘接触,接触点无打滑现象时,两轮边缘线速度大小相等,即vA=vB.
(3)同轴转动:如图甲、乙所示,绕同一转轴转动的物体,角速度相同,ωA=ωB,由v=ωr知v与r成正比.