力的合成与分解
一 讲核心素养
1.物理观念:受力分析、平衡条件。科学思维:整体法、隔离法、合成法、分解法、矢量三角形法、相似三角形法、拉密定理。
这个专题题目类型, 基本和方法对应,题目千千万,方法就一变。
\begin{gather} \begin{split} \varphi(x,z) &= z – \gamma_{10} x – \sum_{m+n\ge2} \gamma_{mn} x^m z^n\\ &= z – M r^{-1} x – \sum_{m+n\ge2} M r^{-(m+n)} x^m z^n \end{split}\tag{4.a}\label{eq:4a}\\ \begin{split} \zeta^0 &= (\xi^0)^2, \\ \zeta^1 &= \xi^0 \xi^1 \end{split}\notag \end{gather}
(1).能用整体法、隔离法、等分析多物体系的受力情况。
(2)会利用合成法、分解法求解静态平衡类问题。
(3)会用矢量三角形法、相似三角形法、拉密定理等分析动态平衡问题。
2.科学态度与责任:在生产、生活情境中,体验物理学技术的应用。
能用静力学的知识解决以生活中的实际问题为背景的问题,体会物理学的应用价值激发学生学习欲望。
二 讲必备知识
【知识点一】 物体的受力分析
1.高中力学中的五种力
| 种类 | 大小 | 方向 |
| 重力 | $G=mg$(不同高度、纬度、g不同) | 竖直向下 |
| 弹簧弹力 | $F=kx$(x为形变量) | 沿弹簧轴线 |
| 静摩擦力 | 0<Ff静≤Ffmax | 与相对运动趋势方向相反 |
| 滑动摩擦力 | Ff滑=μFN | 与相对运动方向相反 |
| 万有引力 | $F=G \frac{m_1 m_2}{R^2}$ | 沿质点间的连线 |
2.力的合成与分解
(1)合成 分解很难分开讲,他们只遵循一个原则“平行四边形原则”
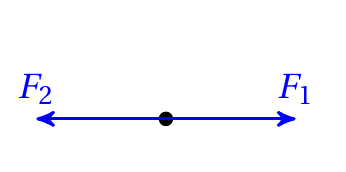
对于平面内任意两个力的合成与分解只需遵从平行四边形原则,这是一个非常容易理解和实践的。
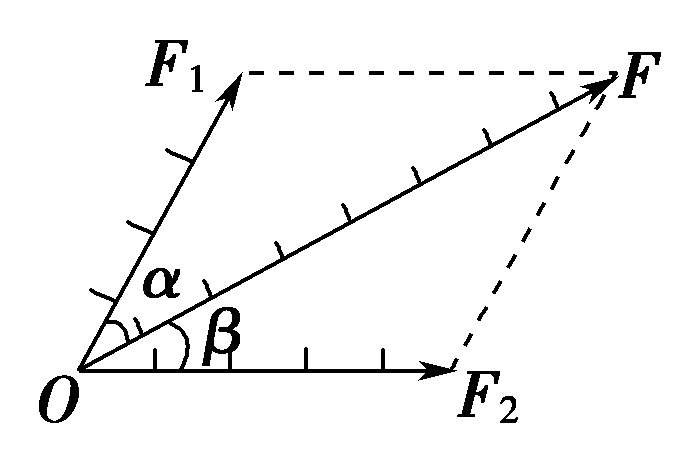
作图方法:从力的作用点起,按同一标度作出两个分力F1和F2的图示,再以F1和F2的图示为邻边作平行四边形,画出过作用点的对角线,量出对角线的长度,计算出合力的大小,量出对角线与某一力的夹角确定合力的方向(如图所示)。
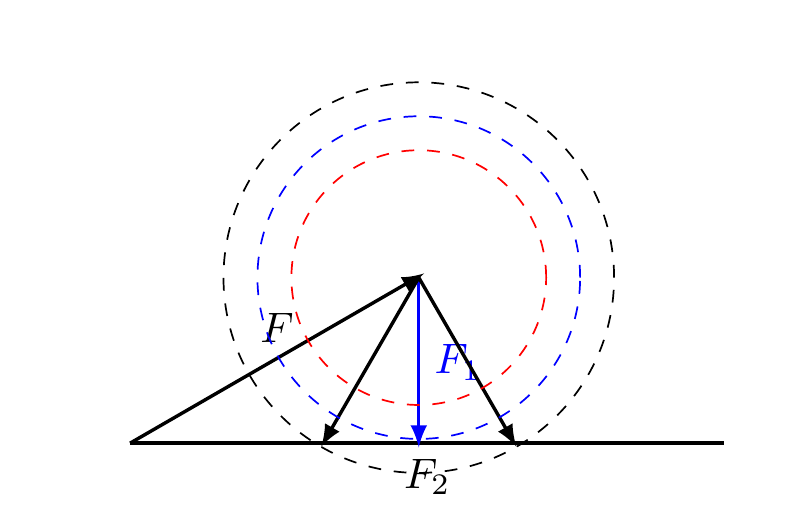
当一个力的大小确定,另一个只有方向确定,那么解就不是唯一的了,如图,F大小方向确定,F2方向水平,那么F1的解会有三种情况,对应三种颜色的圈,红色圈不能围成三角形,所以没有解,蓝色圈只有一个焦点,所以一个解,黑色圈有两个焦点,所以有两个解。
(2)计算法:几种特殊情况的共点力的合成。
| 类型 | 作图 | 合力的计算 |
| ①互相垂直 | 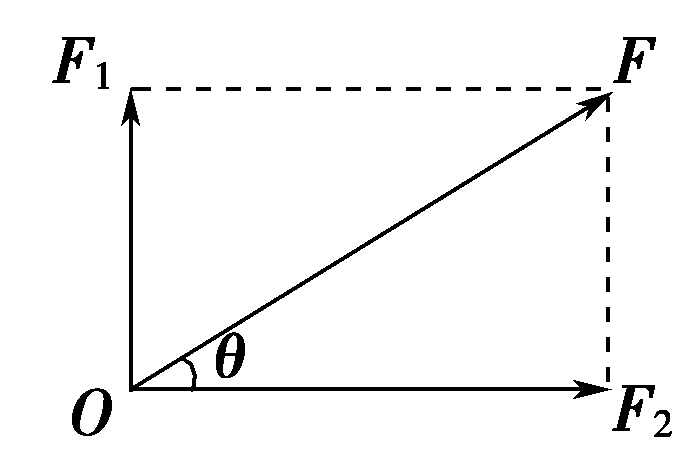 | F=$\frac{F_1}{sin\theta}$ |
| ②两力等大,夹角为θ | 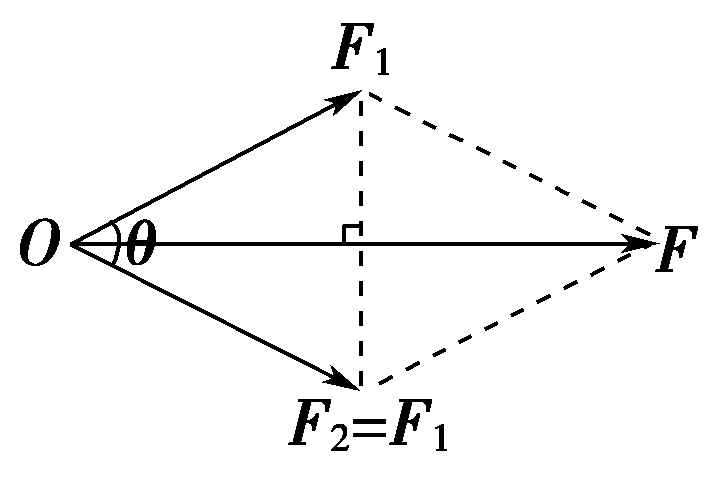 | F=2F1cosθ |
| ③两力等大且夹角为120° | 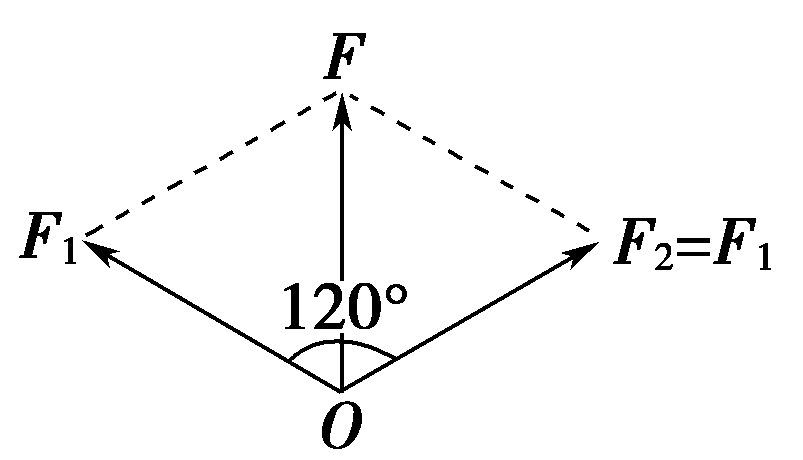 | 合力与分力等大 |
1586年,荷兰的斯蒂文在《静力学基础》一书中最早提出力的分解与合成原理,并把这一原理(没有明确表达出)应用到两绳悬一重物、一绳在三处挂不同重物等场景中,解决了许多复杂问题。
1687年,牛顿在《自然哲学的数学原理》的“物体的运动”的推论1、2中分别写到:“一个物体,同时受到两个力的作用,就将沿平行四边形的对角线运动,所用的时间和它分开受到这两个力的作用而沿两边运动的时间相同”。牛顿凭借敏锐的直觉,推断出了运动和力的分解与合成所遵循的定则,但未作进一步的证明。
几乎与此同时,法国皮耶利·瓦里翁向巴黎科学院提交了由他独立得出的诸力合成的平行四边形定则的报告,但没有表述清楚。1725年,瓦里翁在《新力学或静力学》一书中用力的合成与分解原理解决了各种具体静力学问题,并初步提出了“力矩”概念,找出了力的平行四边形原理与力矩的关系。他还把力的平行四边形原理推广到运动学的速度中去,认为静力学只是动力学的特例。
1726年,约翰·伯努利在写给瓦里翁的信中提出力的平行四边形原理可以用于静力学。他用虚功原理分析在一个力学系统中力矩做功的问题,指出在任何力的平衡的情况下,无论这些力是直接地或是间接的用来支持相互平衡。丹尼尔·伯努利则在《力学原理的研究及力的分解与合成证明》一文中对瓦里翁提出两点质疑:①力与速度在运用合成与分解时不应成正比;②在各力的作用下物体的运动是不是具有独立性。
此后,法国的潘索也对平行四边形定则进行了数学证明并首先引入“刚体”、“力偶”等概念,进一步将静力学用于刚体及机器结构的分析上。直到十九世纪乃至二十世纪初,包括拉普拉斯、茹可夫斯基等众多力学家在内,都花了许多时间来对此进行争论。
如同惯性定律一样,这是一条永远无法用实验完美证明的定则。只是随着矢量及其所遵循的运算定则的确立,力、位移、速度等被纳入力的矢量体系,以及运动的独立性、力的独立作用原理和物体在摩擦力下运动的动力机制被揭示,人们才从逻辑上接受了这一定则。
我们重点说下Stevin:为什么两力可以用平行四边形相加?这是需要证明的,让我们从静力平衡开始推理,想像一物被绑了三条绳索,各绳拉开而物不动,问各绳出力多少?
出力推算,早在牛頓前100年,见于Simon Stevin (1548年-1620年) 的天才构想,想像一重物在斜坡上被一绳拉住,这重物另外受本身重力,以及斜坡的支持力。
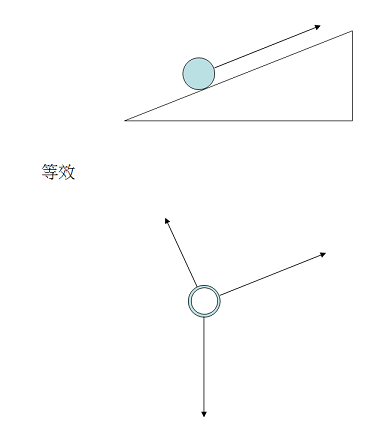
球若没有绳的拉力将会下滑,故绳的拉力向上。于是三力汇聚在球心一点。
接着 Simon Stevin 用项链平衡法算出绳的拉力。项链平衡法是天才构想,它示范了如何把不对称现象转换成对称现象。
Stevin 称右上绳力为斜坡力,他证明了斜坡支持力 x 斜坡球数=直坡力 x 直坡球数。
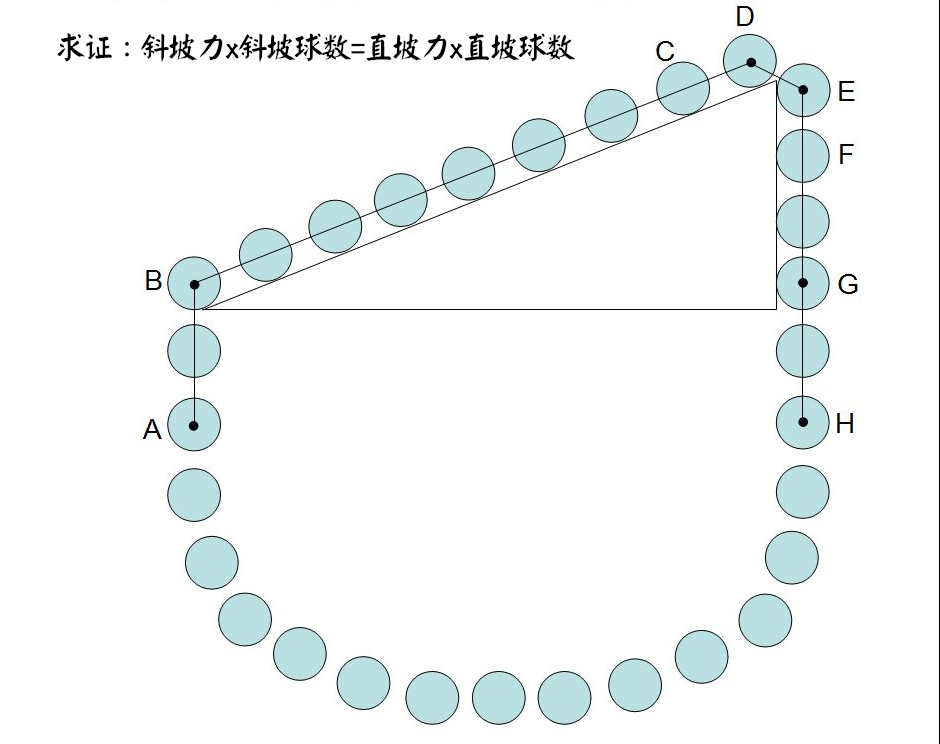
有个三角斜坡挂一球链,链最终静止,斜坡底球B受弧状链向下拉力F.
问:直坡底球G受弧状链向下拉力多少?
答:底下弧状链不管上方斜坡形状如何,只管弧两端,两端必需平等拉住。於是球G和球B平等,球G受向下拉力必也是F.
接著看斜坡和直坡最高球:
斜坡最高球受力= F +斜坡各球拉力。
直坡最高球受力= F +直坡各球拉力。
专心看CDEF与三角形的顶角这角隅,在这角隅画一条角平分线,则CD, EF 对称於左右,而角隅诸物皆静,所以两端拉力必相等。(这里用对称论述了力量可以转向,但力度不变)所以,斜坡最高球受力 = 直坡最高球受力。
即, F+斜坡各球拉力 = F+直坡各球拉力。即,斜坡各球拉力 = 直坡各球拉力。
即,斜坡1球拉力 X 斜坡球数= 直坡1球拉力 X 直坡球数。
证明完毕。

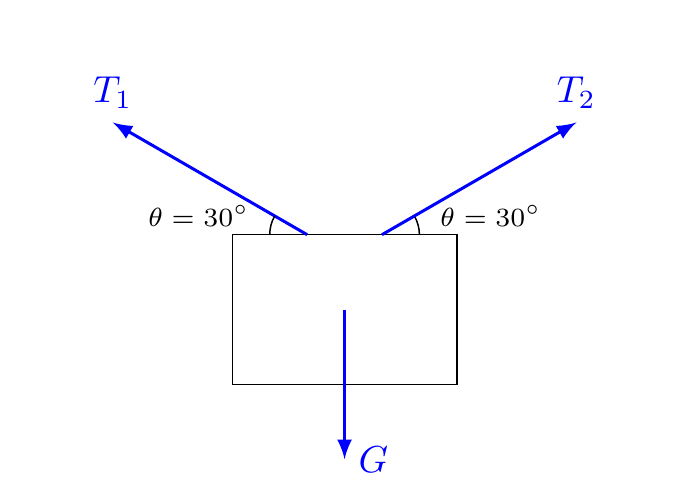
日常中我们合作提物体,学了力的合成与分解,将有助于节省体力,还可以算出各个力的大小。
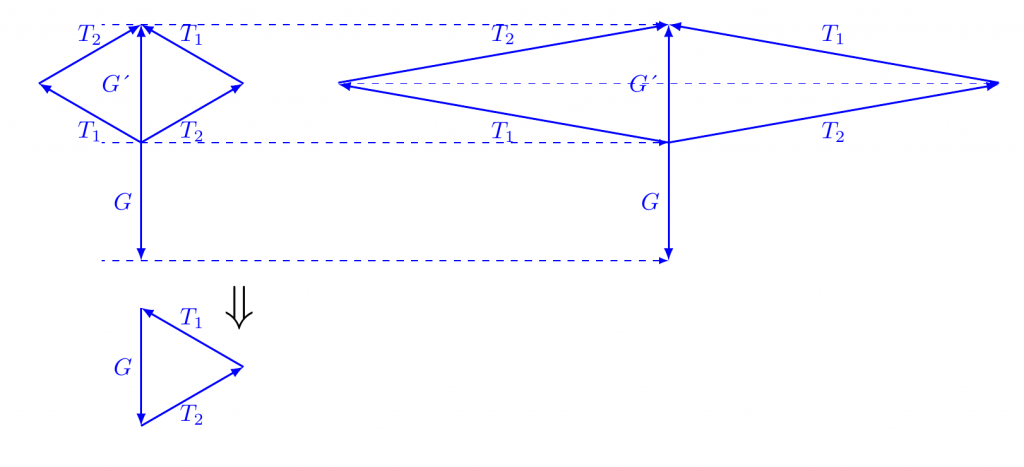
作图一定要标准,平行四边形一定平行,力的大小要和线段的长短 比例,比如上图,重力相等 情况下,$T_1$,$T_2$,夹角越大, 则绳子上的 越大, 这就是为什么输电线不是水平的原因,一旦夹角趋近与180度,$T_1$,$T_2$也将趋近于无穷大,所以输电线要保持适当角度,太低容易碰到树木, 太高容易拉断。
两人合作提物体, 都向上最省力。
3.整体法与隔离法
| 整体法 | 隔离法 | |
| 概念 | 将加速度相同的几个物体作为一个整体来分析的方法 | 将研究对象与周围物体分隔开来分析的方法 |
| 选用原则 | 研究系统外的物体对系统整体的作用力或系统整体的加速度 | 研究系统内物体之间的相互作用力 |
例题
【知识点二】静态平衡问题
1.平衡状态:物体处于静止或匀速直线运动的状态,即a=0.
2.平衡条件:F合=0或Fy=0.
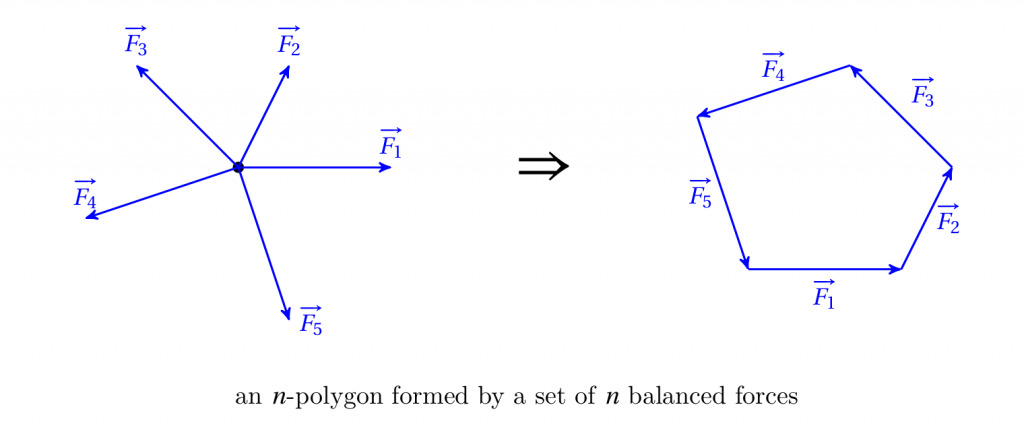
对于共点力,无论多少个力只要能收尾相连,那么最小合力就可以为0,对于三个力的共点力,只要能围成三角形,最小合力就是0,最大合力就是三个力的和。
在组成三角形的三条边中,任意一边大于其他两边之差,任意一边小于其他两边之和,,所以即便是三个力,一旦两个力的和不能大于第三边,合力最小值不是0.
例题:已知三个力分别为2N,3N,7N,那么合力最小值 和最大值分别是多少!
解答:最小值7-2-3=2N,因为2、3、7不能组成三角形,所以最小值不可能是0N,最大值2+3+7=12N3.平衡条件的推论
如果物体在多个共点力的作用下处于平衡状态,其中任何一个力与其余几个力的合力大小相等,方向相反.
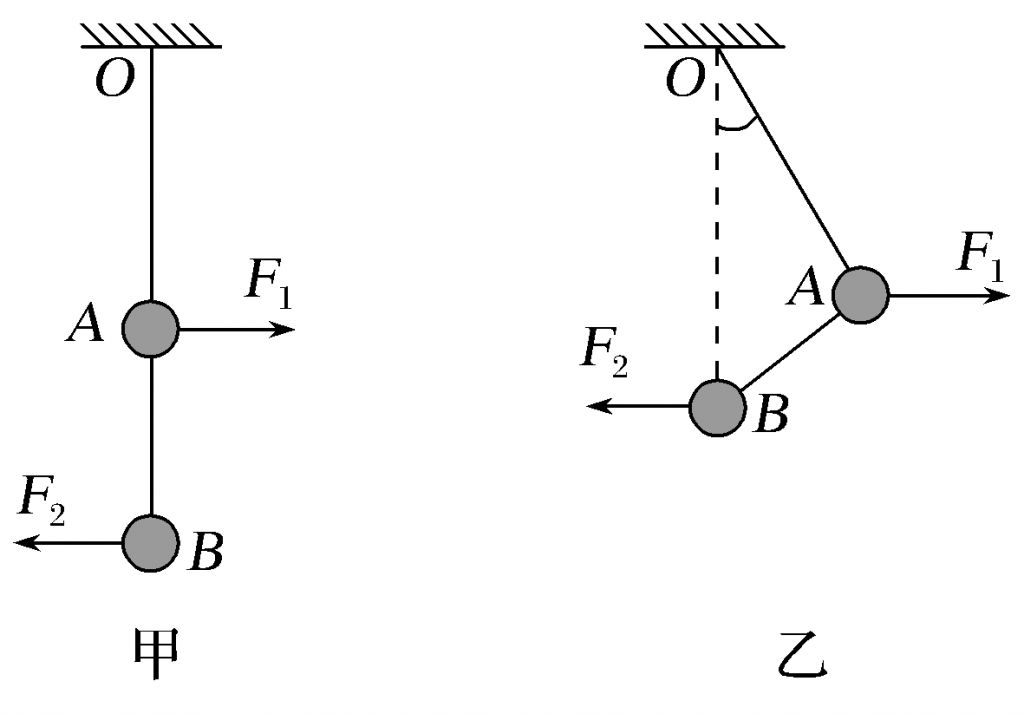
【例】(2020·安徽庐巢七校联盟第三次联考)如图甲所示, A、B两小球通过两根轻绳连接并悬挂于O点,已知两轻绳OA和AB的长度之比为$\sqrt{3}$:1,A、B两小球质量分别为2m和m,现对A、B两小球分别施加水平向右的力F1和水平向左的力F2,两球恰好处于如图乙的位置静止,此时B球恰好在悬点O的正下方,轻绳OA与竖直方向成30°,则( )
A.F1=F2 B.F1=$\sqrt{3}$F2 C.F1=2F2 D.F1=3F2
【解析】 由题意知两轻绳OA和AB的长度之比为$\sqrt{3}$∶1,B球恰好在悬点O的正下方,由几何关系可知,OA与AB垂直;以B球为研究对象,受力示意图如图甲所示,由平衡条件得
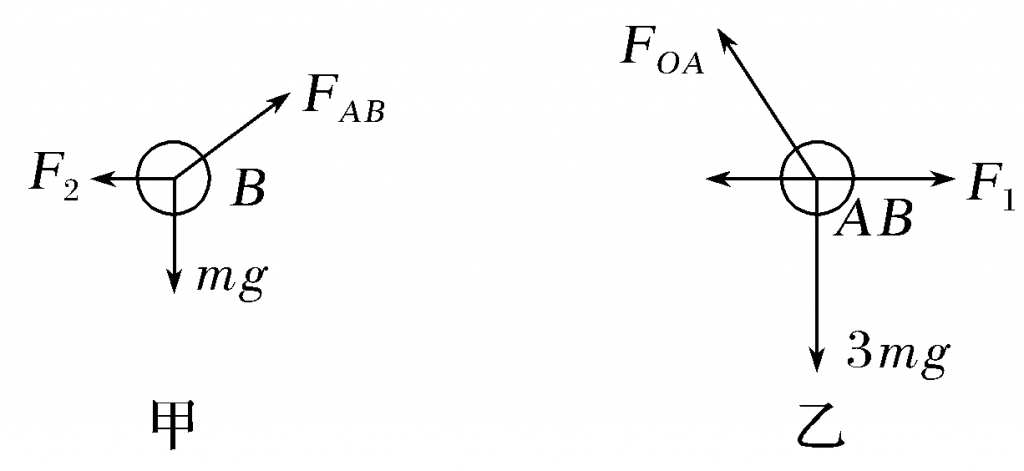
F2=mgtan(90°-30°)=$\sqrt{3}$mg
以A、B两球整体为研究对象,受力示意图如图乙所示,由平衡条件得
F1-F2=3mgtan 30°=$\sqrt{3}$mg
可得F1=2$\sqrt{3}$mg,即F1=2F2,故C正确。
【知识点三】共点力作用下物体的动态平衡
1.动态平衡:“动态平衡”是指物体所受的力一部分是变力,是动态力,力的大小或方向发生变化,但变化过程中的每一个状态均可视为平衡状态,所以叫动态平衡。这是一类难度较高的题目。
2.分析动态平衡问题的方法
| 方法 | 步骤 |
| 解析法 | (1)列平衡方程得出未知量与已知量的关系表达式;(2)根据已知量的变化情况来确定未知量的变化情况 |
| 图解法 | (1)根据已知量的变化情况,画出平行四边形边、角的变化;(2)确定未知量大小、方向的变化 |
| 相似三角形法 | (1)根据已知条件画出两个不同情况对应的力的三角形和空间几何三角形,确定对应边,利用三角形相似知识列出比例式;(2)确定未知量大小的变化情况 |
【例】(多选)如图所示,光滑半球形容器固定在水平面上,O为球心。一质量为m的小滑块,在水平力F的作用下静止于P点。设滑块所受支持力为FN,OP与水平方向的夹角为θ。重力加速度为g,下列关系式正确的是( )
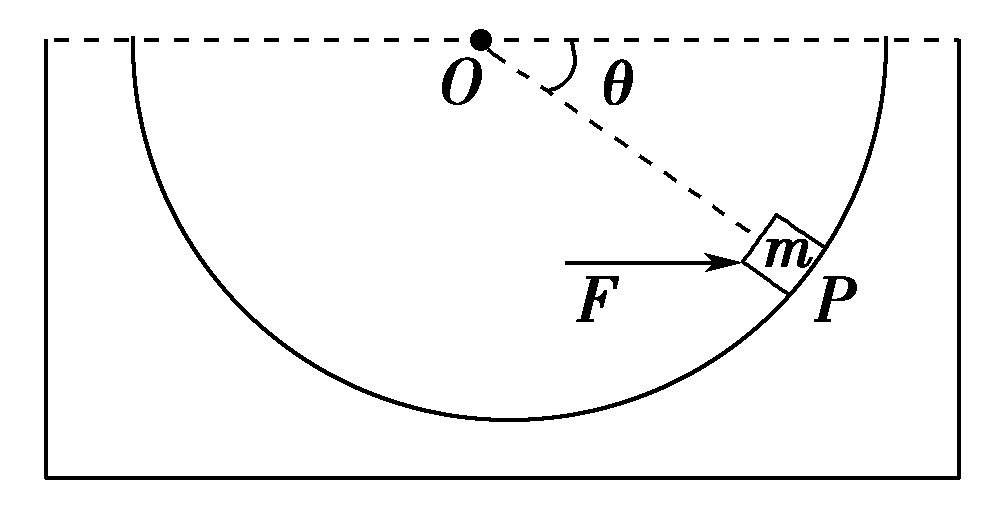
A.$F=\frac{mg}{tan\theta}$ B.$F=mgt an \theta$
C.$F=\frac{mg}{sin\theta}$ D.$F_N=mg tan \theta$
思路点拨:解此题的关键是选取小滑块为研究对象,作好受力分析,根据平衡条件求解。
【答案】AC
【解析】方法一:合成法
滑块受力如图甲,由平衡条件知$ \frac{mg}{F}$=tan θ,
所以$F=\frac{mg}{tan\theta}$,$F=\frac{mg}{sin\theta}$。
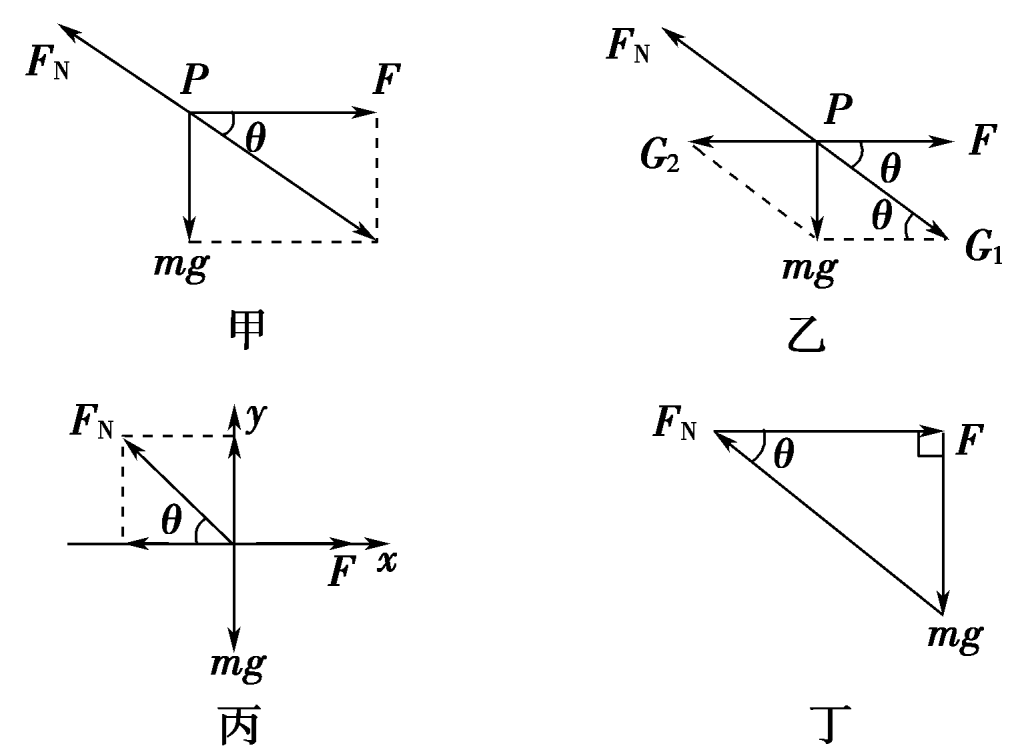
方法二:效果分解法
将重力按产生的效果分解,如图乙所示,
F=G2=$F=\frac{mg}{tan\theta}$,FN=G1=$F=\frac{mg}{sin\theta}$。
方法三:正交分解法
将滑块受的力沿水平、竖直方向分解,如图丙所示,
mg=FNsin θ,F=FNcos θ,
联立解得$F=\frac{mg}{tan\theta}$,$F=\frac{mg}{sin\theta}$
方法四:力的三角形定则法
滑块受到的三个力可组成封闭的三角形,如图丁所示,则由几何关系可得$F=\frac{mg}{tan\theta}$,$F=\frac{mg}{sin\theta}$
三.讲关键能力
【能力点】.会分平衡中的临界与极值问题
1.临界问题:当某物理量变化时,会引起其他几个物理量的变化,从而使物体所处的平衡状态“恰好出现”或“恰好不出现”,在问题的描述中常用“刚好”“刚能”“恰好”等。
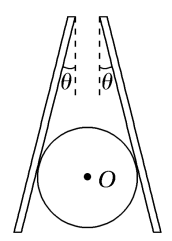
【例题】(2020·河北保定市二模)某位同学用筷子将均匀球夹起悬停在空中,如图9所示,已知球心O与两根筷子在同一竖直面内,小球质量为m,筷子与竖直方向之间的夹角均为θ,筷子与小球表面间的动摩擦因数为μ(最大静摩擦力等于滑动摩擦力),重力加速度为g。每根筷子对小球的压力至少为( )
A.$ \frac{mg}{2(\mu sin\theta – cos\theta)}$ B.$\frac{mg}{2 (\mu cos \theta – sin \theta)}$
C.$ \frac{mg}{ 2(\mu cos \theta + sin\theta)}$ D.$ \frac{mg}{2 (\mu sin\theta -cos\theta)}$
【答案】 B
【解析】 对小球受力分析
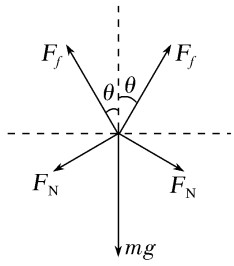
2Ffcos θ=mg+2FNsin θ
Ff=μFN解得FN=$\frac{mg}{2 (\mu cos \theta – sin \theta)}$
2.极值问题:平衡物体的极值,一般指在力的变化过程中的最大值和最小值问题。
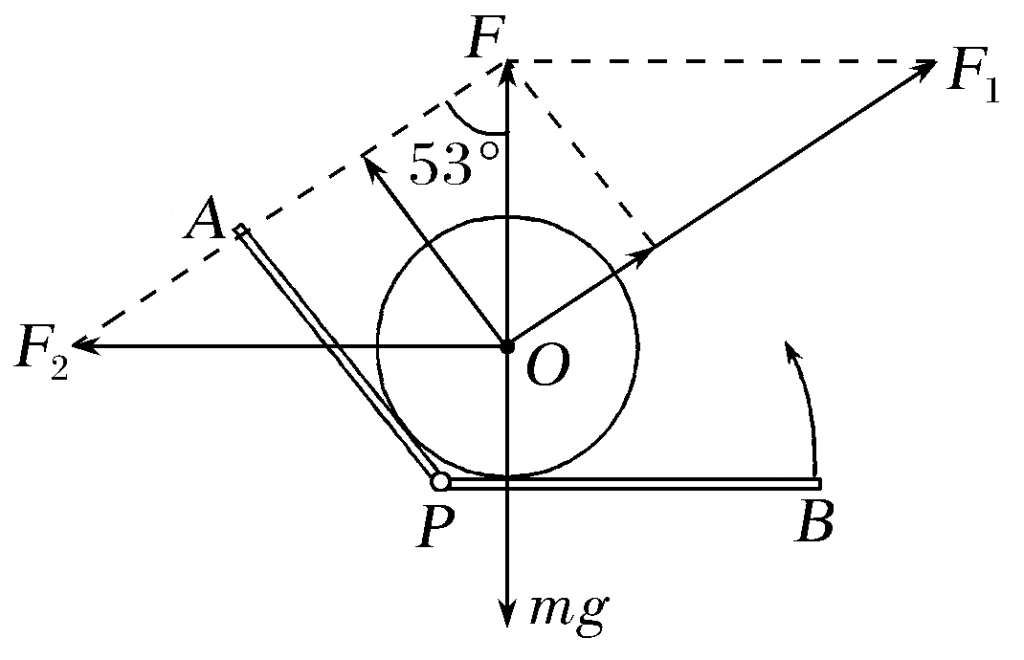
【例】(2021·广东汕头市第一次模拟)如图所示,足够长的光滑平板AP与BP用铰链连接,平板AP与水平面成53°角固定不动,平板BP可绕水平轴在竖直面内自由转动,将一均匀圆柱体O放在两板间。在使BP板由水平位置缓慢转动到竖直位置的过程中,下列说法正确的是( )
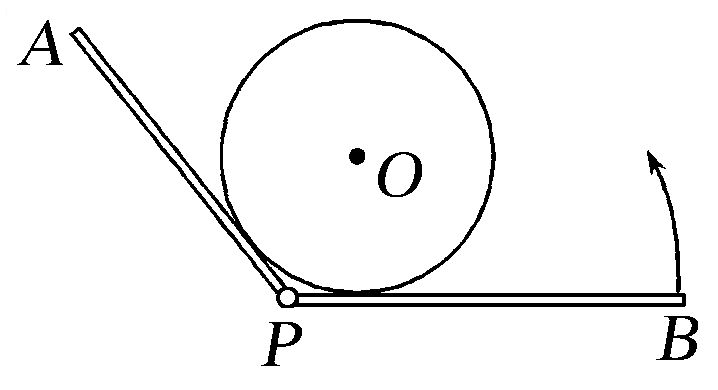
A.当BP沿水平方向时,BP板受到的压力最大
B.当BP沿竖直方向时,AP板受到的压力最大
C.当BP沿竖直方向时,BP板受到的压力最小
D.当BP板与AP板垂直时,AP板受到的压力最小
【答案】 B
【解析】 小球一直处于平衡状态,三个力中的任意两个力的合力与第三个力等值、反向、共线,故F1和F2的合力F一定与重力等值、反向、共线。所以画图时一定要保持重力的长度不变,其他两个力始终在同一个参考系中,这样就可以很方便从图中可以看出力的变化,F1越来越大,F2先变小,后变大,到竖直位置时,F2>mg,故选项B正确,A、C、D错误。
3.解题方法
(1)极限法:首先要正确地进行受力分析和变化过程分析,找出平衡的临界点和极值点;临界条件必须在变化中去寻找,不能停留在一个状态来研究临界问题,而要把某个物理量推向极端,即极大和极小。
(2)数学分析法:通过对问题的分析,依据物体的平衡条件写出物理量之间的函数关系(画出函数图象),用数学方法求极值(如求二次函数极值、公式极值、三角函数极值)。
(3)物理分析方法:根据物体的平衡条件,作出力的矢量图,通过对物理过程的分析,利用平行四边形定则进行动态分析,确定最大值与最小值。
【例2】
四.讲模型思想
“挂件衣钩滑轮”类模型——-正Y模型,死结活结模型。
跨过光滑滑轮(挂钩)的绳上的拉力大小相等
(1)如图甲,绳子左端固定,右端从B点移到C点,两个端点之间水平距离变小,绳子夹角变小,拉力也变小.
(2)如图甲,绳子左端固定,右端从B点移到D点,两个端点之间水平距离不变,绳子夹角不变,拉力也不变.
(3)如图乙,轻杆AB两端连接有轻绳,从水平位置转一个角θ(小于90°),两根绳子之间的夹角变小,所以拉力变小.
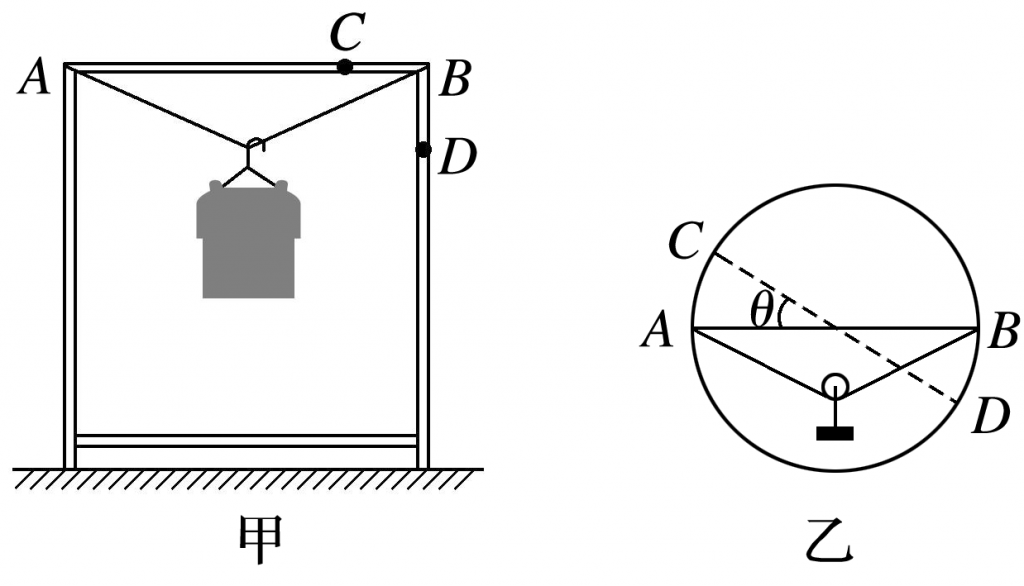
【例】(2020·山东青岛十七中模拟)如图所示,在竖直平面内一根不可伸长的柔软轻绳通过光滑的轻质滑轮悬挂一重物.轻绳一端固定在墙壁上的A点,另一端从墙壁上的B点先沿着墙壁缓慢移到C点,后由C点缓慢移到D点,不计一切摩擦,且墙壁BC段竖直,CD段水平,在此过程中关于轻绳的拉力F的变化情况,下列说法正确的是( )
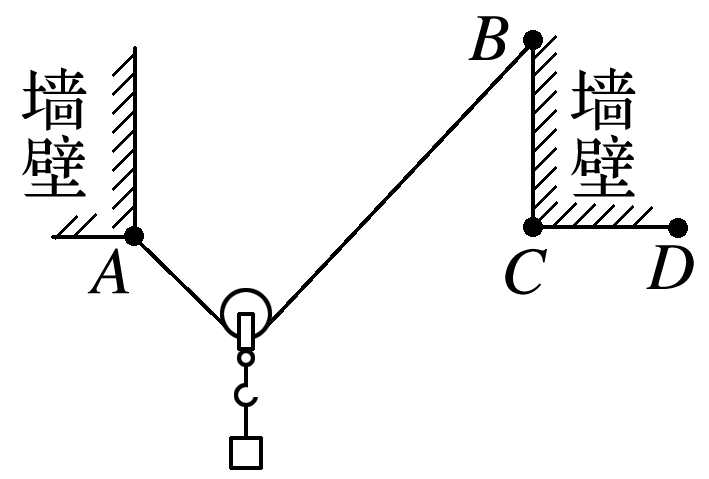
A.F一直减小 B.F一直增大
C.F先增大后减小 D.F先不变后增大
【答案】 D
【解析】 设轻绳总长为L,两竖直墙壁间的距离为s,两段轻绳之间的夹角为2θ,同一根轻绳拉力相等,所以每根轻绳与竖直方向的夹角均为θ,如图所示,根据平衡条件可得:$2Fcos\theta = mg$,所以$F= \frac{mg}{2cos \theta}$
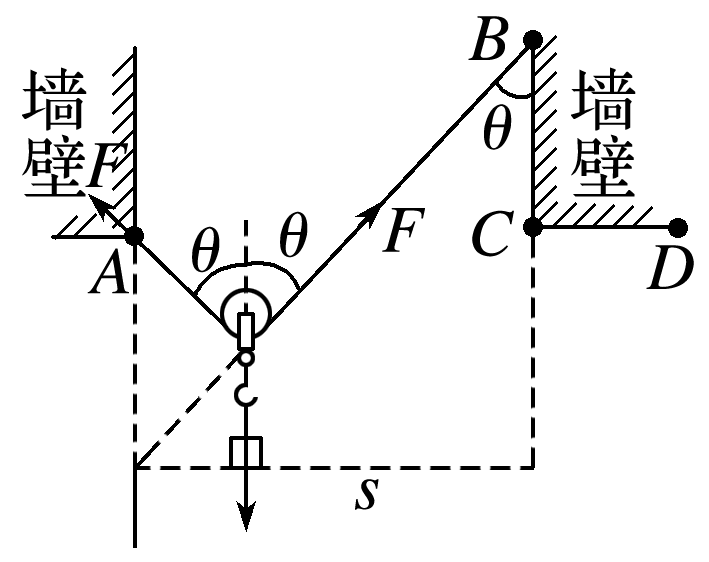
根据图中几何关系结合数学知识得到sin θ=$\frac{s}{L}$;
当轻绳的右端从B点移到C点时,L、s不变,则$\theta$保持不变,则F不变;当轻绳的右端从C点移到D点时,s增大,L不变,θ变大,$cos \theta$变小,则F 增大.所以绳子拉力变化情况为:先不变后增大,故D正确.
