力的合成与分解例题
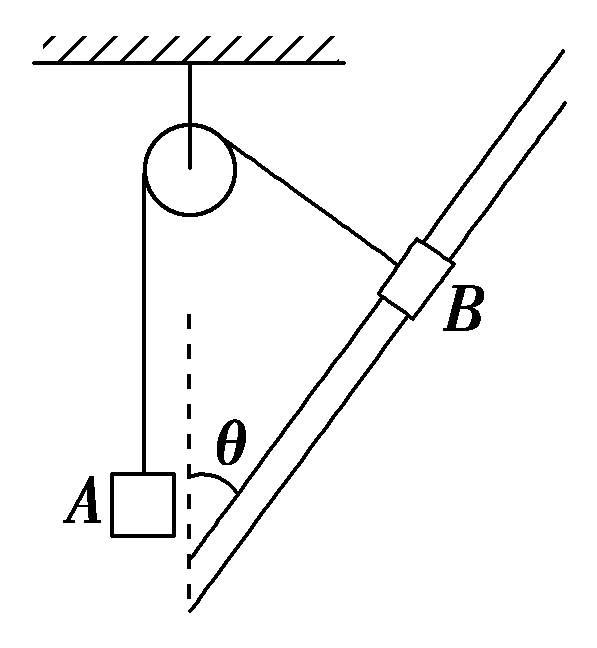
(2020·吉林省实验中学模拟)如图所示,物块A和滑环B用绕过光滑定滑轮的不可伸长的轻绳连接,滑环B套在与竖直方向成θ=37°的粗细均匀的固定杆上,连接滑环B的绳与杆垂直并在同一竖直平面内,滑环B恰好不能下滑,滑环和杆间的动摩擦因数μ=0.4,设滑环和杆间的最大静摩擦力等于滑动摩擦力,则物块A和滑环B的质量之比为( )
A.$\dfrac{5}{7}$ B.$\dfrac{7}{5}$ C.$\dfrac{13}{5}$ D.$\dfrac{5}{13}$
展开答案
【答案】C
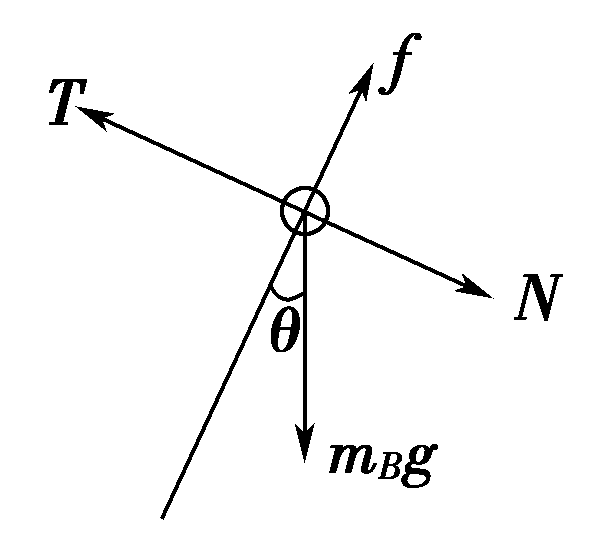
【解析】对A受力分析,根据平衡条件有$T=m_Ag$,活结的重要特点,两边的力是相等的。对B受力分析,如图所示根据平衡条件有由题可知$ m_Bgcos \theta=f,T=N+m_Bgsin \theta$,滑环B 恰好不能下滑,则所受的静摩擦力沿杆向上且达到最大值,有$f=\mu N$,联立解得$$\frac{m_A}{m_B}=\frac{13}{5}$$
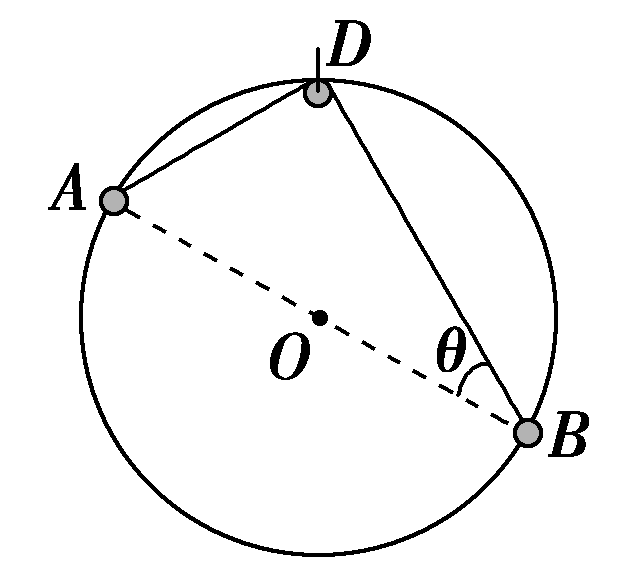
如图所示,竖直放置的光滑圆环,顶端D点处固定一定滑轮(大小忽略),圆环两侧套着质量分别为m1、m2的两小球A、B,两小球用轻绳绕过定滑轮相连,并处于静止状态,A、B连线过圆心O点,且与右侧绳的夹角为θ。则A、B两小球的质量之比为( )
A.$tan\theta$ B.$ \dfrac{1}{tan\theta}$ C. $\dfrac{1}{cos \theta}$ D. $sin\theta ^2$
展开答案
【答案】B
【解析】对两小球分别受力分析,作出力的矢量三角形(正弦定理),如图所示。
对小球A,可得
$$\dfrac{m_1 g}{sin(90-\theta)}=\dfrac{T}{sin a}$$
对小球B,可得
$$\dfrac{m_2 g}{sin \theta}=\dfrac{T}{sin(180- a)}$$
$sin a = sin(180-a)$,$ sina(90-a)=cos a$
$$\dfrac{m_1 g}{m_2 g}=\dfrac{1}{tan \theta}$$
故选B。
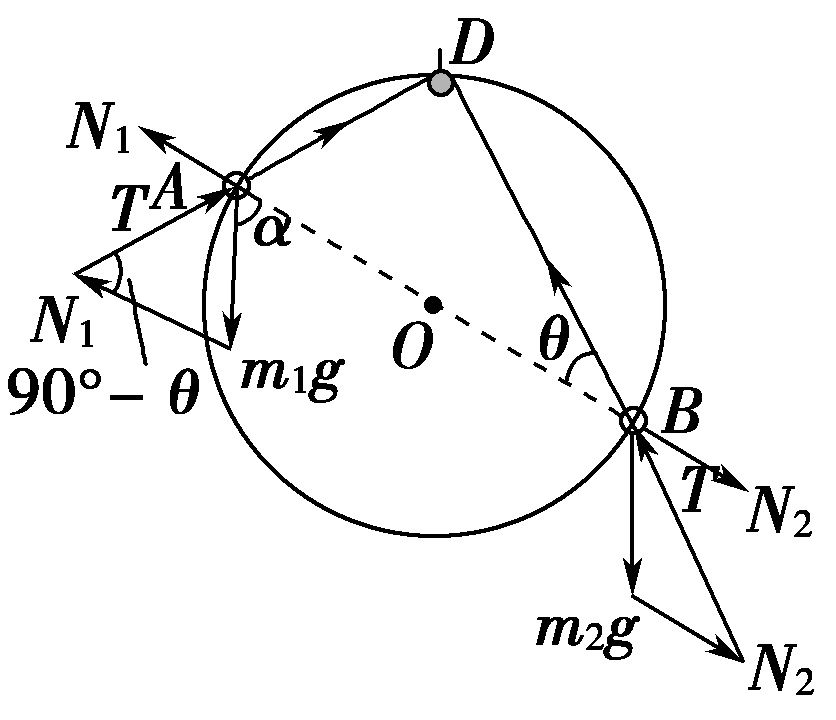
解法2
我们只需连接OD即可,对于那些对三角函数不熟悉的同学,这个方法极好,就是相似三角形法。
$$ \frac{m_a g}{OD} =\frac{T_A}{OA}$$
$$ \frac{m_b g}{OD} =\frac{T_B}{OB}$$
因为$T_B$=$T_A$两个式子直接相除,这个方法经常用到。
$$ \frac{m_b }{m_b} =\frac{OB}{OA}=\frac{1}{tan}$$
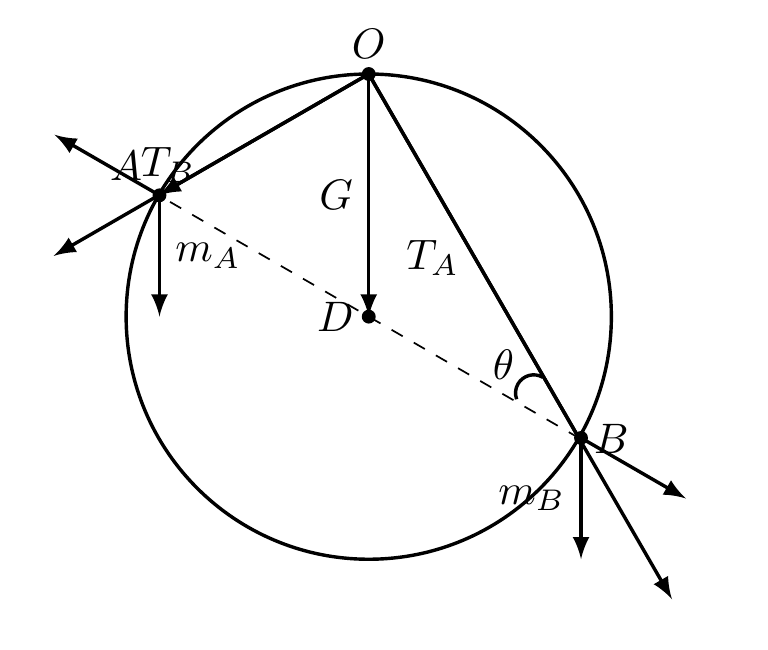
如图所示,物体A、B置于水平地面上,与地面间的动摩擦因数均为0.5,物体A、B用跨过光滑轻质动滑轮的细绳相连,现用逐渐增大的力斜向上提动滑轮,某时刻拉A物体的绳子与水平面成53°角,拉B物体的绳子与水平面成37°角,A、B两个物体仍处于平衡状态,此时若继续增大向上的力,A、B两个物体将同时开始运动,则A、B两个物体的质量之比为(认为最大静摩擦力等于滑动摩擦力,sin 37°=0.6,cos 37°=0.8,g=10 m/s2)
A.$\dfrac{7}{3}$ B.$\dfrac{10}{11}$ C .$\dfrac{9}{7}$ D.$\dfrac{4}{5}$
展开答案
【答案】B
【解析】:对A、B两物体,由于中间是滑轮,所以$F_{TA}$与$F_{TB}$二者相等,这是一个标准的活结扩展题目。
$F_Tcos 53°=\mu(m_Ag-F_Tsin 53°)$,$F_Tcos 37°=μ(m_Bg-F_Tsin 37°)$,解得(讨厌的解得,很多学生因为计算粗心而计算不对,好在这是选择题,可以可以根据选项判断对错,如果是计算题就坏了)$\dfrac{m_a}{m_b}=\dfrac{10}{11}$,选项A、C、D错误,选项B正确.
计算的时候一定要一步一步来。
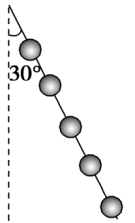
(2020·宁夏银川一中月考)一串小灯笼(五只)彼此用轻绳连接,并悬挂在空中.在稳定水平风力作用下发生倾斜,悬绳与竖直方向的夹角为30°,如图所示.设每个灯笼的质量均为m.则自上往下第一只灯笼对第二只灯笼的拉力大小为( )
A.$2\sqrt{3}mg$ B. $\dfrac{2\sqrt{3}mg} {3}$ C. $\dfrac{8\sqrt{3}mg} {3} $D.8mg
展开答案
【答案】C
【解析】:
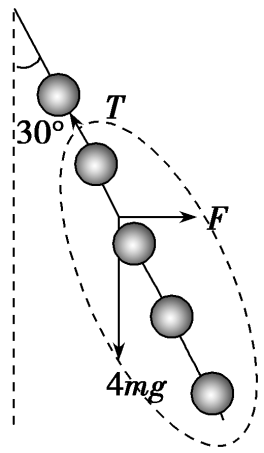
这是一个标准的整体法题目,求第一只灯笼对第二只灯笼的拉力,以下面四个灯笼为研究对象,受力分析如图所示,根据共点力的平衡条件可知拉力
$$T=\frac{4mg}{cos 30}=\frac{8\sqrt{3}mg} {3} $$
故A、B、D错误,C正确.
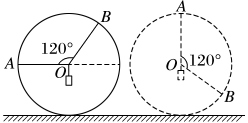
(2020·天一大联考)如图所示,半径为 R 的圆环竖直放置,长度为 R 的不可伸长的轻细绳 OA、OB,一端固定在圆环上,另一端在圆心 O 处连接并悬挂一质量为 m 的重物,初始时 OA 绳处于水平状态.把圆环沿地面向右缓慢转动,直到 OA 绳处于竖直状态,在这个过程中( )
A.OA 绳的拉力逐渐增大
B.OA 绳的拉力先增大后减小
C.OB 绳的拉力先增大后减小
D.OB 绳的拉力先减小后增大
展开答案
【答案】B
【解析】:以重物为研究对象,重物受到重力 mg、OA 绳的拉力 F1、OB 绳的拉力 F2 三个力而平衡,构成矢量三角形,置于几何圆中如图:在转动的过程中,OA 绳的拉力 F1 先增大,转过直径后开始减小,OB 绳的拉力 F2 开始处于直径上,转动后一直减小,A、C、D 错误.故B 正确。
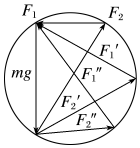
很多学生很难直接看出来这个是怎么得来的,看右侧的两个连续的图,第一步分解完之后,$G$,$F_A$,$F_B$,围成的三角形, 下面大的三角形是完全相似的,所以就会进化成上面那个图,这样我们一眼就能看出变化了。
到这里大家可以看出来,力的分解就是一个几何题目。
多多训练,物理学家从来都是用简单的思维解决最难的问题,一旦你发现哪个问题你听不懂,那只能说明这个理论是错误的。
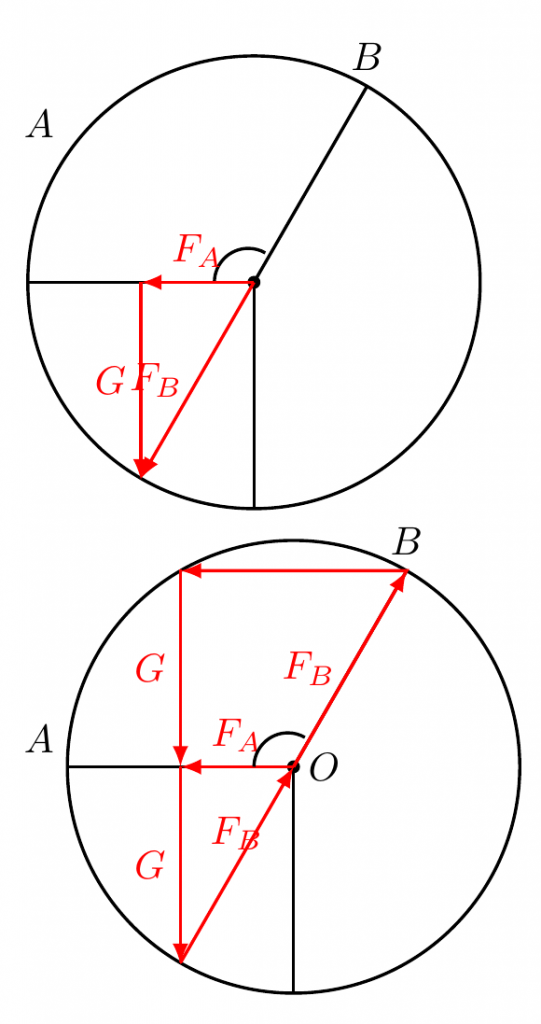
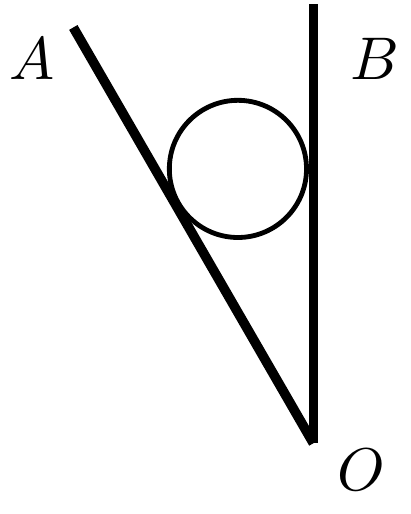
如图,AOB为夹角固定的V形槽,开始时槽板OB位于竖直平面内,光滑小球静置槽中.槽板OA受到的压力为NA,槽板OB受到的压力为NB.在V形槽沿顺时针方向缓慢旋转至OB水平的过程中( )
A.NA逐渐减小,NB逐渐增大
B.NA先增大后减小,NB逐渐增大
C.NA逐渐减小,NB先增大后减小
D.NA先增大后减小,NB先增大后减小
展开答案
【答案】C
【解析】:对球受力分析,重力、AO板支持力,BO板支持力,三力平衡,根据共点力平衡条件,三个力可以构成首位相连的矢量三角形,如图所示:将V形槽沿顺时针方向缓慢旋转至OB水平的过程中,两个支持力的方向顺时针转动90°,等效成重力方向顺时针转动90°,故角θ不变,角α不断变小(锐角),角β不断变大(先锐角后钝角);根据正弦定理,
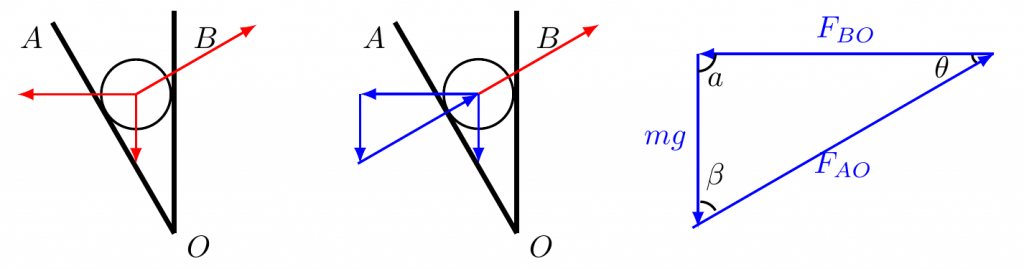
$$\frac{mg}{sin \theta}=\frac{F_{BO}}{sin \beta}=\frac{F_{AO}}{sin a}$$
$$F_{AO}= \frac{sina}{sin \theta}mg$$
$$F_{BO}= \frac{sin \beta}{sin \theta}mg$$
角θ不变,角α不断变小(鋭角),故FAO不断减小;
角θ不变,角β不断变大(先锐角后钝角),故FBO先变大后变小,
根据牛顿第三定律可知,NA不断减小,NB先变大后变小,故C正确.
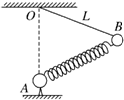
如图所示,A、B两球用劲度系数为k1的轻弹簧相连,B球用长为L的细线悬于O点,A球固定在O点正下方,且O、A间的距离恰为L,此时绳子所受的拉力为F1,现把A、B间的弹簧换成劲度系数为k2的轻弹簧,仍使系统平衡,此时绳子所受的拉力为F2,则F1与F2的大小关系为F1______ F2.(填“大于”、“等于”或“小于”)
展开答案
【答案】等于
解:以小球B为研究对象,分析受力情况,由平衡条件可知,弹簧的弹力N和绳子的拉力F的合力F合与重力mg大小相等,方向相反,即F合=mg,作出力的合成如图,由三角形相似得:
$\frac{F_合}{OA}=\frac{F}{OB}$
又由题,OA=OB=L,得,F=F合=mg,可见,绳子的拉力F只与小球B的重力有关,与弹簧的劲度系数K无关,所以得到:F1=F2;
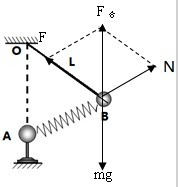
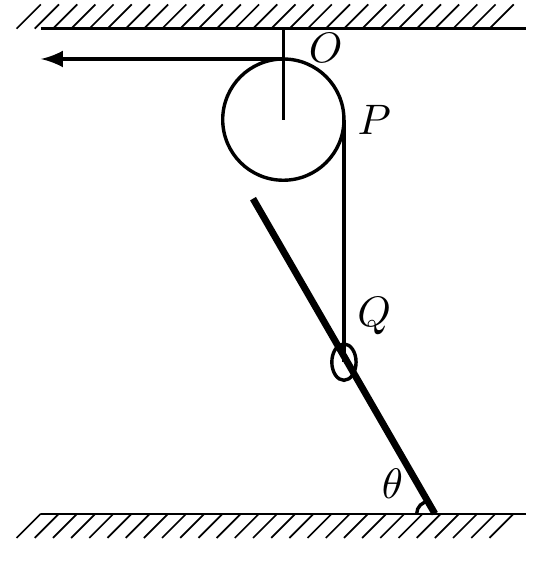
将一光滑轻杆固定在地面上,杆与地面间夹角为θ,一光滑轻环套在杆上,一个大小和质量都不计的光滑滑轮用一条轻绳OP悬挂在天花板上,用另一轻绳通过滑轮系在轻环上,现用手水平向左拉绳,当设法使轻环在杆上某点静止不动时,OP绳与水平方向的夹角为( )
A. 90°
B. 45°
C. θ
D. 45°-$\dfrac{\theta}{2}$
展开答案
【答案】等于
【解析】:只需要想一下,光滑的环会停在什么地方就行了,好好想一下再往下看。
因为没有摩擦力,最终PQ一定会和杆子垂直。这道题的关键就在于此,我们审题的时候一定要抓住平衡,物理最重要的就是平衡,通过平衡可以找到等量关系,可以找到画图的突破点,可以理解能量、动量守恒等等。解题的核心就是找平衡。
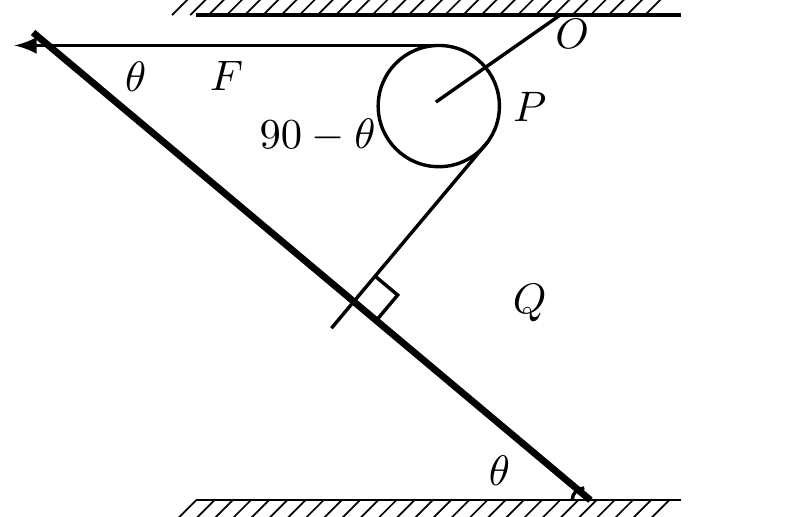
所以 $ \dfrac{90-{\theta}}{2}$ =45°-$\dfrac{\theta}{2}$
如图为汽车内常备的两种类型的“千斤顶”:甲是“菱”形,乙是“Y”形,摇动手柄,使螺旋杆转动,A、B间距离发生改变,从而实现重物的升降.若重物重力均为G,螺旋杆保持水平,AB与BC之间的夹角都为θ,不计杆件自重,则甲、乙两千斤顶螺旋杆的拉力大小之比为( )
A.1∶1 B.1∶2
C.2∶1 D.2∶3
展开答案
【答案】A
【解析】 根据题意,对“Y”形千斤顶B点受力分析如图甲,由平衡条件得$F=\dfrac{G}{tan \theta}$
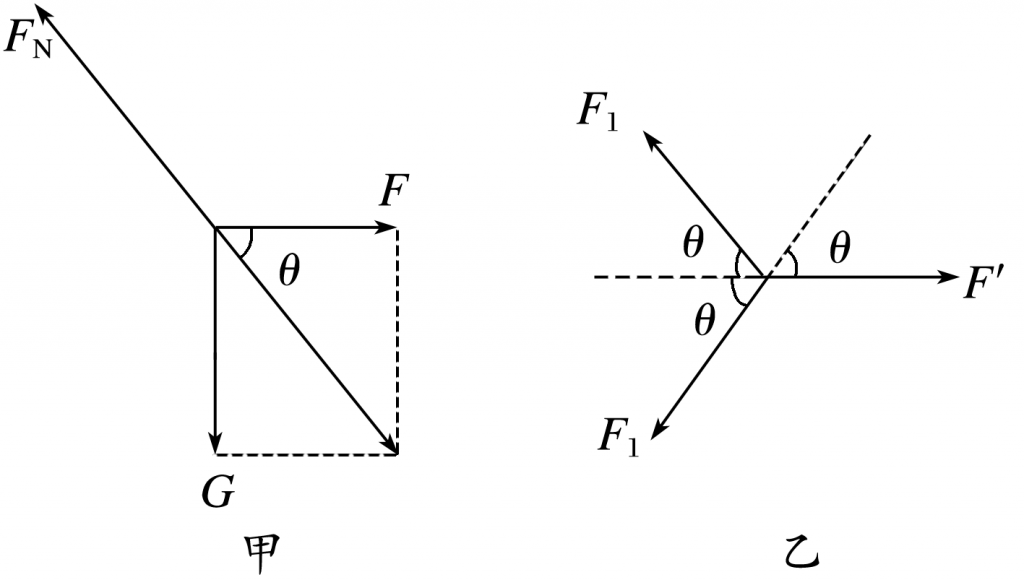
对“菱”形千斤顶C点受到的压力G分解为沿两臂的两个分力,根据对称性可知,两臂受到的压力大小相等,设大小为F1,有2F1sin θ=G,对“菱”形千斤顶B点受力分析如图乙,由平衡条件得F′=2F1cos θ,二者联立解得$F′=\dfrac{G}{tan \theta}$,方程是一种重要的思维方法,非常管用,则甲、乙两千斤顶螺旋杆的拉力大小之比为1∶1.故选A.
一个拱桥模型,左右各三块完全相同的石头,各个接触面完全光滑,试求:$m_3:m_2=?$。
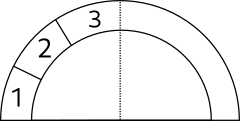
展开答案
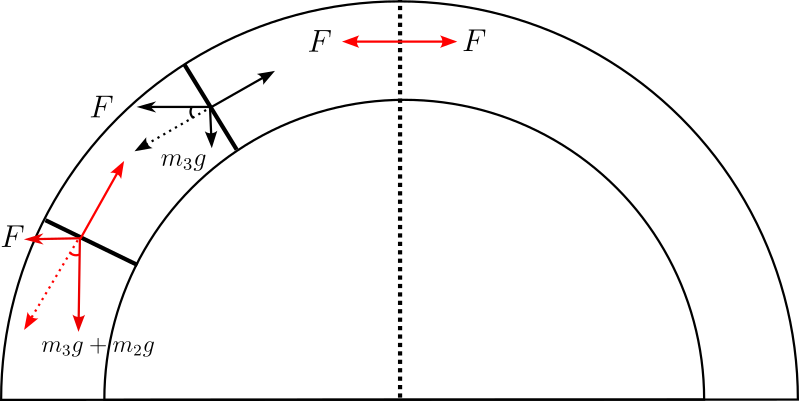
左右两部分的力是相等的!所以可以按照上图分解
$tan30=\dfrac{m_3g}{F}$
$tan60=\dfrac{(m_3+m_2)g}{F}$
解得:$m_3:m_2=1:2$
如图所示,质量为m的物块A被轻质细绳系住斜吊着放在倾角为30°的静止斜面上,物块A与斜面间的动摩擦因数为μ($\mu = \dfrac{\sqrt{3}}{3}$).细绳绕过定滑轮O,左右两边与竖直方向的夹角α=30°、β=60°,细绳右端固定在天花板上,O’为细绳上一光滑动滑轮,下方悬挂着重物B.整个装置处于静止状态,重力加速度为g,认为最大静摩擦力等于滑动摩擦力.
(1)重物B质量为多少时,A与斜面间恰好没有摩擦力?
(2)求在满足(1)问情景时,水平地面对斜面的摩擦力大小?
(3)重物B质量满足什么条件时,物块A不会滑动?
展开答案
(1)分析,先对A进行受力分析,A对斜面恰好没有摩擦力,即$F_f=0$
根据平衡条件有$F_Tsin30°=mgsin30°$ 正交分解并非固定模式,我们把力都在斜面上分解是一样的结果。
解得:$F_T=\dfrac{\sqrt{3}}{3}mg$
再对重物B和华东轮整体分析,根据平衡条件有
$2F_Tcos60°=m_bg$
得$m_b=\dfrac{\sqrt{3}}{3}m$
(2)用整体法,只有$F_T$的力是可以提供摩擦力的。
所以$F_Tsin30°=F_f$
$F_f=\dfrac{\sqrt{3}}{6}m$
(3)如果A物体恰好不上滑,则对A平行斜面方向
$F_{T1}cos30°-mgsin30°-F_{f1}=0$
垂直斜面方向:$F_{N1}+F_{T1}sin30°-mgcos30°=0$
得$F_{T1}=\dfrac{(1+\sqrt{3}\mu)mg}{\sqrt{3}+\mu}$
如果物体A恰好不下滑,摩擦力反向,则对A平行斜面方向:$F_{T2}cos30°-mgsin30°+F_{f2}=0$
垂直斜面方向:$F_{N2}+F_{T2}sin30°-mgcos30°=0$
得$F_{T1}=\dfrac{(1-\sqrt{3}\mu)mg}{\sqrt{3}-\mu}$
$\dfrac{(1-\sqrt{3}\mu)mg}{\sqrt{3}-\mu} \eqslantless m_b \eqslantless\dfrac{(1+\sqrt{3}\mu)mg}{\sqrt{3}+\mu}$
【例】(2020·安徽庐巢七校联盟第三次联考)如图甲所示, A、B两小球通过两根轻绳连接并悬挂于O点,已知两轻绳OA和AB的长度之比为$\sqrt{3}$:1,A、B两小球质量分别为2m和m,现对A、B两小球分别施加水平向右的力F1和水平向左的力F2,两球恰好处于如图乙的位置静止,此时B球恰好在悬点O的正下方,轻绳OA与竖直方向成30°,则( )
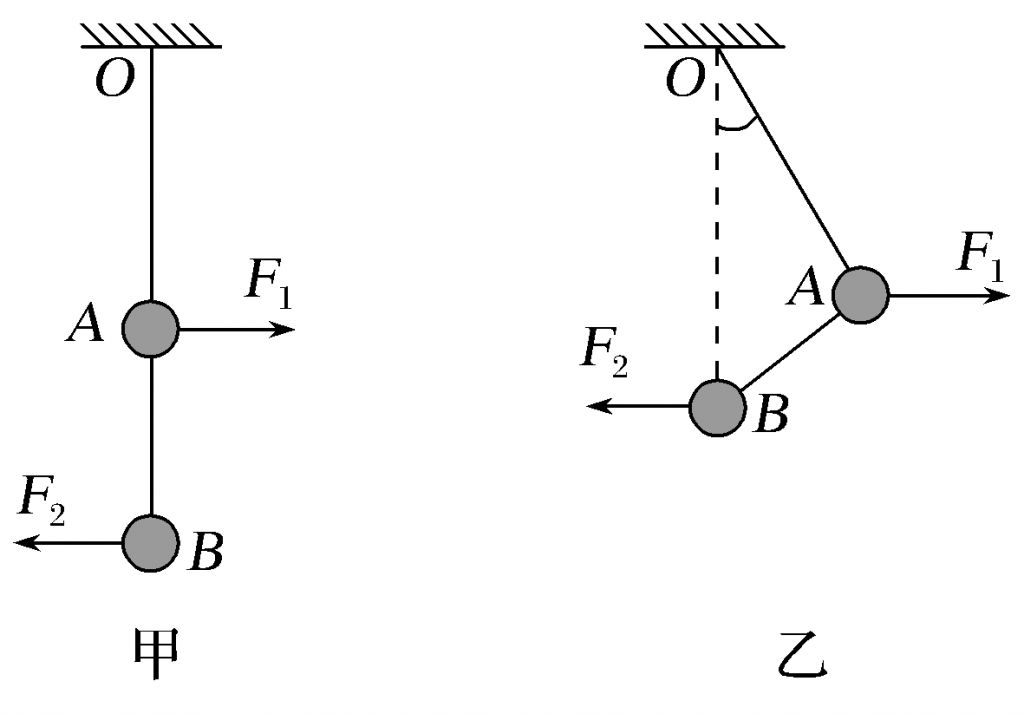
A.F1=F2 B.F1=$\sqrt{3}$ F2 C.F1=2F2 D.F1=3F2
展开答案
【解析】 由题意知两轻绳OA和AB的长度之比为$\sqrt{3}$∶1,B球恰好在悬点O的正下方,由几何关系可知,OA与AB垂直;以B球为研究对象,受力示意图如图甲所示,由平衡条件得
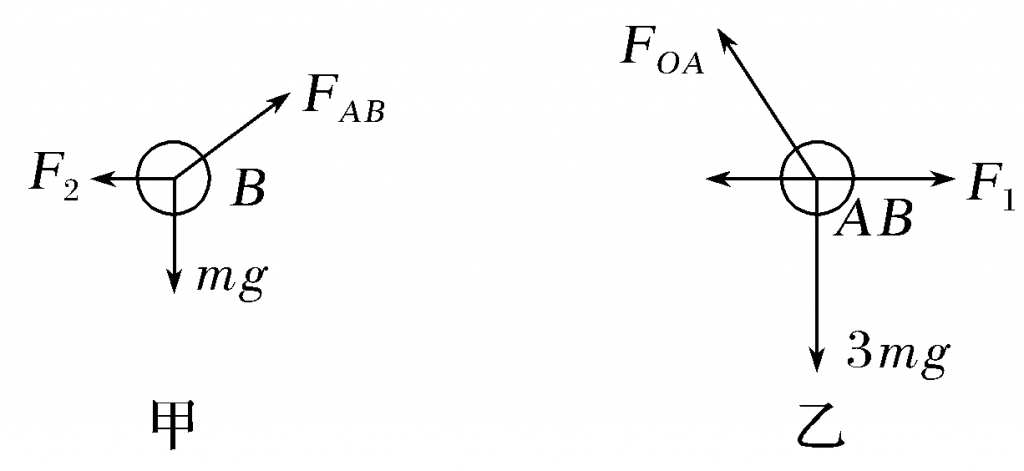
F2=mgtan(90°-30°)=$\sqrt{3}$mg
以A、B两球整体为研究对象,受力示意图如图乙所示,由平衡条件得
F1-F2=3mgtan 30°=$\sqrt{3}$mg
可得F1=2$\sqrt{3}$mg,即F1=2F2,故C正确。
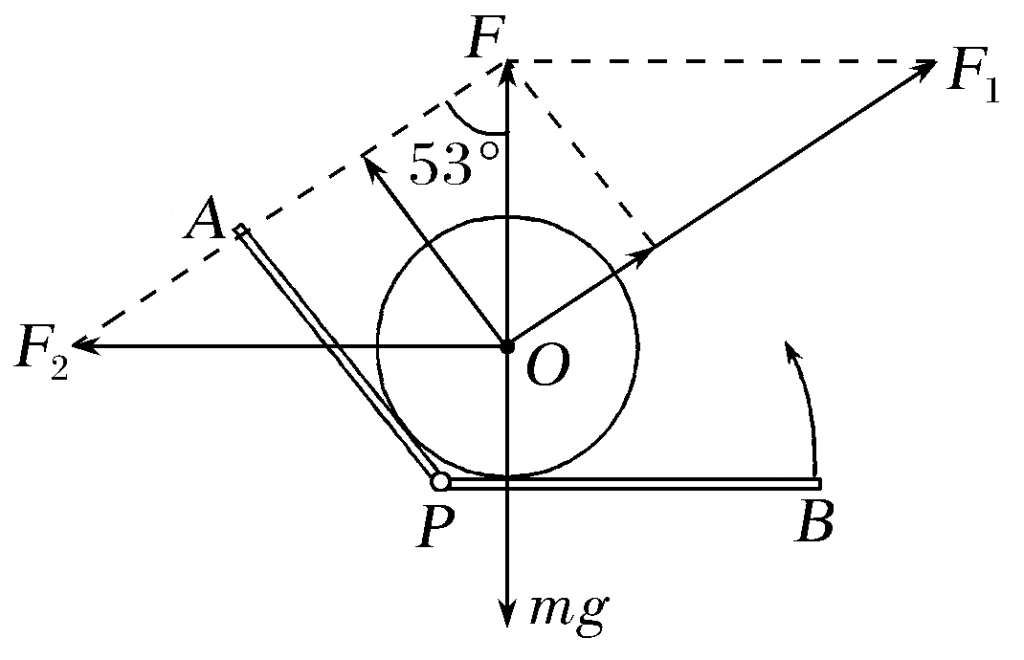
【例】(2021·广东汕头市第一次模拟)如图所示,足够长的光滑平板AP与BP用铰链连接,平板AP与水平面成53°角固定不动,平板BP可绕水平轴在竖直面内自由转动,将一均匀圆柱体O放在两板间。在使BP板由水平位置缓慢转动到竖直位置的过程中,下列说法正确的是( )
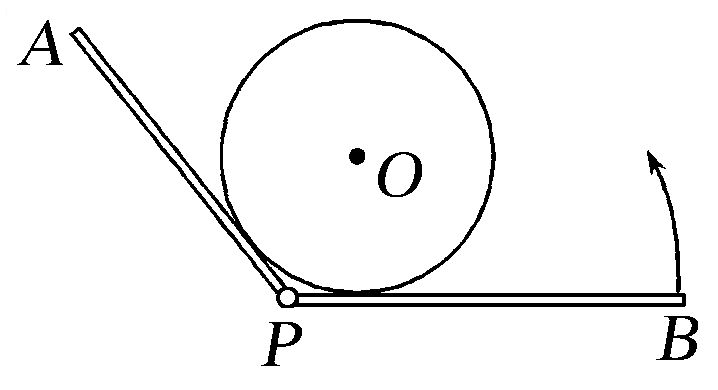
A.当BP沿水平方向时,BP板受到的压力最大
B.当BP沿竖直方向时,AP板受到的压力最大
C.当BP沿竖直方向时,BP板受到的压力最小
D.当BP板与AP板垂直时,AP板受到的压力最小
展开答案
【答案】 B
【解析】 小球一直处于平衡状态,三个力中的任意两个力的合力与第三个力等值、反向、共线,故F1和F2的合力F一定与重力等值、反向、共线。所以画图时一定要保持重力的长度不变,其他两个力始终在同一个参考系中,这样就可以很方便从图中可以看出力的变化,F1越来越大,F2先变小,后变大,到竖直位置时,F2>mg,故选项B正确,A、C、D错误。
如图所示,三个质量为10N的球在处于稳定状态,求地面受到的摩擦力?

展开答案
(2021·1月重庆市学业水平选择性考试适应性测试,7)如图所示,垂直墙角有一个截面为半圆的光滑柱体,用细线拉住的小球静止靠在接近半圆底端的M点。通过细线将小球从M点缓慢向上拉至半圆最高点的过程中,细线始终保持在小球处与半圆相切。下列说法正确的是( )
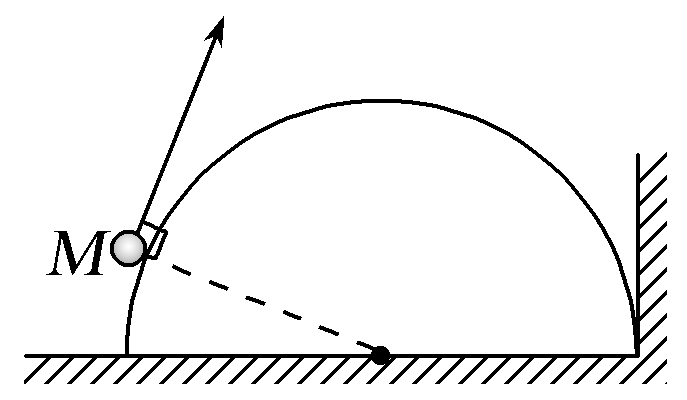
A.细线对小球的拉力先增大后减小
B.小球对柱体的压力先减小后增大
C.柱体受到水平地面的支持力逐渐减小
D.柱体对竖直墙面的压力先增大后减小
展开答案
【答案】 D
【解析】 以小球为对象,设小球所在位置沿切线方向与竖直方向夹角为θ,沿切线方向有
$F_T=mgcos \theta$
沿半径方向有
$F_N=mgsin \theta$
通过细线将小球从M点缓慢向上拉至半圆最高点的过程中θ 增大,所以细线对小球的拉力减小,小球对柱体的压力增大,故A、B错误;以柱体为对象,竖直方向有
$F_地=Mg+F_Nsin \theta=Mg+mg sin \theta ^2$
水平方向有
$F_墙=F_N cos \theta=mg sin \theta cos \theta=\frac{1}{2}mgsin 2\theta$
θ 增大,柱体受到水平地面的支持力逐渐增大;柱体对竖直墙面的压力先增大后减小,当θ=45°时柱体对竖直墙面的压力最大,故D正确。这个函数经常出现。
跳伞运动员练习跳伞时,从悬停在空中的直升机上打开降落伞竖直跳下,跳离直升机后,由于受到水平风力的作用,最后斜向下匀速落向地面。则在匀速落向地面的过程中,伞和运动员()
A.所受空气作用力方向斜向上
B.所受空气作用力方向竖直向上
C.重力势能减少量大于机械能减少量
D.重力势能减少量等于机械能减少量

展开答案
【答案】BD
一般来说作用力是指的整体的力
