变压器电能的传输
如图所示为远距离输电的原理图.发电厂输出的电压恒定,升压、降压变压器均为理想变压器。由于用户负载的变化会造成其得到的电压变化,供电部门要实时监控,监控电表为理想电表。若某次监侧发现$V_2$表的示数减小,则下列判断正确的是
A. 电流表A1的示数增大 B. 电流表A2的示数减少
C. 电压表V1的示数增大 D. 输电线损失的功率减小
展开答案
【答案】
【解析】A、C、发电厂输出的电压恒定,升压变压器的匝数比不变,所以电压表$V_1$的示数不变,由于某次监测发现$V_2$表的示数减小,降压变压器的匝数比不变,则降压变压器的输入电压变小,又由于$U_1$不变,所以输电线路上损失的电压增大,$U_损=I_1R$,则电流表$A_1$的示数增大,故A正确,C错误;
B、由于电流表$A_1$的示数增大,降压变压器的匝数比不变,所以降压变压器副线圈中电流增大,即电流表$A_2$的示数增大,故B错误;
D、由于电流表$A_1$的示数增大,根据$P_损=I_1^2R$可知,输电线损失的功率增大,故D错误。
一含有理想变压器的电路如图所示,图中电阻$R_0$为定制电阻,R为可变电阻,Ⓐ为理想交流电流表,U为正弦交流电源,输出电压的有效值U恒定。当可变电阻R的阻值为$2R_0$时,电流表的示数为I;当可变电阻R的阻值为$11R_0$时,电流表的示数为$\dfrac{1}{5}I$。则该变压器原、副线圈匝数比为( )
A、5 B、4 C、3 D、2
展开答案
【答案】D
【解析】:当然这个题目有很多解决方案,最好还是先找到等式在什么地方,然后下手,下面就是做题的基本原理。
$\dfrac{U-IR_0}{n}=nI2R_0$
$\dfrac{U-\dfrac{I}{5}R_0}{n}=nI11R_0$
解得:$n=2$ ,所以选D
如图所示,变压器输入的交变电压$u=220\sqrt{2}sin100 \pi t(V)$,副线圈匝数可调,电阻$R=100Ω$,$L_1$、$L_2$均是额定电压为20V,额定功率为20W的小灯泡,通过调节副线圈的匝数,使S闭合前后,$L_1$均能正常发光,则S闭合前后副线圈的匝数之比为( )
A.1:11 B. 2:1
C. 3:5 D. 6:11
展开答案
【答案】D
【解析】由变压器输入的交变电压为:$u=220\sqrt{2}sin100 \pi t(V)$,可知有效值为:$U_1=220V$,S闭合前是$L_1$与R串联,$L_1$正常发光可知其额定电流为:$I=\dfrac{P}{U}=\dfrac{20}{20}A=1A$,故有:$U_2=IR+U=1\times100+20=120V$由变压器原理可知:$\dfrac{n_1}{n_2}=\dfrac{U_1}{U_2}=\dfrac{11}{6}$;
S闭合后$L_1$和$L_2$并联后再与R串联,有:$U’=2IR+U=220V$同样可得:$\dfrac{n_1}{n_2′}=\dfrac{U_1}{U_2′}=\dfrac{1}{1}$;
联立可解得:$\dfrac{n_2}{n_1}=\dfrac{6}{11}$
某同学设计了一个充电装置,如图所示,假设永磁铁的往复运动在螺线管中产生近似正弦式交流电,周期为0.2s,电压最大值为0.05V,理想变压器原线圈接螺线管,副线圈接充电电路,原、副线圈匝数比为1∶60,下列说法正确的是( )
A、 交流电的频率为10Hz
B、 副线圈两端电压最大值为3V
C、 变压器输入电压与永磁铁磁场强弱无关
D、 充电电路的输入功率大于变压器的输入功率
展开答案
【答案】B
【解析】
A、学习物理一定要根据物理现象理解定义,并且用数学的方式写下来,比如:频率一秒多少次,周期一次多少秒,在圆周运动中
$T=\dfrac{2\pi}{\omega}$一圈需要的时间
$f=\dfrac{1}{T}$一秒时间内转了多少圈。
所以:$f=\dfrac{1}{0.2}=5Hz$
B、由理想变压器原理可知$\dfrac{u_1}{u_2}=\dfrac{n_1}{n_2}$
副线两端的最大电压为${u_2}=\dfrac{n_2}{n_1}u_1=0.05v \times 60=3 v$
C.根据法拉第电磁感应定律可知,永磁铁磁场强,线圈中产生的感应电动势越大,变压器的输入电压会越大,C不符合题意;
D.由理想变压器原理可知,充电电路的输入功率等于变压器的输入功率,D不符合题意。
如图所示,虚线是正弦交流电的图像,实线是另一交流电的图像,它们的周期T和最大值$U_m$相同,则实线所对应的交流电的有效值U满足( )
A、$U=\dfrac{1}{2}U_M$
B、$U=\dfrac{\sqrt{2}}{2}U_M$
C、$U>\dfrac{\sqrt{2}}{2}U_M$
D、$U<\dfrac{\sqrt{2}}{2}U_M$
展开答案
【答案】D
【解析】 正弦交流电的有效值$U_有=\dfrac{U}{\sqrt{2}}$
如图,发电机的矩形线圈长为2L、宽为L,匝数为N,放置在磁感应强度大小为B的匀强磁场中,理想变压器的原、副线圈匝数分别为$n_0$、$n_1$和$n_2$,两个副线圈分别接有电阻$R_1$和$R_2$,当发电机线圈以角速度$\omega$匀速转动时,理想电流表读数为I,不计线圈电阻,下列说法正确的是( )
A. 通过电阻$R_2$的电流为$\dfrac{n_1I}{n_2}$
B. 电阻$R_2$两端的电压为$\dfrac{n_2IR_1}{n_1}$
C. $n_0$与$n_1$的比值为$\dfrac{\sqrt{2}NBL^2\omega}{IR_1}$
D. 发电机的功率为$\dfrac{\sqrt{2}NBL^2\omega I(n_1+n_2)}{n_0}$
展开答案
【答案】BC
【解析】这类题的核心是能量守恒和$\dfrac{n_1}{n_2}=\dfrac{U_1}{U_2}$
A、对于推导能力不强的同学来说,很可能是因为书写的格式不整齐造成的。
$\dfrac{U_0}{n_0}=\dfrac{U_1}{n_1}$ —— $U_1=\dfrac{U_0 n_1}{n_0}$
$\dfrac{U_0}{n_0}=\dfrac{U_1}{n_2}$—— $U_2=\dfrac{U_0 n_2}{n_0}$
整理:$\dfrac{U_1}{U_2}=\dfrac{n_1}{n_2}$
$U_2=\dfrac{n_2}{n_1}U_1=\dfrac{n_2IR_1}{n_1}$
故而通过$R_2$的电流$I_2=\dfrac{U_2}{R_2}=\dfrac{n_2IR_1}{n_1R_2}$
所以B正确A错误
交流电电动势最大值$E_m=NBS\omega=NB(L\times 2L)\omega$,交流电动势的有效值$E_有=\dfrac{E_m}{\sqrt{2}}=\dfrac{2NBL^2\omega}{\sqrt{2}}=\sqrt{2}NBL^2\omega$
由变压器的变压比得$\dfrac{n_0}{n_1}=\dfrac{E_有}{U_1}=\dfrac{\sqrt{2}NBL^2\omega}{IR_1}$
$R_1$消耗的功率$p_{R1}=I^2R_1$消耗的功率$p_{R2}=I_2^2 R_2=dfrac{U_2}{R_2}=(\dfrac{n_2IR_1}{n_1R_2})^2R_2$
$P_总=p_{R1}+p_{R2}=I^2R_1+(\dfrac{n_2IR_1}{n_1R_2})^2R_2$
特高压输电可使输送中的电能损耗和电压损失大幅降低.我国已成功掌握并实际应用了特高压输电技术.假设从
A处采用550Kv的超高压向B处输电,输电线上损耗的电功率为$\Delta P$,到达B处时电压下降了$\Delta U$.在保持A处输送的电功率和输电线电阻都不变的条件下,改用1100Kv特高压输电,输电线上损耗的电功率变为$\Delta P’$,到达B处时电压下降了$\Delta U’$.不考虑其他因素的影响,则( )
A.$\Delta P’=\dfrac{1}{4}\Delta P$
B.$\Delta P’=\dfrac{1}{2}\Delta P$
C.$\Delta U’=\dfrac{1}{4}\Delta U$
D.$\Delta U’=\dfrac{1}{2}\Delta U$
展开答案
【答案】AD
【解析】发电厂输出的功率是恒定的,所以电压提高一倍之后,电流减少一半!!!!!
$550Kv \times I=1100Kv \times I’$
所以电流之比为2:1
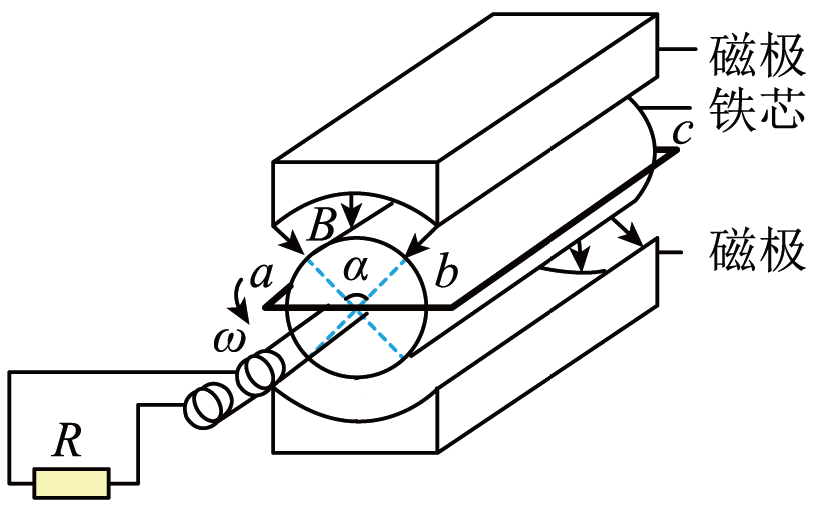
(2012·江苏·高考真题)某兴趣小组设计了一种发电装置,如图所示. 在磁极和圆柱状铁芯之间形成的两磁场区域的圆心角a均为$\dfrac{4}{9}\pi$,磁场均沿半径方向. 匝数为N 的矩形线圈abcd 的边长ab =cd =$1l$、bc =ad=$2l$
. 线圈以角速度ω绕中心轴匀速转动,bc和ad 边同时进入磁场. 在磁场中,两条边所经过处的磁感应强度大小均为B、方向始终与两边的运动方向垂直. 线圈的总电阻为r,外接电阻为R. 求:
(1)线圈切割磁感线时,感应电动势的大小$E_m$;
(2)线圈切割磁感线时,bc 边所受安培力的大小F;
(3)外接电阻上电流的有效值I.
展开答案
【详解】(1)bc、ad边的运动速度 $v=\omega\dfrac{l}{2}$
感应电动势$E_m=4NBlv$.
解得$E_m=2NBl^2ω$
(2)电流 $I_m=\dfrac{E_m}{r+R}$
安培力$F=2NBI_ml$
解得. $F=\dfrac{4N^2B^2l^3\omega}{r+R}$
(3)一个周期内,通电时间$t=\dfrac{4}{9}T$
R上消耗的电能$W=I_m^2Rt$且$W=I_m^2RT$
解得 $I=\dfrac{4NBI^2\omega}{3(r+R)}$
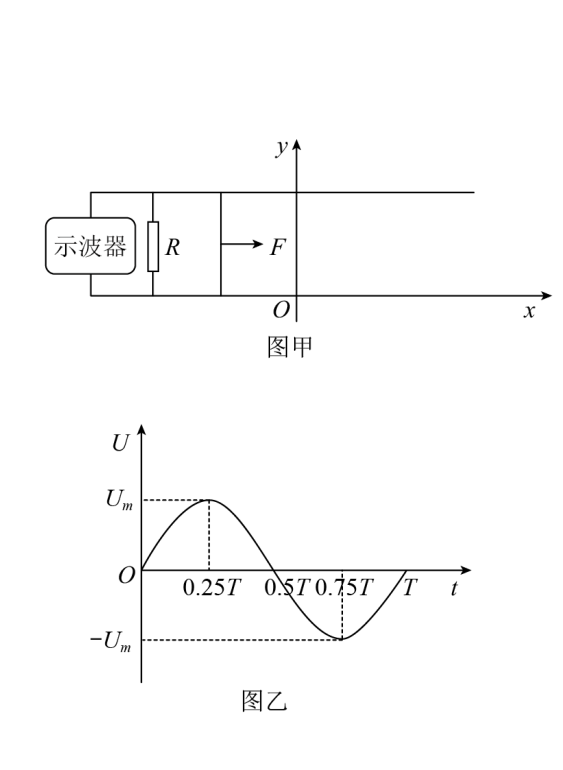
(2020·浙江·高考真题)如图甲所示,在XOY水平面内,固定放置着间距为$l$的两平行金属直导轨,其间连接有阻值为R的电阻,电阻两端连接示波器(内阻可视为无穷大),可动态显示电阻R两端的电压。两导轨间存在大小为B、方向垂直导轨平面的匀强磁场。t-0时一质量为m、长为$l$的导体棒在外力$F$作用下从$x=x_0$。位置开始做简谐运动,观察到示波器显示的电压随时间变化的波形是如图乙所示的正弦曲线。取$x_0=-\dfrac{U_mT}{2\pi Bl}$,则简谐运动的平衡位置在坐标原点O。不计摩擦阻力和其它电阻,导体棒始终垂直导轨运动。(提示:可以用F-x图象下的“面积”代表力F所做的功)
(1)求导体棒所受到的安培力$F_A$随时间t的变化规律;
(2)求在0至0.25T时间内外力$F$的冲量;
(3)若t-0时外力$F_0=1,l=1m,T=2\pi s,m=1kg.R=1\Omega,U_m=0.5V,B=0.5T$,求外力与安培力大小相等时棒的位置坐标和速度。
展开答案
【详解】(1)由显示的波形可得
$U=U_m sin\dfrac{2\pi}{T}t$
$I=\dfrac{U_m}{R} sin\dfrac{2\pi}{T}t$
安培力随时间变化规律:
$F_A=-BIl=-\dfrac{BIU_m}{R} sin\dfrac{2\pi}{T}t$
(2)安培力的冲量:
$I_A=-BI\Delta q$
$\Delta q=\dfrac{Blx_0}{R}$
由动量定理,有:
$I_F+I_A=mv_m$
解得:$I_F=\dfrac{BIU_mT}{2\pi R}+\dfrac{mU_m}{BI}$
(3)棒做简谐运动,有:
$F_A+F=-kx$
当$F_A=-F$时:
$x=0$
$v=\pm v_m=\pm 1m/s$
当$F_A=-F$时,设$X=X’,V=V’$
$F_A=-\dfrac{1}{2}kx’$
$F_0=-kx_0$
$2x’=V’$
根据动能定理:
$\dfrac{1}{2}mv’=\dfrac{1}{2}k(x_0^2-x’^2)$
解得:$x_1’=\dfrac{1}{\sqrt5}m$和$v_1’=\dfrac{2}{\sqrt5}m/s$;
$x_2’=\dfrac{1}{\sqrt5}m$和$v_3’=\dfrac{2}{\sqrt5}m/s$
