万有引力与航天例题
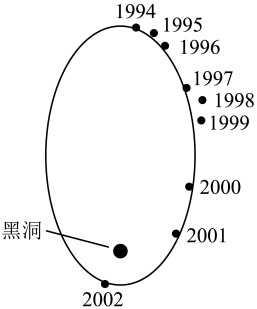
(2021·全国高考真题)科学家对银河系中心附近的恒星S2进行了多年的持续观测,给出1994年到2002年间S2的位置如图所示。科学家认为S2的运动轨迹是半长轴约为1000AU(太阳到地球的距离1AU)的椭圆,银河系中心可能存在超大质量黑洞。这项研究工作获得了2020年诺贝尔物理学奖。若认为S2所受的作用力主要为该大质量黑洞的引力,设太阳的质量为M,可以推测出该黑洞质量约为( )
A.$4\times 10^4M$ B.$4\times10^6M$ C.$4\times10^8M$ D .$4\times10^{10}M$
展开答案
【答案】B
【关键能力】根据万有引力提供向心力推导出太阳的质量及黑洞的质量,模型构建能力,建立S2绕黑洞球做圆周运动的模型。
可以近似把S2看成匀速圆周运动,由图可知,S2绕黑洞的周期T=16年,地球的公转周期T0=1年,S2绕黑洞做圆周运动的半径r与地球绕太阳做圆周运动的半径R关系是
计算一定要注意格式的重要性!!!!
$r=1000R$
根据万有引力等于离心力
$G\dfrac{Mm}{R^2}=mR\omega^2=mR(\dfrac{2\pi}{T})^2$
可以获得一个关于质量的推导式
$M=\dfrac{4\pi^2R^3}{GT^2}$
太阳的质量:$M=\dfrac{4\pi^2R^3}{GT_0^2}=\dfrac{4\pi^2 1^3}{G1^2}$
黑洞的质量:$M_H=\dfrac{4\pi^2 1000^3}{G16^2}$
$M_H=3.96\times 10^6M$
2021·广东高考)2021年4月,我国自主研发的空间站“天和”核心舱成功发射并入轨运行,若核心舱绕地球的运行可视为匀速圆周运动,已知引力常量,由下列物理量能计算出地球质量的是( )
A.核心舱的质量和绕地半径
B.核心舱的质量和绕地周期
C.核心舱的绕地角速度和绕地周期
D.核心舱的绕地线速度和绕地半径
展开答案
【答案】D
【解析】根据核心舱做圆周运动的向心力由地球的万有引力提供,可得
$G\dfrac{Mm}{r^2}=m\dfrac{v^2}{r}=m\omega^2r=m\dfrac{4\pi^2}{T^2}r$
可得质量的关系式,然后去找哪些是已知,哪些是未知即可。
$M=\dfrac{v^2r}{G}=\dfrac{\omega^2 r^3}{G}=\dfrac{4\pi^2 r^3}{GT^2}$
可知已知核心舱的质量和绕地半径、已知核心舱的质量和绕地周期以及已知核心舱的角速度和绕地周期,都不能求解地球的质量;若已知核心舱的绕地线速度和绕地半径可求解地球的质量。
(2021·全国高考真题)2021年2月,执行我国火星探测任务的“天问一号”探测器在成功实施三次近火制动后,进入运行周期约为1.8×105s的椭圆形停泊轨道,轨道与火星表面的最近距离约为2.8×105m。已知火星半径约为3.4×106m,火星表面处自由落体的加速度大小约为3.7m/s2,则“天问一号”的停泊轨道与火星表面的最远距离约为( )
A.6×105m B.6×106m C.6×107m D.6×108m
展开答案
【答案】C
【解析】忽略火星自转则
$\dfrac{GMm}{R^2}=mg$①
可知
$GM=gR^2$
设与为1.8×105s的椭圆形停泊轨道周期相同的圆形轨道半径为r,由万引力提供向心力可知
$$\dfrac{GMm}{r^2}=m\dfrac{4\pi^2}{T^2}r$②
设近火点到火星中心为
$R_1=R+d_1$③
设远火点到火星中心为
$R_2=R+d_2$④
由开普勒第三定律可知
$\dfrac{r^3}{T^2}=\dfrac{(\dfrac{R_1+R_2}{2})^3}{T^2}$⑤
由以上分析可得
$d_2=6$\times 10^7m$
太空中的两颗小行星(S星和N星)的运动可视为在同一平面内沿相同方向绕太阳做匀速圆周运动,测得两小行星之间的距离$\Delta r$随时间变化的关系如图所示。已知S星距太阳的距离大于N星距太阳的距离,仅考虑两小行星与太阳之间的引力。则关于S星和N星的说法正确的是
A.S星的轨道半径为3r
B.S星与N星的周期比为$2\sqrt{2}:1$
C.S星与N星的线速度之比比为$1:\sqrt{3}$
D.S星的角速度为$\dfrac{2\sqrt{2}}{2\sqrt{2}-1}\cdot\dfrac{2\pi}{T}$
展开答案
【答案】 AB
【解析】理解题目中运动的情形是关键点!解决任何第一眼看不懂的题,就是先别套用任何公式,先把运动的状态,轨迹描述出来。
$r_S-r_N=1.5r$
$r_S+r_N=4.5r$
解得:$r_S=3r$、$r_N=1.5r$ A正确
由$\dfrac{T_S^2}{T_N^2}=\dfrac{r_S^3}{r_N^3}$ 解得:$\dfrac{T_S}{T_N}=2\sqrt{2}$,B正确
由$v=\dfrac{GM}{r}$,故S星和N星的线速度之比$1:\sqrt{2}$,C错误
俩行星连续两次距离最近的时间间隔为T,即$\dfrac{T}{T_N}-\dfrac{T}{T_S}=1$,解得$T_S=(2\sqrt{2}-1)T$,所以S星的角速度为$\omega=\dfrac{2\pi}{T_S}=\dfrac{2\pi}{(2\sqrt{2}-1)T}$,D错误
假设地球可视为质量均匀分布的球体,已知地球表面的重力加速度在两极的大小为g0,在赤道的大小为g;地球自转的周期为T,引力常数为G,则地球的密度为( )
A.$\dfrac{3\pi}{GT^2}\dfrac{g_0-g}{g_0}$ B.$\dfrac{3\pi}{GT^2}\dfrac{g_0}{g_0-g}$ C.$\dfrac{3\pi}{GT^2}$ D.$\dfrac{3\pi}{GT^2}\dfrac{g_0}{g_0}$
展开答案
【答案】B
【解析】很多学生做不对这种题,主要原因流程问题。即便理解了重力产生的原理,还是要看计算的流程,通过流程才能解决细心问题,否则很难作对。
$mg_0=G\dfrac{Mm}{R^2}$ $\Rightarrow$ $M=\dfrac{g_0R^2}{G}$
$mg=G\dfrac{Mm}{R^2} – \omega^2 Rm=mg_0 – (\dfrac{2\pi}{T})^2 Rm$
做这种题目一定要注意顺序
$mg_0 – mg = (\dfrac{2\pi}{T})^2 Rm$
$g_0 – g = (\dfrac{2\pi}{T})^2 R$
$\dfrac{g_0 – g}{\dfrac{4\pi^2}{T^2}} =R$
$\dfrac{T^2(g_0 – g)}{4\pi^2} =R$
$\rho=\dfrac{M}{V}$
训练一下看看 能不能算出答案
据《当代天文学》11月17日报道,被命名为“开普勒11145123”的恒星距离地球5000光年,其赤道直径和两极直径仅相差6千米,是迄今为止被发现的最圆天体.若该恒星的体积与太阳的体积之比约为k1,该恒星的平均密度与太阳的平均密度之比约为k2,则该恒星表面的重力加速度与太阳表面的重力加速度之比约为( )
A、$\sqrt[3]{K_1}\cdot K_2$ B、$\sqrt[3]{K_1^2}\cdot K_2$ C、$\dfrac{k_2}{\sqrt[3]{K_1}}$ D、$\dfrac{k_2}{\sqrt[3]{K_1^2}}$
展开答案
【答案】A
【解析】由
$G\dfrac{Mm}{R^2}=mg$
有
$g=G\dfrac{M}{R^2}=G \dfrac{\rho \cdot \dfrac{4}{3}\pi^2 R^3}{R^2}=\dfrac{4}{3}G \rho \pi R$
体积$V=\dfrac{4}{3}\pi R^3$得
$g=\dfrac{4}{3}G \rho \pi \sqrt[3]{\dfrac{3V}{4\pi}}$
该恒星的表面重力加速度与太阳的表面重力加速度之比为
$\dfrac{g_恒}{g_太}=\dfrac{\rho_恒}{\rho_太} \sqrt[3]{\dfrac{V_恒}{V_太}}=\sqrt[3]{K_1}\cdot K_2$
如图所示,O为地球球心,A为地球表面上的点,B为O、A连线间的点,AB=d,将地球视为质量分布均匀的球体,半径为R.设想挖掉以B为圆心、以$\dfrac{d}{2}$为半径的球.若忽略地球自转,则挖出球体后A点的重力加速度与挖去球体前的重力加速度之比为( )
A.$1-\dfrac{d}{4R}$ B.$1-\dfrac{d}{7R}$
C.$1-\dfrac{d}{R}$ D.$\dfrac{d}{R-d}$
展开答案
【答案】B
【解析】本题采用割补法,设想没有挖掉以B为圆心、以$\dfrac{d}{2}$为半径的球,则A点物体所受的引力是以B为圆心、以$\dfrac{d}{2}$为半径的球的引力和剩余部分的引力的矢量和,设地球质量为M,以B为圆心、以$\dfrac{d}{2}$为半径的球的质量为M1,则
$M=\rho \dfrac{4}{3}\pi R^3$ , $M_1=\rho \dfrac{4}{3}\pi (\dfrac{d}{2})^3$
根据万有引力定律,有:
$F=\dfrac{GMm}{R^2}=\dfrac{4\pi \rho GRm}{3}$ ,$F_1=\dfrac{GM_1m}{d^2}=\dfrac{\pi \rho Gdm}{6}$
所以$F_剩=F-F_1=\dfrac{4\pi \rho GRm}{3}-\dfrac{\pi \rho Gdm}{6}$
所以
根据牛顿第二定律得:挖出球体后A点的重力加速度与挖去球体前的重力加速度之比为:
$\dfrac{g_剩}{g}=\dfrac{4R-d/2}{4R}=1-\dfrac{d}{8R}$
如图所示,双星系统由质量不相等的两颗恒星组成,质量分别是M、m(M>m), 他们围绕共同的圆心O做匀速圆周运动.从地球A看过去,双星运动的平面与AO垂直,AO距离恒为L.观测发现质量较大的恒星M做圆周运动的周期为T,运动范围的最大张角为△θ(单位是弧度).已知引力常量为G,△θ很小,可认为sin△θ= tan△θ= △θ,忽略其他星体对双星系统的作用力.则( )
A.恒星m的角速度大小为$\dfrac{2\pi}{T}\sqrt{\dfrac{M}{m}}$
B.恒星m的轨道半径大小为$\dfrac{ML\Delta\theta}{2m}$
C.恒星m的线速度大小为$\dfrac{\pi ML\Delta\theta}{mT}$
D.两颗恒星的质量m和M满足关系式$\dfrac{m^3}{(m+M)^2}=\dfrac{\pi^2(L\Delta\theta)^3}{2GT^2}$
展开答案
【答案】BCD
【解析】
A错误,恒星P与Q具有相同的角速度,则角速度为$\omega=\dfrac{2\pi}{T}$
B正确,恒星P的轨道半径$R=Ltan\dfrac{\Delta\theta}{2}=\dfrac{1}{2}L\Delta\theta$,因为双星系统,$m\omega^2r=M\omega^2R$,解恒星的半径大小为$r=\dfrac{ML\Delta\theta}{2m}$
C正确恒星
D正确 $G\dfrac{Mm}{(r+R)^2}=M\omega^2R=m\omega^2r$解得
$GM=\omega^2r(r+R)^2$
$Gm=\omega^2R(r+R)^2$
得到$G(M+m)\omega^2(r+R)^3$ 结合$m\omega^2r=M\omega^2R$
联立$\dfrac{m^3}{(m+M)^2}=\dfrac{\pi^2(L\Delta\theta)^3}{2GT^2}$
