万有引力与航天

---

1、这一部分的内容只遵循一个物理现象，那就是离心力等于向心力！

F=am 是解决一切圆周运动的核心，天体运动只需要降低自由度，把椭圆变成圆周运动即可，半长轴当长半径即可！

$G\dfrac{Mm}{R^2}=\dfrac{v^2}{R}m$

其他的各种物理量都可以通过这个平衡关系得到！需要注意的是m是会被消掉的。

关系：$v=\omega R$

线速度和周期的关系$v=\dfrac{2\pi R}{T}$

角速度周期的关系：$\omega=\dfrac{2\pi}{T}$

---

---

估算中心天体的质量和密度的两条思路

（1）利用中心天体的半径和表面的重力加速度g计算．

由$G\dfrac{Mm}{R^2}=mg$求出$M=\dfrac{gR^2}{G}$

进而求得$\rho=\dfrac{M}{V}=\dfrac{M}{\dfrac{4}{3}\pi R^3}=\dfrac{3g}{4\pi GR}$

(2)利用环绕天体的轨道半径r和周期T计算．

由$G\dfrac{Mm}{R^2}=m\dfrac{4 \pi^2}{T^2}r$，可得出$M=\dfrac{4\pi^2 r^3}{GT^2}$

$\rho=\dfrac{M}{V}=\dfrac{M}{\dfrac{4}{3}\pi R^3}=\dfrac{3\pi r^3}{GT^2R^3}$

若环绕天体绕中心天体表面做匀速圆周运动，轨道半径r＝R

则$\rho=\dfrac{3\pi}{GT^2}$

---

---

1.线速度：$G\dfrac{Mm}{r^2}=m\dfrac{v^2}{r}$⇒ $v=\sqrt{\dfrac{GM}{r}}$   

2.角速度：$G\dfrac{Mm}{r^2}=m\omega^2r$⇒ $\omega=\sqrt{\dfrac{GM}{r^3}}$

3.周期：$G\dfrac{Mm}{r^2}=m(\dfrac{2\pi}{T})^2r$⇒ $T=2\pi \sqrt{\dfrac{r^3}{GM}}$

4.向心加速度：$G\dfrac{Mm}{r^2}=ma$⇒ $a=\dfrac{GM}{r^2}$

结论：r越大，v、ω、a越小，T越大。

---

---

1.变轨原理

(1)为了节省能量，在赤道上顺着地球自转方向发射卫星到圆轨道Ⅰ上。如图所示。

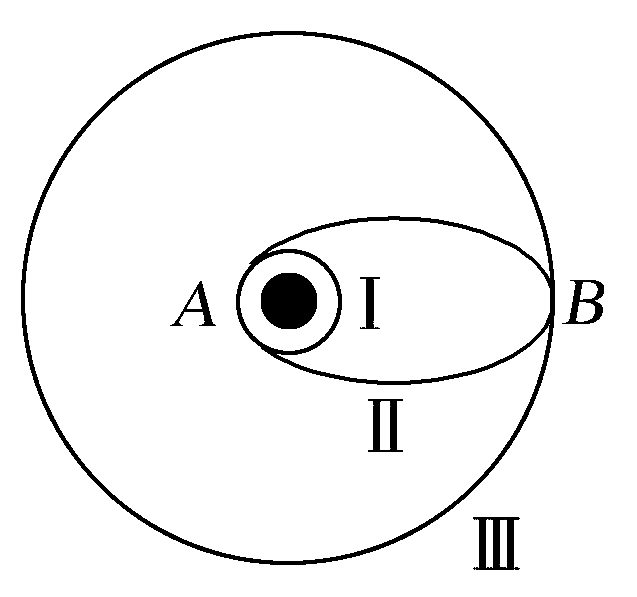
(2)在A点(近地点)点火加速，由于速度变大，万有引力不足以提供卫星在轨道Ⅰ上做圆周运动的向心力，卫星做离心运动进入椭圆轨道Ⅱ。

(3)在B点(远地点)再次点火加速进入圆形轨道Ⅲ。

2.变轨过程分析

(1)速度：设卫星在圆轨道Ⅰ和Ⅲ上运行时的速率分别为v₁、v₃，在轨道Ⅱ上过A点和B点时速率分别为v_A、v_B。在A点加速，则v_A＞v₁，在B点加速，则v₃＞v_B，又因v₁＞v₃，故有v_A＞v₁＞v₃＞v_B。

(2)加速度：因为在A点，卫星只受到万有引力作用，故不论从轨道Ⅰ还是轨道Ⅱ上经过A点，卫星的加速度都相同；同理，卫星在轨道Ⅱ或轨道Ⅲ上经过B点的加速度也相同。

(3)周期：设卫星在Ⅰ、Ⅱ、Ⅲ轨道上的运行周期分别为T₁、T₂、T₃，轨道半径分别为r₁、r₂(半长轴)、r₃，由开普勒第三定律$\dfrac{r^3}{T^2}$可知T₁＜T₂＜T₃。

(4)机械能：在一个确定的圆(椭圆)轨道上机械能守恒。若卫星在Ⅰ、Ⅱ、Ⅲ轨道的机械能分别为E₁、E₂、E₃，则E₁＜E₂＜E₃。

---

---

1.相同点

(1)都以地心为圆心做匀速圆周运动。

(2)同步卫星与赤道上的物体具有相同的角速度。

2.不同点

(1)向心力不同

同步卫星、近地卫星均由万有引力提供向心力，$\dfrac{GMm}{r^2}=\dfrac{mv^2}{r}$；而赤道上的物体随地球自转做圆周运动的向心力(很小)是万有引力的一个分力，$\dfrac{GMm}{r^2}\neq \dfrac{mv^2}{r}$。

(2)向心加速度不同

比较项目	卫星绕地球运行的向心加速度	物体随地球自转的向心加速度(不局限于赤道)
产生原因	由万有引力产生	由万有引力的一个分力(另一分力为重力)产生
方向	指向地心	垂直且指向地轴
大小	$a=\dfrac{GM}{r^2}$(地面附近a近似等于g)	$a=r\omega^2$，r为地面上某点到地轴的距离，ω为地球自转的角速度
特点	随卫星到地心的距离的增大而减小	从赤道到两极逐渐减小