简单机械功和功率例题
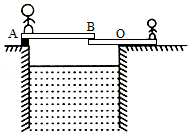
一个600N重的成年人和一个小孩都要过一道5m宽的水渠。成人从左岸到右岸,而小孩从水渠右岸到左岸,两岸各有一块4m长的坚实木板,他们想出右图所示的方式过渠。请分析在忽略木板自身重量和木板叠交距离的情况下,要使成年人和小孩都能平安过渠,小孩的体重不能轻于多少牛?( )
A.100N B.200N C.300N D.400N
展开答案
【解答】解:(1)因成年人较重,所以只要成年人能安全过水渠,则小孩也能安全过水渠;小孩站在B′处让成年人先从木板上过水渠,当成年人到达水渠对岸后,站在B′处,然后再让小孩过水渠如图所示:
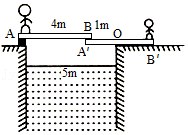
(2)把木板A′B′视为杠杆,O为支点,成年人对A′B′的压力视为阻力F2,小孩对木板的压力视为动力F1,当成年人在A′时,阻力(成年人对A′B′的压力)最大,为F2=G成年人=600N,由题意和图示可知:OA′=1m,OB′=3m,由杠杆平衡条件可得:F1×OB′=F2×A′O,则$F_1=\dfrac{F_2×OA’}{OB’}=\dfrac{600N×1m}{3m}=200n$,
即小孩的体重不能轻于200N;
故选:B
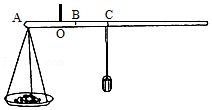
如图是一副称量准确的杆秤示意图,秤砣质量为1kg,秤杆和秤盘总质量为O.5kg,定盘星B到提纽O的距离OB为2cm,秤盘到提纽O的距离OA为10cm。若有人换了一个质量为0.8kg的秤砣,实际质量3kg的物品,让顾客误以为得到物品的质量是多少( )
A.3.8kg B.3.6kg C.3.96kg D.3.75kg
展开答案
【解答】解:设秤杆和秤盘的重心为D,当杠杆平衡时秤砣放在B点,
因为G秤×OD=G砣×OB,即:m秤g×OD=m砣g×OB,
0.5kg×OD=1kg×2cm,
所以OD=4cm,
使用1kg秤砣(正常情况下),设秤砣到O点的距离L,
因为m物g×OA+m秤g×OD=m砣g×L 即:3kg×g×10cm+0.5kg×g×4cm=1kg×g×L,
解得:L=32cm,
即OC=L=32cm;
秤杆上标定的质量值与标定的质量值位置到定盘星B点的距离的关系是$\dfrac{3kg}{OC-OB}=\dfrac{3kg}{32cm-2cm}=0.1kg/cm$;
当使用0.8kg秤砣时,秤量3kg的质量时,秤砣到O点的距离设为OE,
因为m物g×OA+m秤g×OD=m砣′g×OE,
即:3kg×g×10cm+0.5kg×g×4cm=0.8kg×g×OE,
解得:OE=40cm;
此时E位置标定的质量值m=0.1kg/cm×(OE﹣OB)=0.1kg/cm×(40cm﹣2cm)=3.8kg。
则实际3千克的物品会让顾客误以为质量为3.8kg,故A正确,BCD错误。
故选:A。
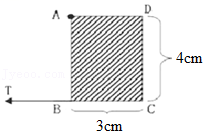
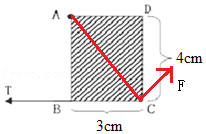
(2017•武侯区校级自主招生)如图所示,一块长3cm、宽4cm的质量不计的矩形薄板ABCD可绕过A点的固定轴在纸面内无摩擦地自由转动,现过B点沿CB方向对板施加T=9N的拉力作用,为使板保持静止,需要在板上的某一处施加另一个在纸面内的拉力F(未画出),其大小由F的作用位置和方向决定,在所有可能情况中,F的最小值为( )
A.4.5N B.7.5N C.7.2N D.9.0N
展开答案
【解答】解:
由题知,A为支点;过B点沿CB方向对板施加T=9N的拉力,则拉力T的力臂为AB=4cm=0.04m,
由图知,当另一拉力F作用在C点,且其力臂为AC时,F的力臂最大,
由杠杆平衡条件可知,拉力F的值最小,
由勾股定理可得:$AC=\sqrt{AD^2+DC^2}=\sqrt{(0.03m)^2+(0.04)^2}=0.05m$,
由杠杆平衡条件可得:T×AB=F×AC,
即:9N×0.04m=F×0.05m。
解得F=7.2N。
故选:C。
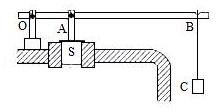
如图所示是锅炉保险阀门的示意图。当阀门受到的蒸汽压力超过其安全值时,阀门就会被拉开。如OB=2m,OA=0.5m,阀门的底面积S=2cm2,锅炉内气体压强的安全值p=6×105Pa,则B所挂的重物G是______25N(杠杆的重力,摩擦均不计)。
展开答案
【解答】解:由$p=\dfrac{f}{s}$得,气体产生的向上的力:
F1=p1S=6×105Pa×2×10﹣4m2=120N,
大气产生的向下的压力为:F2=p2S=1×105Pa×2×10﹣4m2=20N,
则阀门受到的向上的力为:F=F1﹣F2=120N﹣20N=100N;
根据杠杆的平衡条件可知,F•OA=G•OB,
所以物体的重力:$G=\dfrac{F×OA}{OB}=\dfrac{100N×0.5m}{2m}=25N$。
故答案为:25。
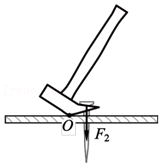
如图所示,使用羊角锤拔钉子,请在图中画出最省力时的动力臂和用力方向。
展开答案
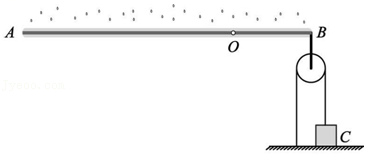
如图为一个简易雨量测试仪,质量均匀的直杆AB外均匀包裹着海绵,直杆与干海绵的总质量为1.5kg,且可绕垂直纸面的转轴O转动,OA:OB=7:3,杆右端B点连接一个质量不计的滑轮,绕在滑轮上的细绳一端固定在地面上,另一端系在质量为1kg的重物C上。晴天时,直杆AB呈水平状态,重物静止在地面上。g取10N/kg,求:
(1)晴天时,重物C对地面的压力是多大
(2)雨天时,海绵均匀吸收雨水,吸收多少质量的雨水,直杆开始绕O点旋转
展开答案
【解答】解:(1)设直杆长为10L0,直杆与干海绵重心在其几何中心,距B端长为5L0,O为支点,故直杆与干海绵重力的力臂(阻力力臂)为:
L2=5L0﹣3L0=2L0,阻力G=mg=1.5kg×10N/kg=15N,
动力臂L1=3L0,
根据杠杆的平衡条件:
G×2L0=FB×3L0,
$F_B=\dfrac{2L_0}{3L_0}×G=\dfrac{2}{3}×15N=10N$;
由力的作用是相互的,杆对绳子的拉力为10N,即绳子对滑轮向上的拉力为10N,因有两段绳子分担10N的拉力,由力的平衡,故与C相连的绳子对C竖直向下的拉力大小为:$T=\dfrac{10N}{2}=5N$,由力的相互性,绳子对C竖直向上的拉力大小为:T′=5N,故重物C对地面的压力:
F压=GC﹣T′=mCg﹣T=1kg×10N/kg=10N﹣5N=5N;
(2)设吸收质量为m′的雨水,直杆开始绕O点旋转,
则阻力F2′=(m′+1.5kg)g,
动力为:FB′=2GC=2×1kg×10N/kg=20N,
根据杠杆的平衡条件:
F2′×2L0=FB′×3L0,
即(m′+1.5kg)g×2L0=20N×3L0,
吸收雨水的质量:m′=1.5kg时直杆开始绕O点旋转。
答:(1)晴天时,重物C对地面的压力是5N;
(2)雨天时,海绵均匀吸收雨水,吸收1.5kg的雨水,直杆开始绕O点旋转。
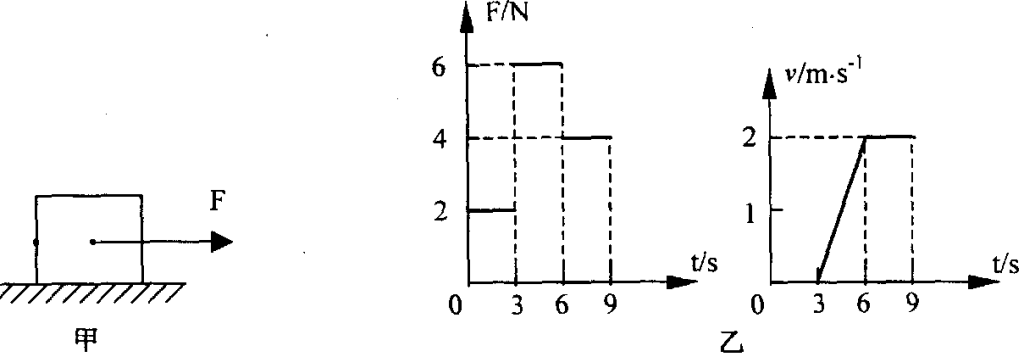
如图甲所示, 水平地面上的一物体,受到方向不变的水平推力F的作用, F的大小与时间t的关系和物体速度v与时间t的关系如图乙所示, 则第2秒末时,物体处于__________状态, 第6秒末到第9秒末, 推力F做功是_________焦耳
展开答案
【答案】静止 24
如图甲所示, 带有滑轮的物体A放置在粗糙水平地面上, 质量为m的电动机固定在物体A上, 通过滑轮水平匀速拉动物体A, 物体A移动速度为v甲, 移动距离为s甲, 电动机做功为W1, 电动机的功率为P1, 对绳的拉力为T1, 电动机收绳速度为v1;如图乙所示, 将电动机固定在地面上, 使电动机通过滑轮水平匀速拉动物体A, 物体A移动速度为v乙,移动距离为s乙, 电动机做功为W2, 电动机的功率为P2, 对绳的拉力为T2, 电动机收绳速度为v2.已知地面粗糙程度相同, s甲=s乙 , P1=P2, 不计绳重及滑轮与轴的摩擦.则下列判断正确的是

A.T1<T2 B.W1> W2 C.v1>v2 D.v甲>v乙
展开答案
【答案】B
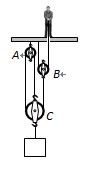
如图所示, 质量为70kg的小刚站在高台上通过滑轮组匀速提升货物,提升货物的质量为100kg.已知滑轮A、B的质量均为4kg, 滑轮C的质量为8kg, 绳重及滑轮的摩擦均可忽略不计, g取10N/kg. 关于小刚提升货物过程中.滑轮组的机械效率约为 _______
展开答案
【答案】83.3%
$\eta=\dfrac{Gh}{Gh+G_Ch+G_B3h}=\dfrac{1000N}{1000N+80N+3\times40N}=83.3$ %
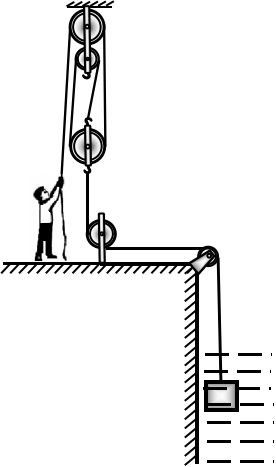
工人用滑轮组提升水中物体A, 如图所示.当物体A完全在水面下被匀速提升的过程中, 工人对绳子竖直向下的拉力为F1, 水平地面对工人的支持力为N1;滑轮组的机械效率η1为60%. 当物体A完全打捞出水面后被匀速提升的过程中, 滑轮组的机械效率为η2, 工人对绳子竖直向下的拉力为F2, 水平地面对工人的支持力为N2. 已知工人所受重力为500N, N1∶N2=7∶2;物体A所受重力为1000N.不计绳重、滑轮与轴的摩擦以及水的阻力, g取10N/kg.求:
(1)动滑轮所受重力G动;
(2)物体A的密度ρA;
(3)滑轮组的机械效率η2;
(4) 当物体A完全在水面下时, 以0.1m/s的速度被匀提升时, 人拉绳的功率P1.
展开答案
【答案】(1)250N; (2)1.6×103kg/m3(3)80% (4)62.5w
(1)以工人为研究对象, 进行受力分析如图1甲、乙所示.
工人处于静止状态, 所以有:
G人=F′1+N1 即:N1=G人-F′1—-①
G人=F′2+N2 N2=G人-F′2—-②
—————--(甲、乙受力分析图或方程正确得1分)
当物体A浸没在水中时, 动滑轮与物体A的受力情况如图2(A)所示.
当物体A完全露出水面时, 动滑轮与物体A的受力情况如图2(B)所示.
由(A)图: 3F1=GA+G动-F浮—-③
由(B)图: 3F2=GA+G动—-④
—–((A)、(B)受力分析图或方程正确得1分)
∵F1¢=F1, F2¢=F2
∴N1/N2=(G人-F1)/(G人-F2)=7/2 —-⑤
又∵η1=W有/W总=(GA-F浮)/ 3F1=60% —-⑥
将③、④式代入⑤、⑥式, 将G人=500N, GA=1000N代入,
解得:G动=250N—————————–(1分)
(2)由⑥式得:60%=(GA-F浮) / (GA+G动-F浮)
=(1000N-F浮) / (1000N+250N-F浮)
解得:F浮=625N —————(1分)
∵F浮=ρ水gVA∴VA=F浮/ρ水g
∴ρA= m/VA = GA/gVA=(GA /F浮)·ρ水
=(1000N /625N) ×1.0×103kg/m3
=1.6×103kg/m3 ———–(1分)
(3)∵η2=W′有/W′总
=GA/ (GA+G动)
=1000N/(1000N+250N) [来源:学_科_网Z_X_X_K]
=80% ————(1分)
(4) ∵P1=F1· v1
=( GA+G动-F浮) /3 × 3 vA
= (1000N+250N-625N )×0.1m/s
=62.5W———————–(1分)
阅读短文,回答问题。
载人飞艇 2024 年 3 月 30 日,我国自主研制的“祥云”AS700 载人飞艇成功完成首飞。某飞艇如图甲所示,其气囊体积巨大,采用轻质材料制作。飞艇升空靠浮力来实现,水平飞行靠发动机提供动力。发动机输出的能量用于做推动功和辅助功:推动功指克服空气阻力推动飞艇水平飞行做的功;辅助功指发动机驱动飞艇上发电机工作所做的功,辅助功的功率恒定。
当飞艇低速($v\leq12 m/s$)水平直线飞行时,其受到的空气阻力$F_{阻}$与速度$v$的关系如图乙所示。飞艇部分参数见下表。忽略气囊厚度及气囊外其他部分受到的浮力。
| 参数 | 数值 |
|---|---|
| 空载质量(不含氦气) | 3750 kg |
| 气囊总容积 | 4200 \(m^{3}\) |
| 发动机额定输出功率 | \(3×10^{5}\) W |
| 辅助功的功率 | \(5×10^{4}\) W |
| 发动机效率 | 36% |
| 最大速度 | 70 km/h |
(1)气囊采用轻质材料制作是为了减小_______;
(2)飞艇的发电机利用_______的原理发电;
(3)将气囊充满氦气,此时飞艇受到的浮力为_______N,飞艇最多可载 _______位乘客升空;(每位乘客质量$m = 60$ kg,$\rho_{空气}=1.2$ kg/$m^{3}$,$\rho_{氦气}=0.2$ kg/$m^{3}$,$g$取 10 N/kg)
(4)飞艇先后以 3 m/s 和 6 m/s 的速度水平匀速直线飞行相同的时间,推动功分别为$W_{1}$和$W_{2}$,则$W_{1}:W_{2} =$ _______;
(5)飞艇低速水平匀速直线飞行时,若消耗 10 kg 燃油,可飞行的最大距离为 _______。(燃油的热值$q_{油}=4.5×10^{7}$ J/kg)
(攀枝花中考试题)如图所示,在水平路面上行驶的汽车通过滑轮组拉着重为G=9×104N的货物A沿斜面向上匀速运动,货物A的速度为V=2m/s,经过t=10s,货物A竖直升高h=10m,已知对绳子的拉力F的功率P=120kw,不计绳、滑轮的质量和摩擦,求:
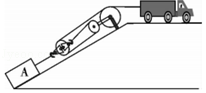
(1)t时间内汽车对绳的拉力所做的功;
(2)汽车对绳的拉力大小;
(3)斜面的机械效率。
展开答案
【答案】 (1)\(1.2\times10^{6}J\) (2)\(20000N\) (3)\(75\%\)。
【解析】 (1)由\(W = Pt\)可得\(10s\)内汽车对绳的拉力所做的功\(W = Pt = 1.2\times10^{5}W\times10s = 1.2\times10^{6}J\)。
(2) 货物匀速直线运动时,\(10s\)内移动的距离\(s = vt = 2m/s\times10s = 20m\)。,
根据\(W = Fs\)可得汽车对绳的拉力大小
\(F=\frac{W}{s}=\frac{1.2\times10^{6}J}{60m}=20000N\)。
(3) 由图知,滑轮组对绳子的拉力\(F_{拉}=3F_{车}=3\times20000N = 60000N\)
斜面做的有用功
\(W_{有}=Gh = 9\times10^{4}N\times10m = 9\times10^{5}J\),
斜面做的总功
\(W_{总}=F_{拉}s = 60000N\times20m = 1.2\times10^{6}J\)
则斜面的机械效率
\(\eta=\frac{W_{有}}{W_{总}}\times100\%=\frac{9\times10^{5}J}{1.2\times10^{6}J}\times100\% = 75\%\)。
如图所示,吊篮的重力为400N,动滑轮总重力为50N,定滑轮总重力为40N,人的重力为600N,不计绳重与摩擦,人在吊篮里拉着绳子不动时需用力( )
A.218N
B.220N
C.210N
D.236N
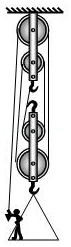
展开答案
【解答】解:将人、吊篮、动滑轮看作一个整体,由于他们处于静止状态,受力平衡。
则人的拉力$F=\dfrac{1}{5}(400N+50N+600N)=210N$。
故选:C。
