浮力经典例题
如图所示, 底面积为200cm2的容器底部有一固定轻质弹簧, 弹簧上方连有一边长为10cm的正方体木块A, 当容器中水深为20cm时, 木块A有$\dfrac{2}{5}$的体积浸在水中, 此时弹簧恰好处于自然状态, 没有发生形变. 向容器内缓慢加水, 当弹簧伸长了1cm时停止加水, 此时弹簧对木块拉力为1N. 加水前后容器底部受到水的压强变化了_______Pa. (不计弹簧受到的浮力, g取10N/kg)

展开答案
【答案】200
分析:弹簧伸长了1cm,物体受到的浮力也增大了1N, 物体多浸入液体1cm,则液体总共要上升的1cm+1cm=2cm.
如图甲所示的圆柱形容器中装有适量的某种液体,现将密度为0.6×103kg/m3的正方体木块A放入容器中,木块静止时露出液面的体积与浸人液体的体积之比为1:3;在木块上表面轻放一个物块B(VA=2VB),A的上表面刚好与液面相平,如图乙所示。若将物块B单独放人此液体中,它静止时将( )
A.悬浮 B.漂浮 C.沉底 D.无法判断
展开答案
【答案】B
假设A的体积为200cm3,那B的体积是100cm3
根据浮力=重力,$\rho_液 S_A 3=\rho_A S_A 4$
$\rho_液=0.8g/cm3$
那么增加的浮力就是重力$0.8g/cm3 x50cm3=40g$
$\rho_B=\dfrac{40g}{100cm3}=0.4g/cm3$
如图所示,两只相同的气球,分别充入氢气和空气,充气后体积相同,放飞气球时只有氢气气球升上空中。若它们在空气中受到的浮力分别为 F氢和F空,则下列说法中正确的是
A.F 氢>F 空 B.F 氢=F 空
C.F 氢<F 空 D.条件不足,无法比较
展开答案
【答案】B
【解析】根据阿基米德原理,即$/rho g v_排$进行判断。
两只相同的气球,分别充入氢气和空气,充气后体积相同,排开空气的体积相同,空气密度相同,排开空气的体积相同时,浮力相等。
如图甲所示,水平桌面上盛满水的容器中放有一个钢珠。把木块轻轻放入容器中,木块静止时如图乙所示。以下说法正确的是
A.钢珠不受浮力作用
B.木块受到的浮力大于钢珠受到的浮力
C.两图中容器对桌面的压强相等
D.两图中水对容器底的压强不相等
展开答案
【答案】C
两图中容器对桌面的压力等于容器、水和物体的总重力;
杯子中有一个漂浮的盒子,如果我沉在水底的小石球拿起来,放倒盒子里,盒子依然漂浮,请问液面会如何变化()
A、上升
B、下降
C、不变
D、无法确定
展开答案
【答案】B
如图,某装有水的容器中漂浮着一块冰,在水的表面上又覆盖着一层油。已知水面高度h1,油面高度h2,则当冰熔化之后( )
A.水面高度h1升高,油面高度h2升高
B.水面高度h1升高,油面高度h2降低
C.水面高度h1降低,油面高度h2升高
D.水面高度h1降低,油面高度h2降低
展开答案
【答案】B
【解答】解:①假设把冰分成二部分,一份的浮力等于水产生的浮力,它化成水后,保持液面不变;另一份的浮力由油产生,它化成水后将使油面下降。但使原来的水面上升;
②油对冰产生浮力,油层的一部分是冰排开油多占的体积,冰化成水后,水的量增多了,水面上升,但是油没有增多,并且失去了冰所占的一部分体积,体积减小,油面下降。
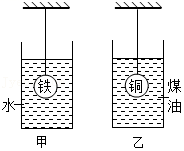
如图所示,在图甲中,用细线将一实心铁球浸没在水中静止,图乙中将一实心铜球浸没在煤油中静止。铁球所受重力为G铁;体积为
V铁;铜球所受重力为G铜,体积为V铜。铁球和铜球所受细线的拉力大小相等,所受浮力分别为F铁和F铜,已知水的密度为ρ水,煤油的密度为ρ油,且ρ油<ρ水<ρ铁<ρ铜,则下列判断正确的是( )
A.V铜=V铁 B.V铜>V铁 C.F铜=F铁 D.F铜<F铁
展开答案
【答案】D
【解答】铁球的拉力
$F=m_铁g-\rho_水\dfrac{m_铁}{\rho_铁}g$
$F=m_铜g-\rho_油\dfrac{m_铜}{\rho_铜}g$
所以选D
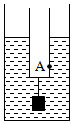
如图所示,容器内有水,有一塑料试管下面挂一小铁块,浮在水面上。现将小铁块取下放入试管中,试管仍浮在水面,则( )
A.液面上升
B.液面下降
C.容器底部受到液体的压强不变
D.试管外壁上A点受到液体的压强不变
展开答案
故选:C
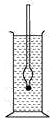
如图所示,小东让一密度计漂浮在水面上,然后往水中加适量食盐,下列说法中正确的是( )
A.密度计会上浮一些
B.液体对容器底部的压强变小
C.漂浮时密度计受到的浮力大于重力
D.密度计静止时,液体对它的浮力变小
展开答案
【解答】解:
因为加食盐前后,密度计都漂浮,自重不变,
所以密度计受到的浮力不变,F浮=G,故CD错误;
因为F浮=ρ液V排g,液体的密度增大,
所以密度计排开水的体积减小,将上浮一些,故A正确;
因为p=ρgh,液体的密度增大,h不变,
液体对容器底的压强变大,故B错误。
故选:A。
如图所示,弹簧秤下用细线系一个高为0.2m的金属圆柱体,静止悬停在空的圆柱形水槽中,水槽的底面积为0.12m2,水槽上方有一水龙头,开启水龙头,水匀速注入水槽时开始计时,直到水槽水满溢出为止,金属圆柱体始终保持静止,弹簧秤的示数与时间的关系图线如图2所示,g=10N/kg,水的密度ρ水=1.0×103kg/m3,试根据图中数据,求:
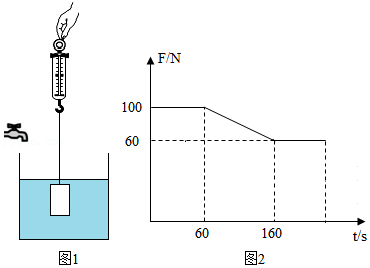
(1)金属的密度。
(2)金属圆柱体的底面积。
(3)水龙头每秒流出的水的体积。
(4)试画出槽内的水对底的压强p随时间t变化的图像,并在图像中标注特殊点的坐标数值。
展开答案
【答案】答:(1)金属的密度为2.5×103kg/m3;
(2)金属圆柱体的底面积为2×10﹣2m2;
(3)水龙头每秒流出水的体积为2×10﹣4m3;
(4)槽内的水对底的压强p随时间t变化的图像如上所示。
将一个密度小于甲、乙两种液体的木块分别放在两种液体中,当两种液体的密度之比是4:5,则木块静止时排开两种液体体积之比是( )
A.1:1 B.4:5 C.5:4 D.2:1
展开答案
【解答】解:因为木块的密度小于液体的密度,所以在两种液体中都漂浮,浮力等于重力,即F浮甲=F浮乙
因为F浮=ρgV排,
所以木块静止时排开两种液体体积之比,故C正确。
质量相等的两个实心小球甲和乙,已知它们的密度之比是ρ甲:ρ乙=1:3,现将甲、乙两球放入盛有足够多水的烧杯中,当甲、乙两球处于静止状态时,水对两球的浮力之比F甲:F乙=3:2,下列结论中错误的是( )
A.甲球受到的浮力与它的重力相等
B.甲球漂浮,乙球沉底
C.甲乙两球都漂浮
D.甲球的密度为0.5×103kg/m3
展开答案
【解答】解:因为两球质量相等,密度之比是ρ甲:ρ乙=1:3,体积之比为V甲:V乙=3:1,
若两球在水中都漂浮,就有F甲:F乙=G甲:G乙=m甲:m乙=1:1,与实际不符,显然不是都漂浮,故C错误;
若两球在水中都是全部浸没,就有F甲:F乙=ρ水gV甲:ρ水gV乙=V甲:V乙=3:1,与实际不符,显然不可能是全部浸没;
由此判断:只有是一个漂浮、一个浸没;由于它们的密度之比是ρ甲:ρ乙=1:3,所以只能是甲球漂浮,乙球下沉,故B正确;
甲球漂浮,浮力等于重力,故A正确;
则F甲:F乙=ρ甲V甲g:ρ水V乙g=ρ甲V甲:ρ水V乙=3:2,
所以$\rho=\dfrac{s\rho_水V_乙}{2V_甲}=\dfrac{3×1.0x10^3kg/m^3×1}{2×3}=0.5×103kg/m3$,故D正确。
故选:C。
如图甲所示,一弹簧下端固定在容器的底部,上端与一个重为20N的正方体相连,此时水的深度为0.2m,弹簧的伸长量为4cm。在弹性限度内,弹簧产生的弹力F与其伸长量x之间的关系如图乙所示。(g取10N/kg,ρ水=1.0×103kg/m3)求:
(1)正方体的质量;
(2)水对容器底部的压强;
(3)正方体浸在水中的体积。
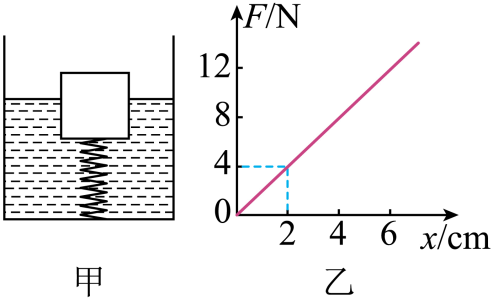
展开答案
【答案】(1) 2kg; (2) 2×10³Pa; (3) 2.8×10⁻³m³
【解析】(1) 正方体的质量
$m = \frac{G}{g} = \frac{20N}{10N/kg} = 2kg$
(2) 水对容器底部的压强
$p = \rho_{水}gh = 1.0×10³kg/m³ × 10N/kg × 0.2m = 2×10³Pa$
(3) 由图乙,当弹簧的伸长量为4cm时,弹簧产生的弹力F为8N,则正方体所受的浮力
$F_{浮} = G + F = 20N + 8N = 28N$
正方体浸在水中的体积
$V_{排} = \frac{F_{浮}}{\rho_{水}g} = \frac{28N}{1.0×10³kg/m³ × 10N/kg} = 2.8×10⁻³m³$
如图所示,有一重为6N,边长为0.1m的实心正方体木块A放在水平桌面上,一个底面积为0.02m2的薄壁圆柱形容器放在水平桌面中央(容器足够高),内盛有0.3m深的水。若把木块放入圆柱形容器里的水中,若要木块A恰能完全浸没在水中,则要在木块上加竖直向下的压力F为_______ N;从漂浮到刚好完全浸没的过程中木块的重力做功_______ J。
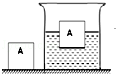
展开答案
【解答】解:(1)木块完全浸没在水中时受到的浮力F浮=ρ水gV排=ρ水gV=1×103kg/m3×10N/kg×(0.1m)3=10N,
在木块上增加的压力F=F浮﹣G=10N﹣6N=4N;
- 木块漂浮时F浮1=G=6N,则:$V_{排1}=\dfrac{F_{浮1}}{\rho_水g}=\dfrac{6N}{1.0X10^3KG/M^3X10N/kg}=6×10^-4m^3$
露出的木块高度
$h’=L-\dfrac{V_{排1}}{S{木块}}=0.1-\dfrac{6×10^{-4}m^3}{(0.1)^2}=0.04m$木块从漂浮到完全浸没在水中的过程中,木块下降的距离:
$h=h’-\dfrac{\Delta V{排}}{S}=0.04-\dfrac{(0.1m)^3-0.6×10{-4}m^3}{0.02m^2}=0.02$
该过程中重力做的功W=Gh=6N×0.02m=0.12J。
故答案为:4;0.12。
如图所示,一个底面积为2m2的圆柱状容器,装有适量的水,现在将一个体积为5m3的长方体物体A放入其中,最终物体漂浮于水面上。现在将虚线以上的部分截取走(截走部分的体积等于露出水面体积的一半),待剩余部分再次静止后水面下降了0.3m。则:
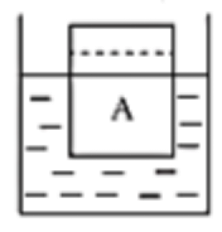
(1)容器底部受到的压强减少了多少?
(2)容器底部受到的压力减少了多少?
(3)物体A的密度为多少?
展开答案
【答案】(1)3×10³Pa;(2)6×10³ N;(3)0.4×10³kg/m³或0.6×10³kg/m³
【解析】(1)容器底部受到的压强减少量
∧p = ρgh = 1×10³ kg/m³ × 10N/kg × 0.3m = 3×10³Pa
(2)容器底部受到的压力减少量
△F = △P/S = 3×10³Pa × 2m² = 6×10³N
(3)截取走那部分物体的重力
G = △F = 6×10³N
截取走那部分物体的质量
$m = \frac{G}{g} = \frac{6 \times 10^3 N}{10 N/kg} = 600 kg$
物体处于漂浮状态,浮力等于重力,即
$F_{浮} = G$
$\rho_{水} g V_{排} = \rho g V$
$V_{排} = \frac{\rho}{\rho_{水}} V$
截走部分的体积等于露出水面体积的一半,所以
$V_{截} = \frac{1}{2} (V – V_{排}) = \frac{1}{2} (V – \frac{\rho}{\rho_{水}} V)$
$m = \rho V_{截} = \rho \times \frac{1}{2} V (1 – \frac{\rho}{\rho_{水}})$
$600 kg = \rho \times \frac{1}{2} \times 5 m^3 (1 – \frac{\rho}{1 \times 10^3 kg/m^3})$
$\rho = 0.4 \times 10^3 kg/m^3$ 或 $\rho = 0.6 \times 10^3 kg/m^3$
圆柱形容器的底面积为200cm2,容器中水的深度为8cm,将一实心圆柱体A放入容器中 ,液面上升了2cm,如图所示,再缓慢向容器中注水,当注入1.28kg水时,圆柱体A对容器的压强恰好为零,(g=10N/kg, ρ水=1.0×103kg/m3) 求
(1)圆柱体A的底面积?
(2)求圆柱体A的质量?
(3)再将圆柱体A竖直向上提升8cm ,求水对容器底压强的变化量?
展开答案
(1)由题意知,放入物体后水面上升了\(\Delta h = 2\mathrm{cm}=0.02\mathrm{m}\),此时物体浸没在水中的深度为\(h_{浸}=10\mathrm{cm} = 0.1\mathrm{m}\),因为\(S_{物}h_{浸}=S_{容}\Delta h\),则\(S_{容}=\frac{S_{物}h_{浸}}{\Delta h}\),
代入已知数据可得\(S_{容}=40\mathrm{cm}^{2}=4.0\times 10^{-3}\mathrm{m}^{2}\)。
(2)当注入\(m_{注水}=1.28\mathrm{g}=1.28\times 10^{-3}\mathrm{kg}\)水时,在物体离开容器底之前水应从物体的两侧上升,设重新注入水后水面上升的深度为\(\Delta h_{2}\),
由\(m_{注水}=\rho_{水}(S_{容}-S_{物})\Delta h_{2}\)(\(\rho_{水}=1.0\times 10^{3}\mathrm{kg}/\mathrm{m}^{3}\))
代入上述数据可得:\(\Delta h_{2} = 8\mathrm{cm}=0.08\mathrm{m}\)
则此时物体浸没在水中的深度为\(h_{水}=18\mathrm{cm}=0.18\mathrm{m}\)。
又因为此时圆柱体\(A\)对容器的压强恰好为零,所以\(F_{浮}=G_{物}\),即\(\rho_{水}gS_{物}h_{水}=mg\)(\(g = 10\mathrm{N}/\mathrm{kg}\)),
代入已知数值可得\(m_{物}=720\mathrm{g}=0.72\mathrm{kg}\)。
(3)再将圆柱体\(A\)竖直向上提升\(h_{升}=8\mathrm{cm}=0.08\mathrm{m}\),则水只从两侧下降,此时物体减小的排开液体体积\(V_{排}=S_{物}h_{升} = 320\mathrm{cm}^{3}=3.2\times 10^{-4}\mathrm{m}^{3}\)。
因为水只从两侧下降,所以此时水面下降的深度\(\Delta h_{3}=\frac{V_{排}}{S_{容}-S_{物}}=\frac{3.2\times 10^{-4}\mathrm{m}^{3}}{(4.0\times 10^{-3}\mathrm{m}^{2}-S_{物})}\),可得水面下降的深度\(\Delta h_{3}=2\mathrm{cm}=0.02\mathrm{m}\)。
所以水对容器底压强的变化量\(\Delta P=\rho_{水}g\Delta h_{3}=1.0\times 10^{3}\mathrm{kg}/\mathrm{m}^{3}\times 10\mathrm{N}/\mathrm{kg}\times 0.02\mathrm{m}=200\mathrm{Pa}\)。
如图所示,甲、乙两个实心小球, 体积分别为V甲、V乙,密度分别为ρ甲、ρ乙, 质量分别为m甲、m乙, 两个容器A、B中装有密度分别为ρ1、ρ2的液体, 已知它们的密度关系为ρ1<ρ甲<ρ乙<ρ2, 则( )
A. 若V甲=V乙, 将甲、乙都放入容器A中, 静止时二者所受浮力之比为ρ甲: ρ乙
B. 若V甲=V乙, 将甲、乙都放入容器B中, 静止时二者所受浮力之比为ρ1: ρ2
C. 若m甲=m乙, 将甲、乙都放入容器B中, 静止时二者所受浮力之比为ρ乙: ρ甲
D. 若m甲=m乙, 将甲、乙分别放入容器A、B中, 静止时二者所受浮力之比为ρ1: ρ甲
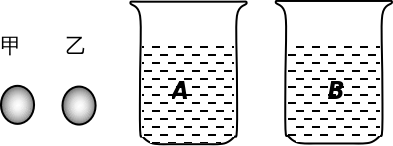
展开答案
【答案】D
如图所示, 将重为G的金属小球用细线系好, 浸入盛水的烧杯中(烧杯中的水没有溢出), 金属小球受到的浮力为F浮, 杯底增加的压力为△F1; 如将此金属小球直接投入水中, 杯底增加的压力为△F2, 则下列关系式中正确的是( )
A. △F2-△F1= F浮
B. △F2+△F1= G
C. △F2∶△F1= G ∶F浮
D. △F2∶△F1=F浮∶G
展开答案
【答案】C
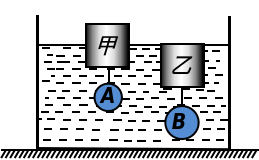
A和B是密度为ρ=5×103kg/m3的某种合金制成的两个小球, A球的质量为mA=100g; 甲和乙是两个完全相同的木块, 其质量为m甲=m乙=320g, 若用细线把球和木块系住, 则在水中平衡时如图所示, 甲有一半体积露出水面, 乙浸没水中(g取10N/kg),则下列计算正确的是( )
A. 木块的密度为0.6×103 kg /m3
B. 如果剪断木块乙和B球之间的细线, B球静止后, 所受重力和浮力的合力的大小为4.8N
C. 如果剪断木块乙和B球之间的细线, 乙木块露出水面的体积为4.6×10-4m3
D. 如果剪断木块甲和A球之间的细线, A球静止后, 所受重力和浮力的合力为0.2N
展开答案
【答案】B
$\dfrac{V_甲}{2}+V_A=320+100$
$V_甲=800$
所以密度为0.4
