测量例题
随着5G信号的快速发展,5G无人物品派送车已应用于实际生活中,图甲所示为无人物品派送车沿直线路径前往派送点的情景。该车从出发点到达派送点,完成任务后返回出发位置,其行驶路程s与所用时间t的关系如图乙所示。下列分析正确的是( )
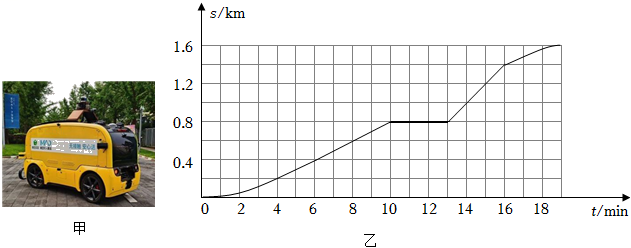
A.从派送点返回出发点用时19min
B.派送点到出发点的距离为1.6km
C.0~10min内派送车的平均速度为0.08km/min
D.10~13min内派送车做匀速直线运动
展开答案
【答案】C
【解答】解:A、从派送点返回出发点用时为19min﹣13min=6min,故A错误;
B、派送点到出发点的距离为1.6km﹣0.8km=0.8km,故B错误;
C、0~10min内派送车的平均速度为:$V=\dfrac{S}{t}=\dfrac{0.8km}{10min}=0.08km/min$,故C正确;
D、10~13min内,根据图像平行t轴,派送车静止不动,故D错误。
在某校举办的机器人模拟救援比赛中,甲、乙两机器人同时从同一地点出发,沿直线匀速运动到10m远的目的地,它们运动的路程随时间变化的图像如图所示。下列说法正确的是( )
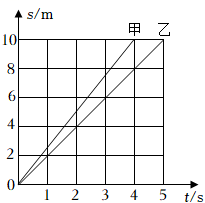
A.甲的速度大小为4m/s B.乙的速度大小为2m/s
C.甲的运动时间比乙多1s D.甲的运动时间比乙少2s
展开答案
【答案】B
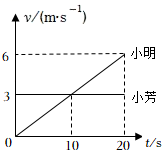
周日做完作业,小明和小芳同学在风景如画的柳叶湖畔骑自行车,如图所示是他们在某段路面上的速度随时间变化的图像。下列分析中错误的是( )
A.0~10s两人所通过的路程相等
B.以湖畔的垂柳为参照物,小芳总是运动的
C.第10s末,两人的速度相等
D.小芳做匀速直线运动
展开答案
【答案】A
2022年5月10日,天舟四号货运飞船与空间站组合体完成自动交会对接,如图所示,货运飞船与空间站对接完成后,下列说法正确的是( )

A.货运飞船相对于空间站是运动的
B.货运飞船和空间站相对于地球是运动的
C.货运飞船相对于地球是静止的,空间站相对于地球是运动的
D.货运飞船相对于地球是运动的,空间站相对于地球是静止的
展开答案
【答案】B
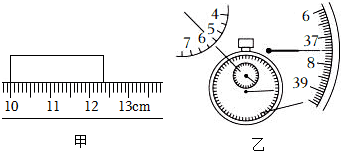
(2022•苏州模拟)如图甲所示刻度尺的分度值是_______cm,物体A的长度是 _______cm;如图乙所示,停表的读数为 _______s。
展开答案
【答案】0.1;2.35;337.5。
【解答】解:(1)由图甲知:刻度尺1cm之间有10个小格,所以1个小格代表的是0.1cm,即此刻度尺的分度值为1mm;木块左端与10.00cm对齐,右端与12.35cm对齐,所以木块的长度为L=12.35cm﹣10.00cm=2.35cm;
(2)停表小盘的分度值是0.5min,指针在5min和6min之间,偏过中线;大盘的分度值是0.1s,而大盘指针在37.5s,因此停表读数为5min37.5s=337.5s。
甲、乙两个学生从桥头走到大桥$\dfrac{1}{3}$处时,忽听背后火车鸣笛,甲转身向后以6m/s的速度跑到桥头,此时火车刚好上桥,而乙则是以6m/s的速度向前跑向另一桥头,当火车刚好上桥时,乙距离另一桥头的路程是 ________ L(L为桥长),当乙到达另一桥头时,火车刚好追上他,则火车的速度是 ______ m/s。
展开答案
【答案】$\dfrac{1}{3}$;18。
【解答】解:根据题意可知当火车刚好上桥时,乙距离另一桥头的路程为$\dfrac{1}{3}$L;
火车经过大桥所用时间等于乙跑完$\dfrac{1}{3}$L路程所用时间,
根据$t=\dfrac{s}{v}$,
则根据题意可得:$\dfrac{\dfrac{1}{3}L}{6m/s}=\dfrac{L}{V}$
则火车的速度$v=\dfrac{6m/s \times L}{\dfrac{1}{3}L}=18m/s$
“频闪照相”是研究物体运动时常用的一种实验方法,照相机每隔相等的时间曝光一次,记录下物体的位置。甲、乙两个小球均从位置a竖直下落到位置b,其各自的频闪照片如图所示,试根据照片分析:
(1)甲、乙从位置a竖直下落到位置b,平均速度之比为 ________
(2)若甲球的重量为mg,受到空气阻力与速度的关系$f=kv$(k为常数),则甲球下落过程中可达到的最大速度为v=_______(写出表达式)
展开答案
【答案】(1)5:3;(2)$\dfrac{mg}{k}$
【解答】解:(1)假设从位置a竖直下落到位置b的路程为s,两次曝光相隔的时间为t,
则甲小球所用的时间t甲=3t,乙小球所用的时间t乙=5t,
甲、乙两球的平均速度之比:$\dfrac{v_甲}{v_乙}=\dfrac{\dfrac{s}{3t}}{\dfrac{s}{5t}}=\dfrac{5}{3}$
(2)当匀速下落时,甲球达到的最大速度,
因为$G=f$
又有已知,$f=kv$,
所以,$G=kv=mg$,
故得甲球的下落速度:$v=\dfrac{mg}{k}$
下列单位换算过程中正确的是( )
A.6.5km=6.5×1000=6500m B.6.5km=6.5 km×1000=6500m
C.6.5km=6.5 km×1000m=6500m D.6.5km=6.5×1000m=6500m
展开答案
【答案】D
【解析】本题根据长度单位的进率进行换算.换算的步骤为:原来的数字、乘号、进率、后来的单位、最终结果.
油分子很小,在一般的电子显微镜下是看不到的,其直径最接近的答案是 ( )
A、1$u$m B、10 nm C、0.1 nm D、0. 01 nm
汽车向放置在路边的测速仪匀速驶来,测速仪向汽车发出两次短促的(超声波)信号,如图所示,从第一次发出信号到测速仪接收到信号用时0.5s,从第二次发出信号到接收到信号用时0.3s,若两次发出信号的时间间隔是0.9s,求:
(1)汽车接收到第一次信号时距测速仪多少米?
(2)汽车的速度为多少?(超声波的速度是340m/s)
展开答案
【答案】
(1)汽车接收到第一次信号时距测速仪为85米;
(2)汽车的速度是42.5m/s。
【解答】解:
(1)由速度公式$v=st$
得测速仪第一次发出的信号从汽车处返回到测速仪时,汽车距测速仪:s1=v声t1=340m/s×0.25s=85m;
(2)第二次发出的信号从汽车处返回到测速仪时,汽车距测速仪:s2=v声t2=340m/s×0.15s=51m;
因此汽车在两次与信号相遇的过程中行驶了:s′=s1-s2=85m-51m=34m;
这34m共用了:t′=△t-t12+t22=0.9s-0.25s+0.15s=0.8s,
所以汽车的车速为:v′=s′t′=34m0.8s=42.5m/s。
近几年,国家取消了7座及以下小车在法定长假期间的高速公路收费,给自驾出行带来了很大的实惠,但车辆的增多也给道路的畅通增加了压力,因此交通部门规定,上述车辆通过收费站口时,在专用车道上可以不停车交卡而直接减速通过,已知物体做匀变速直线运动时路程和时间的关系式为$s=v_0+\dfrac{1}{2}at^2$,其中$v_0$表示物体的初始速度,a称为加速度,表示物体单位时间内速度的变化量,即$a=\dfrac{v_1-v_0}{t}$,若某车减速前进的速度为$v_0=72km/h$,通过2.4s到达收费站,到达收费站口的速度为$v_1=28.8km/h$,然后立即以$a=4m/s^2$的加速度加速至原来的速度(假设收费站的前、后都是平直大道)。试问:
(1)小车减速前的行驶速度72km/h=______m/s;
(2)若驾驶员在到达收费站之前,均匀减速,则在此过程中的加速度为多少?
(3)该车从收费站口开始加速,经过多长时间速度能达到减速之前的速度?
(4)交通管理部门为了交通安全,特制定了死亡加速度500g(g取10m/s2)这一数值以警世人,意思是如果行车加速度达到此值,将有生命危险。若两辆摩托车以36km/h的速度相向而行发生碰撞,碰撞时间为2×10﹣3s,试判断一下驾驶员是否有生命危险?
展开答案
【答案】
【解答】解:(1)$72km/h=72 \times \dfrac{1000m}{3600m/s}=20m/s$
(2)初速度v0=20 m/s,末速度$v_1=28.8 km/h= \times \dfrac{1000m}{3600m/s}=8 m/s$,
所以到达收费站之前的这段路程中,加速度为:$a_1=\dfrac{v_1-v_0}{t}=\dfrac{8m/s-20m/s}{2.4s}=-5m/s^2$
(3)小车通过收费站时的速度为v1=8 m/s,以a=4m/s2的加速度开始加速,则速度到达20m/s所需要的时间:
$t’=\dfrac{v_0’-V_1}{a}=\dfrac{20m/s-8m/s}{4m/s^2}=3s$
- 摩托车发生碰撞后做减速运动,初速度
$v_0’’=36km/h=36 \times \dfrac{1000m}{3600m/s}=10m/s$,末速度为$v_1″=0 m/s$,时间$t″=2×10^3s$,则加速度为:
$a’’=\dfrac{v_1’’-V_0’’}{t’’}=\dfrac{0m/s-10m/s}{2×10^{-3}s}=-5000g$
度数值达到了500g,因此驾驶员有生命危险。
(1)20;
(2)若驾驶员在到达收费站之前,均匀减速,则在此过程中的加速度为﹣5m/s2;
(3)该车从收费站口开始加速,经过3s速度能达到减速之前的速度;
(4)驾驶员有生命危险。
