wk12

水桶实验

如果用长绳吊一水桶，让它旋转至绳扭紧，然后将水注入，水与桶都暂处于静止之中

2022年8月23日 No Comments

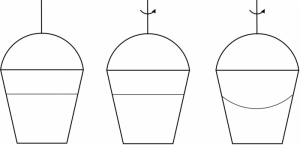
如图所示，一个质量为M长为L的圆管竖直放置，顶端塞有一个质量为m的弹性小球，M=4m，球和管间的滑动摩擦力和最大静摩擦力大小均为4mg．管从下端离地面距离为H处自由落下，运动过程中，管始终保持竖直，每次落地后向上弹起的速度与落地时速度大小相等，不计空气阻力，重力加速度为g．求：（1）管第一次落地弹起时管和球的加速度；（2）管第一次落地弹起后，若球没有从管中滑出，则球与管达到相同速度时，管上升的最大高度。（3）管第二次弹起后球不致滑落，L应满足什么条件．（1）管第一次落地弹起时，管瞬间向上运动，受到自身重力以及摩擦力，所以管的加速度 $a_{1} = \frac{4 m g + 4 m g}{4 m} = 2 g$ 方向向下。球受到向上的摩擦力和向下的重力，球加速度 $a_{2} = \frac{f - m g}{m} = \frac{4 m g - m g}{m} = 3 g$ 方向向上。（2）取竖直向下为正方向．球与管第一次碰地时速度 $v_{0} = \sqrt{2 g H}$ ，方向向下．碰地后管的速度 $v_{1} = - \sqrt{2 g H}$ ，方向向上；球的速度 $v_{2} = \sqrt{2 g H}$ ，方向向下若球刚好没有从管中滑出，设经过时间 $t_{1}$ ，球管速度v相同，则有 $- v_{1} + a_{1} t_{1} = v_{2} - a_{2} {t_{1}}^{2}$ $- \sqrt{2 g H} - 2 g t_{1} = \sqrt{2 g H} + 3 m g t_{1}$ $2 \sqrt{2 g H} = 5 m g t_{1}$ $t_{1} = \frac{2}{5} \sqrt{\frac{2 H}{g}}$ 此时管下端的高度为 $h_{1} = v_{0} t_{1} - \frac{1}{2} a_{1} {t_{1}}^{2}$ 带入数据 $h_{1} = \frac{12}{25} H$ 此后管和球共速上升 $v_{g} = v_{0} - a_{2} t_{1} = \frac{1}{5} \sqrt{2 g H}$ 共速上升的高度 $h_{2} = \frac{v_{g}^{2}}{2 g} = \frac{1}{25} H$ 管上升的最大高度 $H_{1}$ $H_{1} = h_{1} + h_{2} = \frac{13}{25} H$ （3）设第一次弹起过程中球相对于管的位移 $x_{1}$ ，在管开始下落到上升到 $H_{1}$ 的过程中，由动能减少量等于摩擦力做功 $M g (H - H_{1} + m g (H - h_{1} + x_{1}) - 4 m g x_{1} = 0$ $x_{1} = \frac{4}{5} H_{1}$ 即L应满足条件 $x_{1} + x_{2} \leq L$ $\frac{4}{5} H + \frac{4}{5} H_{1} \leq L$ $$\frac{4}{5}H +\frac{4}{5}

2022年8月23日 No Comments

人物

吴健雄——世界物理女王

吴健雄是世界一流物理学家，她是20世纪华人妇女的杰出代表

2022年8月14日 No Comments

李哥考题输入专用

这是一个实例 $$ 美元符号中间就是公式， \frac{1}{2} j就会变成 $\frac{1}{2}$ <?php echo do_shortcode(‘[pdf id=”3227″]’); ?>

2022年8月12日 No Comments

人物

伟人杨振宁，不是诺贝尔奖给他荣光，而是他给诺贝尔奖荣光！

是继爱因斯坦和狄拉克之后，20世纪物理学最卓越的设计师（弗里曼·戴森语）。

2022年8月5日 No Comments

实验

埃拉托色尼测量地球圆周

你只要学会一种诞生于2000多年前的酷炫的测量方法，就可以在几分钟内完成这个惊人的实验

2022年7月26日 No Comments

考试

一道看似简单的动量题.

如图所示，一高h=1.25m、质量 $m_{b} = 2 k g$ 的木块B，在一水平向右的恒力F=3N作用下，在水平地面上向右运动。现将一质量 $m_{a} = 1 k g$ （可视为质点）的小滑块A轻轻静置（相对地面的速度为零）于木块B上距B左端b=1.00m的水平面上，一段时间后A从B上滑落，A刚离开B的时刻，B向右运动的距离 $x_{0} = 1.5 m$ ，已知A与B间的动摩擦因数，B与水平地面间的动摩擦因数均为μ=0.10， $g = 10 m / s^{2}$ （结果均保留2位有效数字）。说明：这是一个看似简单的题目，但是大多数学生都不能完全作对，分析来分析去，第一、我们对动量的直觉不够敏感，把那种对相等力的冲量直觉变成准确的直觉。第二担心自己的计算力，这需要隔三差五就练习一遍，并没有所谓的天才都是孰能生巧，聪明的人会敢于挑战，不聪明的直接放弃。解析过程简单的分析a、b的受力可以得到各自的加速度，然后用加速和时间去算，发现有太多未知量，只能放弃。 $u (m_{a} + m_{b}) g = 3 N$ $0.1 (1 k g + 2 k g) 10 m / s^{2} = 3 N$ 当a放到b上，b的摩擦力始终和恒力大小相等方向相反，所以恒力对b速度的影响不变。所以ab相对滑动的过程整体动量守恒，这样就可以降低难度了。数据： $m_{a} = 1 k g$ 、 $x_{0} = 1.5 m$ 、 μ=0.10 、b=1m、 F=3N、 $x_{0} = 1.5 m$ 假设： $v_{0}$ 是b的碰撞的初始速度， $v_{b}$ 是ab分离时b的速度。 $x_{a}$ 是a相对于地面的位移， $x_{0} = 1.5 m$ 是b相对于地面的位移 a的方程式 $m_{b} v_{0} = m_{b} v_{b} + m_{a} v_{a}$ …… ① $u m_{a} g x_{a} = \frac{1}{2} m_{a} v_{a}^{2}$ ……② $u m_{a} g x_{0} = \frac{1}{2} m_{b} v_{0}^{2} - \frac{1}{2} m_{b} v_{b}^{2}$ …..③ $x_{a} = x_{0} - b$ …….④ 方程列好后，别着急计算，检查一遍，看看字母有没有带错，数据有没有问题，各个物理量之间的关系对不对，我就理解错了 $x_{a}$ 的意思，浪费了很多时间。然后找最容易下手的地方去计算。先从 $x_{a} = x_{0} - b$ ，这里下手，发现 $x_{a} = 0.5 m$ 带入方程②，得到 $u m_{a} g x_{a} = \frac{1}{2} m_{a} v_{a}^{2}$ ，$0.1\times10